蒙特卡罗法(卷名：自动控制与系统工程)
monte-carlo method
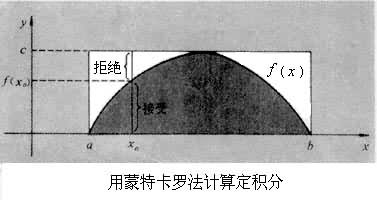
通过构造概率模型并对它进行随机试验来解算数学问题的方法。以计算函数f(x)的定积分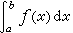
为例（见图），首先构造一个概率模型:取一个边长分别为c和b-a的矩形,并在矩形内随机投点,假设随机点均匀地落在整个矩形之内,则落在图中阴影区内的随机点数n与投点总数N之比 n/N，就近似地等于阴影区面积与矩形面积之比：
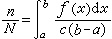。由此可求出定积分
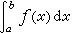。蒙特卡罗法历史悠久。1773年法国G.-L.L.von布丰曾通过随机投针试验来确定圆周率π的近似值，这就是应用这个方法的最早例子。蒙特卡罗是摩纳哥著名赌城，1945年 J.von诺伊曼等人用它来命名此法，沿用至今。数字计算机的发展为大规模的随机试验提供了有效工具，遂使蒙特卡罗法得到广泛应用。在连续系统和离散事件系统的仿真中，通常构造一个和系统特性相近似的概率模型，并对它进行随机试验，因此蒙特卡罗法也是系统仿真方法之一。
蒙特卡罗法的步骤是：①构造实际问题的概率模型；②根据概率模型的特点，设计和使用降低方差的各类方法，加速试验的收敛；③给出概率模型中各种不同分布随机变量的抽样方法；④统计试验结果，给出问题的解和精度估计。
概率模型 用概率统计的方法对实际问题或系统作出的一种数学描述。例如对离散事件系统中临时实体的到达时间、永久实体的服务时间的描述（见离散事件系统仿真方法）就是采用概率模型。虽然由这些模型所确定的到达时间、服务时间可能与具体某一段时间内实际到达时间、服务时间有出入，但它是通过多次统计获得的结果，所以从概率分布的规律来说还是相符的。概率模型不仅可用来描述本身就具有随机特性的问题或系统，也可用来描述一个确定型问题。例如参数寻优中的随机搜索法（见动力学系统参数寻优）就是将参数最优化问题构造为一个概率模型，然后用随机投点、统计分析的方法来进行搜索。
随机数的产生 用蒙特卡罗法进行仿真时，需要应用各种不同分布的随机变量。只要有一种连续分布的随机变量，就可设法得到任意分布的随机变量。在(0，1)上均匀的分布函数是一种最简单的连续分布函数。因此在
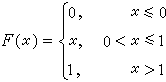蒙特卡罗法中，多是先产生均匀分布随机变量 R的抽样值ri(i＝1，2，…),称为随机数。在计算机中产生随机数的方法有：①把已有的随机数表输入计算机；②用物理方法，如噪声型随机数发生器产生出真正的随机数；③用数学方法根据递推公式
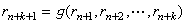由程序来产生。这种方法速度高，占用机器的内存少，使用最为普遍。在计算机中表示一个数字的字长有限，因此只能表示有限个不同的数，而且用递推方法产生的数值序列{rn}是完全确定的，到一定长度便周而复始，这些都与随机数的基本性质相矛盾。但是只要产生的数值序列{rn}能够通过随机数的各种统计检验，仍可以把它当作随机数来使用。为区别起见，常将用数学方法产生的随机数称为伪随机数。