计算几何(卷名：数学)
computational geometry
由函数逼近论、微分几何学、代数几何、计算数学等形成的新兴边缘学科，它研究几何外形信息的计算机表示、分析和综合。它是计算机辅助几何设计(即CAGD)这门技术的数学基础。从20世纪60年代起，计算机辅助设计和辅助制造开始进入造船、航空和汽车工业的产品几何外形设计和制造领域中。设计者首先需要把一般的曲线或曲面的外形表示在计算机上，然后对这些曲线或曲面的几何性质进行分析，看曲线上有无拐点、奇点，曲面是不是凸的，等等，最后提出一种有效的数值方法，由程序或由人机对话控制这些曲线和曲面的形状，使其符合设计要求。
在70年代，主要用的计算几何图形是：贝济埃曲线和曲面、B样条曲线和曲面、孔斯曲面等。
1962年起，法国雷诺汽车公司的工程师P.E.贝济埃以逼近为基础，开始构造参数曲线表示法，完成了一种自由型曲线和曲面的设计系统“UNISURF”，并于1972年在雷诺汽车公司正式投入使用。n次贝济埃曲线的数字表示式是n次参数曲线段
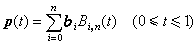， (1)式中
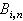(t)为二项分布密度，其表达式为
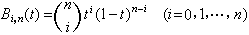；n+1个向量{bi}是由设计者事先给定的，它们的终点组成了所谓贝济埃特征多边形的顶点。函数族{
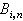(t)}也称为n次伯恩斯坦基函数族，因此，式(1)的p(t)可理解为对于贝济埃特征多边形{bi}的向量值的伯恩斯坦逼近。平面上的三次贝济埃曲线是最常用的，它们的形状如图1
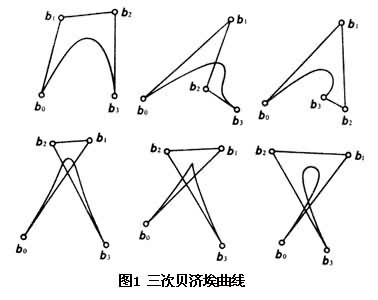所示。当设计者需要修改曲线时，只要稍微调整特征多边形的某几个顶点位置，对应曲线的形状便会随之变动，但仍保留对特征多边形的逼近性质。1972～1974年期间，在贝济埃用多边形控制曲线形状的方法的启发下，人们把多项式B样条函数（见样条函数）扩张为参数形式的B样条曲线，并使用B样条特征多边形来控制它。其中最有用的是三次式和二次式。同 B样条曲线贝济埃曲线相比较，除了直观和保凸这些共有的优点外，还具有下列几个优点：①局部修改只影响邻近几段函数，不会牵一而动百；②对特征多边形逼近得更好，且便于控制；③B样条多项式的次数低，计算简单；④样条上允许出现直线段和某些折角，适应范围更广。由于这些优点，B样条曲线在几何外形设计中很有前途。图2
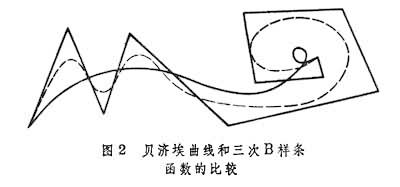是数控绘图机绘制的贝济埃曲线(实线)和三次B样条曲线（虚线），它们对应于同一个特征多边形，可见后者逼近得更好。1964～1967年，S.A.孔斯构造了一种用四边曲面片的阵列来表示曲面的方式。其中，工程中最常用的是双三次孔斯曲面片，它的矩阵表示式为
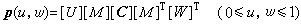， (2)式中上标T代表矩阵的转置，矩阵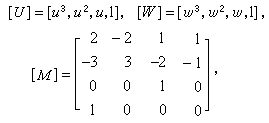
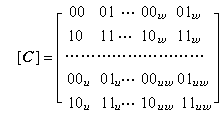。[C]称为角点信息矩阵，它的每个元素都是向量，矩阵分成四块。左上角代表四个角点的位置向量。左下角和右上角分别表示边界曲线在四个角点处沿u方向和w方向的切向量。这三块就惟一决定了四条边界曲线的形状。右下角称为角点“扭矢”，调整扭矢会引起曲面片内部的隆伏，而对曲面边界不发生影响（图3
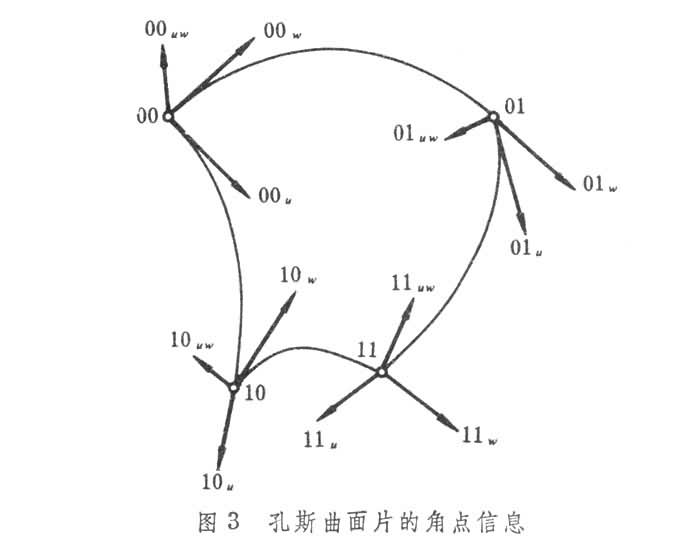）。把上述小片的孔斯曲面片拼起来，使得连接处达到一阶或二阶偏导数连续，便能构造各种复杂形状的几何外形。它们在飞机外形设计中有很多应用。
贝济埃曲线和B样条曲线可通过直积的形式而拓广成为曲面表示。最常用的是双三次形式。在式(2)中，取
，
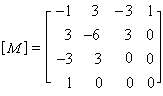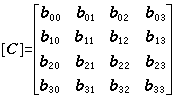，便得到双三次贝济埃曲面片的表示式。这时，矩阵[C]称为特征网格。设计者可以通过调整它来实现对曲面片形状的控制（图4
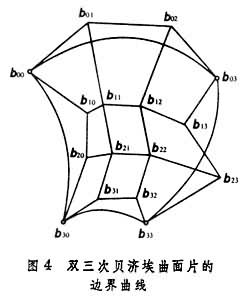）。B样条曲面也具有类似的表示式。双三次的孔斯曲面、贝济埃曲面和B样条曲面，都是双三次参数曲面的特殊情形。三者还能够通过非异线性变换而相互转化，它们在数学上是等价的。然而，从应用的角度看，这三种曲面各有所长，而且适用于不同的课题。
参考书目
苏步青、刘鼎元著：《计算几何》，上海科学技术出版社，上海，1981。
I.Barnhill and R.F.Riesenfeld， ed.，Computer Aided Geometric Design，Academic Press， New York，1974.
I.D.Faux and M.J.Pratt，Computational Geometryfor Design and Manufacture，John Wiley & Sons，New York， 1979.