运算放大器(卷名：电子学与计算机)
operational amplifier
能对信号进行数学运算的放大电路。它曾是模拟计算机的基础部件，因而得名。采用集成电路工艺制做的运算放大器，除保持了原有的很高的增益和输入阻抗的特点之外，还具有精巧、廉价和可灵活使用等优点，因而在有源滤波器、开关电容电路、数-模和模-数转换器、直流信号放大、波形的产生和变换，以及信号处理等方面得到十分广泛的应用。
运算放大器的电路结构有三种主要形式。一是单端输入、单端输出，斩波稳定式直流放大器等采取这种形式。二是差分输入、单端输出，大多数集成运算放大器采取这种形式。三是差分输入、差分输出，直流放大器和部分集成放大器采取这种形式。
频率补偿 运算放大器是多级放大电路，通常在较高的频率上仍具有大于1的增益，而内部电路产生的附加相移却已达到或超过180°。因而，在反馈运用条件下会产生自激振荡。采用频率补偿，即采用附加电容、附加电阻等元件可减小相移，使放大器稳定。最常用的补偿方法是单极点补偿。它是在高增益中间放大级加反馈电容。频率补偿所用的电容应满足下述条件：
Cf≥gm/2πfu (1)式中gm是差动输入级的跨导，fu是放大器的稳定单位增益频带宽度。对于通用型运算放大器来说，fu约为1兆赫，gm通常设计得很小，例如200微欧，补偿电容只需要数十皮法，它可以和放大器制做在同一芯片上。
大信号响应 在大的输入信号脉冲驱动下，运算放大器的输出电压随时间变化的最大速率称为电压摆率，通常用符号SR表示。因为差动输入级被驱动到饱和状态时，它提供给补偿电容的充电电流与允许的放电电流不能超过输入级偏置电流I
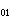，因此SR＝I
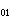/Cf (2)大多数运算放大器的电压摆率在1伏／微秒以下，然而在某些改进的设计中电压摆率已达到100伏／微秒以上。理想运算放大器 开环增益A和输入阻抗Ri均趋近于无穷大、输出阻抗Ro趋近于零的运算放大器。这是用于电路分析的一种概念。采用理想运算放大器这一概念可以使电路分析简化。例如，在含有运算放大器的图1a电路中，假定差分输入端的电压为uε，放大后的输出电压由负反馈电阻Rf反馈回输入端。若放大器的增益为无穷大，则必定迫使相消后的输入电压uε为零。这个物理现象通常称为虚短路特性。因此，对于含有理想运算放大器的电路，可以假定差分输入端的电压和电流均为零，输入阻抗力无穷大。因为实际的运算放大器，其直流增益通常在104倍以上，差分输入电阻为兆欧量级。因此，利用理想运算放大器作为近似条件，对于低频率电路（如模拟运算器）的分析来说其结果与实际情况基本符合。
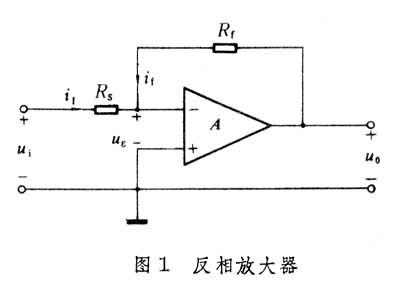
放大运用的基本电路 运算放大器常被用来实现电信号的反相放大、同相放大和差分输入／输出放大。引入反馈很容易控制其放大倍数。对于图1的反相放大器电路，利用虚短路特性可以写出i1=ui/Rs，if＝-u0/Rf。由于放大器输入电流为零，故i1＝if，于是可求得电压增益
这表明放大器增益只决定于电阻Rf/Rs的比值。
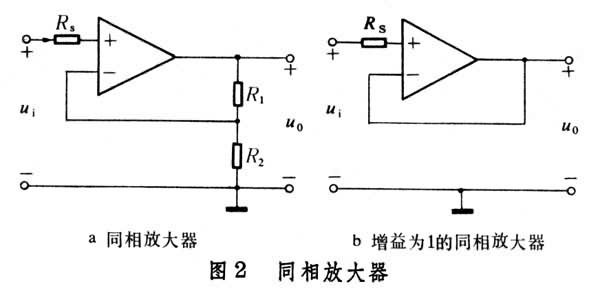
图2a中同相放大器电路的电压增益为
图2b是图2a在R1=0时的情况。这时R2是多余的，整个放大器变成一个跟随器，其电压增益K＝1。
在模拟计算机中，相加和积分是两种基本运算。它们都能用运算放大器电路来实现。
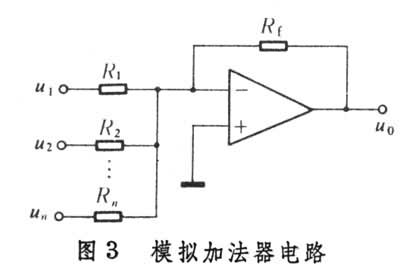
① 模拟加法器:图3是模拟加法器的电路。利用理想运算放大器的近似条件可得到
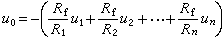(5)若取R1＝R2＝…＝Rn＝Rf，就可得到简单的求和关系式
u0＝-(u1+u2+…+un) (6)
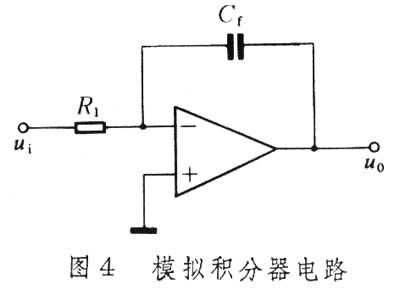
② 模拟积分器:图4是模拟积分器电路。假定电容器Cf上起始电压是零，由虚短路特性可知，i1＝ui/R1＝if。又u0＝-uc＝-1/Cf
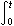ifdt。于是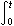uidt (7)若Cf起始电压不为零，式(5)还要附加一个起始电压。
实际的运算放大器 在许多应用中，理想运算放大器的近似分析常常不够精确。实际运算放大器的增益是有限值，而且随频率的升高而降低;其输入阻抗不是无穷大，输出阻抗也不等于零。这些都会引起模拟运算误差并限制运算放大器的使用频率。作为直流放大单元，运算放大器的零点漂移、输出动态范围、差分输入的失调电压、失调电流和共模抑制比，以及输出电压的最大变化率等技术指标，都会影响运用效果。这些因素在实际应用中须加以考虑。
参考书目
J.K.Roberge，Operational Amplifier Theory and Practice，Wiley，New York，1975.