随体导数(卷名：力学)
material derivative
流体质点在欧拉场内（见流体运动学）运动时所具有的物理量对时间的全导数。如果取流体质点的速度矢量v(r，t)为物理量，则加速度
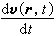就是速度矢量的随体导数，式中r为质点的位置矢量；t为时间。根据复合函数微分法则，可得：
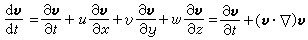，式中
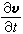称为速度矢量的局部导数或当地导数;u、v、w为v在直角坐标系中的三个分量；(v·墷)v称为速度矢量的位变导数或对流导数。于是，随体导数等于局部导数和位变导数之和。用算符 
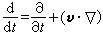可推广上式来表示其他物理量的随体导数。如果取密度为质点的物理量，则密度的随体导数为
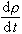。质点的密度在运动过程中不变的流体称为不可压缩流体。因此，对于不可压缩流体而言，有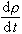=0。