随机积分(卷名：数学)
stochastic integral
对某些随机过程类适当定义的各种积分的总称。它们在随机过程与随机微分方程的研究和应用中各有其重要的作用。
伊藤积分 这是对布朗运动定义的一种随机积分。布朗运动的样本函数虽然连续，但几乎所有的样本函数非有界变差，甚至处处不可微，因而无法按样本函数来定义通常的黎曼－斯蒂尔杰斯积分（简称RS积分）或勒贝格-斯蒂尔杰斯积分（简称LS积分）。一般来说，RS积分定义中的达布和不会以概率1收敛到一定的极限，但在适当的条件下，达布和的均方极限存在。伊藤清正是利用这一性质定义了对布朗运动的随机积分。设{
，t∈R+=[0，∞)}是一族上升的子σ域，布朗运动W＝{W(t)，t∈R+}是()鞅。如果样本连续的有界随机过程φ＝{φ(t)，t∈R+}是()适应的，那么当有限区间[α，b]嶅R+的分割
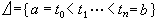的直径
趋于零时，达布和 
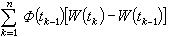的均方极限存在，记作
，它称为φ在区间[α，b]上对W 的伊藤积分。值得注意的是，在达布和的构造中，被积过程在[tk-1，tk]上的取值点不是随意一点，而只能是它的左端点 tk-1。这是一个严格的限制。完全不加限制时其极限不存在，如作其他的限制，则可能得到另外的极限，从而定义出另外的积分，但最有用的是这种限制。伊藤积分最重要的性质是著名的伊藤公式:设F是二次连续可微的实函数，则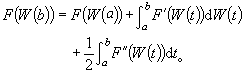
这一公式及其各种推广在理论上和应用上都有重要的作用。例如，可以用来证明关于布朗运动的鞅刻画的莱维定理：一个从零出发的样本连续过程W={W(t)，t∈R+}为布朗运动的充要条件，是W 和{W 2(t)-t，t∈R+}都为鞅。对平方可积鞅的随机积分 使E
的鞅x＝{x(t)，t∈R+}称为平方可积鞅，其中x(∞)是当t→∞时，x(t)以概率1 收敛的极限。对一个平方可积鞅x， -x2是类(D)上鞅，因此根据上鞅分解定理，x 2可惟一地表成一致可积鞅M和可料增过程A 之和， X 2(t)＝M(t)+A(t)。由此，对任何样本连续的有界适应过程 φ，当［α，b)］的分割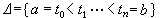
的直径δ(墹)趋于零时，达布和
的均方极限存在，这个极限就称为φ 在[α，b)]上对x的随机积分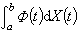
。这种积分也有相应的伊藤公式：对二次连续可微的函数F，
右边最后一项是按轨道的LS积分，可料增过程A的轨道是右连续增函数。这种随机积分还可以进一步推广到对局部鞅以至半鞅的积分。斯特拉托诺维奇积分 在伊藤积分定义的达布和中，如果用在小区间[tk-1，tk]中点的被积过程值φ
(或者等价地， 用在两个区间端点的过程值的算术平均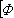
代替左端点的过程值φ(tk-1)，则均方极限也存在，但此极限与伊藤积分不相同，它定义了用斯特拉托诺维奇命名的另一种积分，记作
这种积分的一个优点是，对一个三次连续可微的函数F，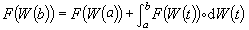
，它保持了普通微积分中牛顿-莱布尼茨公式的形式。其他类型的随机积分 常见的还有均方随机积分和对正交增量过程的积分。对一个均方连续的随机过程x，即对一切t0∈R+满足
的x，达布和
的均方极限存在，它定义了x在区间[α，b)]上的均方随机积分，记作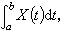
其中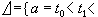
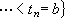是[α，b]的分割，sk可在[tk-1，tk]上任取，均方极限是在δ(墹)趋于零的条件下取的。设Z 是一个正交增量过程，即对一切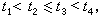
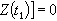那么对任一［α，b］上的连续函数ƒ，达布和
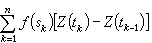的均方极限定义了ƒ在［α，b］上对Z的积分，记作
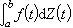。这种对正交增量过程积分的最重要的应用是宽平稳过程的谱表示（见平稳过程）。随机微分方程 形如
的方程称为伊藤方程，其中α(s，x)、σ(s，x)是一次连续可微的二元函数，W是布朗运动，X是待求的半鞅。由于形式上还可以将方程改写为 dx（t）＝α(t，x(t))dt+σ(t，x(t))dW(t)这种微分表示，习惯上常称为(伊藤)随机微分方程。理论上对它已有很多研究，解的存在惟一性问题已经解决，并且有各种形式的推广，如用半鞅代替布朗运动等。但能把解明确表达出来的还只有少数简单的特例，如对x(0)=1，α(s，x)呏0，σ(s，x)呏x，方程
有惟一解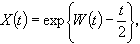
它是一个样本连续鞅。此外，对于均值函数为零的实二阶过程x(见随机过程)，可定义其各阶均方导数。若x的协方差函数 Г(s，t)＝Ex(s)x(t)二次连续可微，则差商[x(t+Δt)-x(t)]/Δt当 Δt→0 时的均方极限总存在，它定义了x的一阶均方导数
。一般地，若 Г(s，t)2n次连续可微，则x的n阶均方导数存在。联系着一个二阶过程x及其各阶均方导数之间的方程，如
等，称为均方随机微分方程。求解它，就是要找出满足该关系式的二阶过程x。例如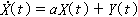
在初值x(0)=ξ下的惟一解是
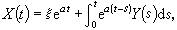其中α是实常数，ξ为已知的随机变量，Y为已知的均方连续随机过程，而积分是均方随机积分。参考书目
J.L.Doob，Stochastic Processes，John Wiley & Sons.New York， 1953.
严加安编著：《鞅与随机积分引论》，上海科学技术出版社，上海，1981。