高分子溶液(卷名：化学)
polymer solution
指高聚物溶解在溶剂中形成的溶液。在高分子科学发展的早期，由于溶液中高分子的尺寸大小与胶体粒子的大小相似，因此高分子溶液曾一度被错误地认为是一种胶体溶液，后来很多实验证明高分子溶液是处在热力学平衡状态的真溶液，而且是能用热力学函数来描述的分子分散的稳定体系。研究高分子稀溶液的性质可以得到高分子的分子量与分子量分布、高分子在溶液中的形态和尺寸大小以及高分子与溶剂分子间相互作用等重要参数。高分子的极稀溶液的减阻作用在流体力学方面得到实际应用。高分子浓溶液在合成纤维生产中的溶液纺丝、干法纺丝，片基生产中的溶液铸膜，塑料的增塑等都有密切的关系。这方面的研究侧重在高分子溶液的流变性能与成型工艺的关系。高分子溶液的混合热、混合熵和混合自由能等热力学性质的研究和高分子在溶液中的迁移性质（包括高分子溶液的沉降、扩散和粘度）的研究都是高分子溶液基础研究的重要方面。
高聚物的溶解过程 高聚物的溶解比小分子化合物慢得多。溶解过程分为两个阶段：①高聚物的溶胀，由于非晶高聚物的分子链段的堆砌比较松散，分子间的作用力又弱，溶剂分子比较容易渗入非晶高聚物内部，使高聚物体积膨胀；而非极性的结晶高聚物的晶区分子链堆砌紧密，溶剂分子不易渗入，只有将温度升高到结晶的熔点附近，才能使结晶转变为非晶态，溶解过程得以进行。在室温下，极性的结晶高聚物能溶解在极性溶剂中。②高分子分散，即以分子形式分散到溶剂中去形成均匀的高分子溶液。交联高聚物只能溶胀，不能溶解，溶胀度随交联度的增加而减小。
高分子溶液（特别是那些溶剂的溶解能力较差的溶液）在降低温度时往往会发生相分离，分成两相，一相是浓相；另一相为稀相。浓相的粘度较大但仍能流动；稀相比分级前的浓度更低。往高分子溶液中滴加沉淀剂也能产生相分离，高分子的相分离有分子量依赖性，因而可以用逐步沉淀法来对高聚物进行分子量的分级。
高分子在溶剂中溶解度的判定 在一定程度上仍可用极性相近原则来判定高分子的溶解度，即极性大的高聚物溶于极性大的溶剂，反之亦然。更精确一点的方法是通过比较高聚物和溶剂的溶度参数 δ，溶度参数δ 的定义是内聚能密度的平方根，它是物质凝聚态分子间相互作用能的一种量度。当高聚物和溶剂的溶度参数的差值Δδ 较大时(Δδ＝|δp－δS|，δp为高聚物的溶度参数，δS为溶剂的溶度参数)，高分子就不易溶于溶剂中；如果高聚物与溶剂的溶度参数极为接近，则高分子容易溶于溶剂中。粗略地从目前实验得到的数据来看，对非极性溶剂来说，可以发生溶解的最大允许的Δδ 值约为±0.8，对极性溶剂来说约为±3.4。由于分子间的相互作用和溶解过程比较复杂，因此用溶度参数来判定溶解性能仍有例外情况（见高聚物内聚能密度）。
高分子溶液理论 目前比较重要的高分子溶液理论有以下几种：
弗洛里－哈金斯晶格理论 尺寸和形状都相同的小分子混合物与理想溶液的偏离常归因于混合热的存在；但是溶液性质的非理想性也可由于分子尺寸有较大差别所造成。对高分子溶液而言，一个长链高分子的分子体积远大于溶剂分子体积，而且链段间的键接使链段在晶格上的排布有一定的相关性。1942年P.J.弗洛里和M.L.哈金斯假定链段与溶剂分子具有相同的体积，都占有一个晶格点（图1），
然后各自独立地计算了n1个溶剂分子和n2个由x个链段连接而成的高分子在空间格子中的可区分的构象排布数目，导得构象混合熵ΔSm：ΔSm＝－k(n1ln φ1＋n2ln φ2)式中φ1和φ2分别为溶剂和高分子的体积分数；k为玻耳兹曼常数。 体系的混合热ΔHm等于形成一个链段－溶剂接触点所需的能量Δε乘以接触点的数目：
ΔHm＝ZΔεn1φ2＝kTχn1φ2式中Z为晶格配位数；T为绝对温度；χ＝ZΔε/kT，称作相互作用参数，又称弗洛里－哈金斯参数。由此可得到混合自由能ΔGm：
ΔGm＝kT(n1ln φ1＋n2ln φ2＋χn1φ2)并进一步导得各组分的偏摩尔混合自由能与各种溶液性质的理论关系。
在弗洛里－哈金斯的晶格理论中，相互作用参数χ是高分子－溶剂体系中溶剂能力的量度，溶剂愈良，χ值愈小。χ值随温度的降低而单调上升，降低温度会产生相分离，从而能说明上临界溶解温度的存在。晶格理论对临界相分离条件和高分子在两相中分配的分子量和浓度依赖性所作的分析与实验事实基本相符，从而为高聚物的分级条件的选择以及在分级数据的处理上提供了理论依据。
虽然弗洛里－哈金斯的晶格理论在高分子科学的发展上起了重要作用，但理论本身仍存在一些缺点，它无法说明在ΔHm=0的高分子溶液体系中χ值并不是零，也无法说明从渗透压的第二维利系数（又译维里系数）A2＝
得到的χ值有分子量的依赖性，式中Μ1为溶剂的分子量；ρ1、ρ2为溶剂和高聚物的密度。从量热学测定ΔHm时得到的χ值，有高分子浓度的依赖性。另一方面，高分子溶解时常伴随有体积的改变，还发现升高温度也能产生相分离，即存在一个下临界溶解温度（图2）。对于这些事实，晶格理论也都没有预计到。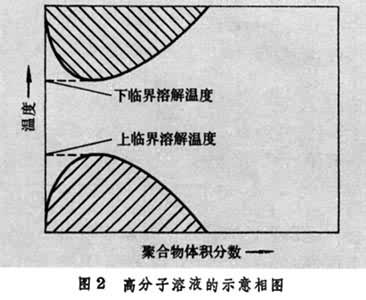
稀溶液理论 弗洛里－哈金斯理论的晶格模型忽略了一个实际问题，即在很稀的高分子溶液中，链段的空间分布必然是非连续的，在高分子线团所在的区域链段的浓度很高，而在高分子线团之间却为纯溶剂所占据。高分子的每一个链段都占有一定的体积，在此体积中排除了其他链段进入的可能，通常称为排除体积效应，它又依赖于溶剂的性质。在良溶剂中，高分子链段优先选择溶剂分子作为近邻，使高分子的实际尺寸和排除体积增大。相反地，在劣溶剂中排除体积却减小。排除体积的理论计算是一个十分复杂的问题，但可以预期它应与相互作用参数χ有关。1950年弗洛里和W.R.克里格鲍姆假定高分子线团在溶液中近似球形，其中链段密度按高斯函数的形式分布。他们计算了高分子稀溶液的热力学函数，并提出了一个具有温度量纲的参数 θ（常称为弗洛里温度）。在T＝θ时，高分子溶液的热力学性质与理想溶液的偏差消失。 θ点可以用改变溶液的温度或改变溶剂的性质而达到。高分子在θ 溶剂中的尺寸相当于高分子链的链段间没有相斥和相吸引力时的尺寸，常称为无扰尺寸，此时，第二维利系数A2为零。
状态方程理论 弗洛里－哈金斯晶格理论保留了小分子正规溶液理论的主要特点，只是对相应的混合熵作了修正，以适应高分子的特殊性。它还假定混合时没有体积变化，这些都与实际情况不符。
对应态原理说明，一对分子i和j之间的位能ε(rij)与它们之间的距离rij有关，它可以用一个普遍适用的位能函数Φ表示为：
式中ε*和r*是反映分子结构的特征参数，分别具有能量和长度的量纲。从这两个特征参数，又可以定义无量纲的对比温度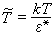
，对比体积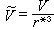
和对比压力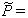
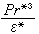这三个对比变量，将这些变量引入统计热力学的配分函数，即可得到状态方程
，其具体形式只依赖于位能函数Φ的本质。在二元混合物中，各不同组分间的相互作用可用
六个特征参数描述。假设它们依从同一形式的位能函数 Φ，则可导得混合物的第二维利系数和混合时的体积变化。在原则上，从实验数据可以计算相异组分间的相互作用，但在实际上直接计算ε*和r*还是困难的，需要借助于各种简化了的模型。状态方程理论应用于混合物时，其最大的成功在于它能说明混合时体积的改变，这一改变在两个组分的分子尺寸和相互作用差别较大时更为显著，过量体积常为负值。状态方程理论应用于高分子溶液时，可以正确地预计相互作用参数χ 的浓度依赖性并解释下临界溶解温度的存在。
标度理论 把铁磁体在居里点附近的相变理论应用于高分子链构象的处理。当铁磁体冷到居里点温度TC以下时，在没有外磁场下，从整体说没有磁矩，但在局部区域也有磁矩。与原子自旋取向相关的局部磁区的大小，即相关尺寸ξ的温度依赖性为：
式中τ为对比温度；v为一个特征幂数，此式在τ →0时成立。这个关系与一个孤立的柔性链高分子在良溶剂中的均方半径
随聚合度N 变化的情况相似，即
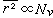。与铁磁体相变理论的类比，可得出在d维晶格上的有排除体积效应的无规行走应符合v＝3/(d+2)的结论。在三维时，v＝3/5。标度理论只能得到两个量之间的标度关系，即其中一个量增大一倍时另一个量应增大多少倍的问题，也即找出幂数关系的数值。标度理论也适合于处理柔性链高分子浓溶液。对于良溶剂，目前已经得出的重要结论是:浓溶液渗透压
，式中c 是浓度；线团的均方半径随浓度的变化应服从 
的规律。但这些结果还有待更多的实验验证。参考书目
黄子卿著：《非电解质溶液理论导论》，科学出版社，北京，1973。
H. Yamakawa，Modern Theory of Polymer Solution，Harper & Row， New York， 1971.