分圆域(卷名：数学)
cyclotomic field
添加单位根到有理数域上而生成的扩域。
1847年，E.E.库默尔宣称他证明了费马猜想，在证明中，将费马方程
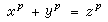（p为奇素数）在环
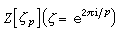中分解成
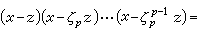
，并认为环Z[ζp]与通常有理数环Z一样，每个数都可惟一地表成一些“素数”的乘积。但不久发现他的这个看法是错误的，例如在Z[ζ23]中就存在表示成一些“素数”的乘积的方式不是惟一的这种数。于是库默尔创造了“理想数”这一概念来弥补他的证明中的缺陷，并对分圆域的特性作了深刻的研究。库默尔关于分圆域的工作和C.F.高斯关于二次域的工作，是代数数论的两个源头。J.W.R.戴德金将“理想数”系统化而产生了抽象代数中的“理想”这一重要概念。所谓分圆域，是指在有理数域Q上添加n次本原单位根
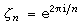（即复平面上单位圆的n 等分点）而得到的数域K=Q(ζn)。由于当n呏2(mod4)时Q(ζn)=Q(ζn/2)，从而可假定n扝2(mod 4)。和二次域一样，分圆域中的许多数论特性也比较简单，例如：对于分圆域K=Q(ζn)，K/Q是φ(n)次伽罗瓦扩张，其中φ(n)是欧拉函数，而伽罗瓦群Gal(K/Q)={σα｜1≤α≤n，(α，n)=1}，其中自同构σα是由
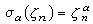所决定的，于是Gal(K/Q)同构于乘法群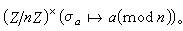
K=Q(ζn)的整数环为Z[ζn]，而判别式为
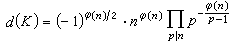。素数p在分圆域K=Q(ζn)中分解规律为：若P凲n，则p为OK=Z[ζn]中g个不同素理想之积，并且每个素理想的剩余次数均是ƒ，其中ƒ为p对于模 n的阶数（即ƒ为满足pƒ呏1(mod n)的最小正整数），而g =φ(n)/ƒ。若p│n，令
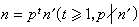，则
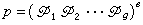，其中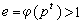
（从而p在K中分歧），
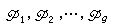是OK中g个不同的素理想，其剩余次数均为ƒ，ƒ为p对于模n′的阶数，而
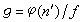。分圆域K=Q(ζn)的单位根群WK，是由ζl生成的l阶循环群，其中l=n(当(n呏0(mod 4)时)或者l=2n（当n呏1(mod2)时）。
分圆域K=Q(ζn)的单位群UK是单位根群WK和VK的直积，其中VK是由
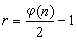个单位ε1，ε2，…，εr生成的（乘法）自由阿贝尔群，即K中每个单位均可惟一地表示成
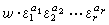，其中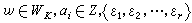
称为分圆域K的一个基本单位组，寻求分圆域的基本单位组是一个困难的问题。和二次域一样，分圆域的类数也具有解析的计算公式，但是在公式中包含基本单位组的知识，这使得关于分圆域类数的研究和计算成为困难问题。
库默尔关于分圆域的最重要工作，有以下几方面：
对于每个奇素数p，如果p除不尽分圆域 Q(ζp)的类数hp，那么费马方程
没有整数解（x，y，z），xyz≠0（例如在100以内，满足p|hp的只有P=37、59、67，从而对于不超过100的其他21个奇素数p，费马方程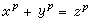
均没有正整数解）。以h
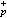表示域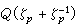
(这是Q(ζp)的极大实子域)的类数，则h
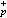｜hp，即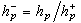
为整数，并且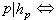
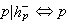除尽伯努利数B2，B4，…，Bp-3之中某个的分子
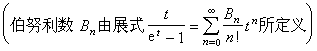。通过大量的手算，库默尔发现了当p→+∞ 时，h
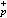变化不大，而hр则飞速地增长。他猜想:
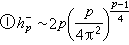（当P→+∞时）;
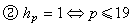。后一猜想由K.乌希达于1971年和J.马斯利、H.L.蒙哥马利各自独立地证明了，H.蒙哥马利还证明了对于正整数n扝2(mod 4)则类数为1的分圆域Q(ζn)共有29个，即n=3，4，5，7，8，9，11，12，13 15，16，17，19，20，21，24，25，27，28，32，33，35，36，40，44，45，48，60，84。前一猜想则至今未能解决。继库默尔之后，德国数学家H.哈塞对于分圆域以及一般阿贝尔数域的类数问题作了相当精细的研究。他于1952年所著《关于阿贝尔域的类数》就是他的这些研究工作的总结。
现代分圆域理论的创始人是岩泽健吉。基于深刻的代数思想和与代数曲线算术理论的类比，他于1959年得到一类数公式：设
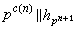(其中pc(n)‖m表示pc(n)|m，而pl+1凲m)，则存在与n无关的常数μp、λp和vp，使得当n充分大时， 
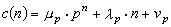。他对于更一般的情形也证明了类似的公式，例如，对每个代数数域K，令hn是
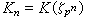的类数，pc(n)‖hn，则存在与n无关的常数 μp(K)，λp(K)和vp(K)，使得当n充分大时，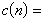
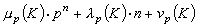。岩泽健吉猜想:对于每个数域K均有μp(K)=0。他的两个学生B.费雷罗和L.C.华盛顿于1978年对于阿贝尔数域K证明了这个猜想，但对于其他数域还未完全解决。岩泽健吉还猜想：对于任意全实域K均有λp(K)=0。这个猜想甚至对于实二次域也未能完全解决。如果l/K是数域的伽罗瓦扩张，并且它的伽罗瓦群是阿贝尔群，那么l称为K的阿贝尔扩张。如果K是有理数域Q的阿贝尔扩张，那么K称为阿贝尔数域。从伽罗瓦理论可知，分圆域的每个子域都是阿贝尔数域。反之，每个阿贝尔数域也必是某个分圆域Q(ζn)的子域，其等价说法是：
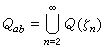是Q的极大阿贝尔扩域，这就是著名的韦伯-克罗内克定理。对于希尔伯特第12问题:能否对任意的代数数域K 明显地构作出K的全部阿贝尔扩张？或者说，能否明显地刻画出K的极大阿贝尔扩域？韦伯-克罗内克定理给出了关于K=Q情形的答案。Qab 是对Q 添加指数函数(这是单周期函数)
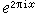在全部有理点x∈Q处的值而得到的域。1853年，20岁的L.克罗内克猜想：每个虚二次域K的极大阿贝尔扩域是将 K添加某种椭圆函数（这是双周期函数）在全部有理点处的取值而得到的域。这就是所谓的克罗内克青春之梦。在1920年高木贞治创立了类域论之后，克罗内克猜想得到了证明，但是对于其他类型的代数数域，希尔伯特第12问题离完全解决还相距甚远。
分圆域的理论是代数数论中一个在不断发展的课题。它与模形式理论、代数几何（特别是椭圆曲线的算术理论）、代数K理论、p进分析等交织在一起，形成当前很活跃的数学领域。
参考书目
S.Lang，Cyclotomic Fields， Vol.1～2，Springer-Verlag.New York，1978，1980.
L. C. Washington，Introduction to Cyclotomic Fields，Springer-Verlag，New York，1982.