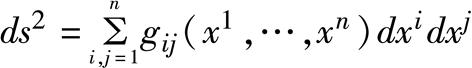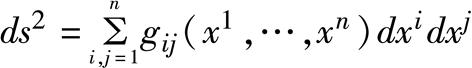出处：数理化力学卷 • 数 学 • 几何 • 拓扑
黎曼几何
黎曼几何 几何学的分科。对n维空间中任意两个无限邻近的点都给定了距离,具体地说,点(x1 ,…,x n )和点(x1 +dx1 ,…,x n +dx n )之间的距离可表为 其中系数矩阵(g ij )是正定的。称ds2 为黎曼度量,g ij 为黎曼度量张量的分量。这种空间中的每一小片都近似于欧几里得空间,但总体上却能反映出空间的弯曲的性质。1854年黎曼首先提出了这样的几何学,后称“黎曼几何”。随着广义相对论的建立,它已成为微分几何的基础,也是微分方程、变分法、拓扑学等数学分支所需要的研究工具。20世纪后期黎曼几何的研究主要集中在对黎曼几何的整体性质的研究,即研究黎曼几何的各种几何量(如黎曼曲率、黎奇曲率、数量曲率等)与空间的拓扑性质之间的关系。有时非欧几里得几何中的椭圆几何也被称为“黎曼几何”。