词条	数学期望
释义	数学期望 天文学地球科学卷 数学期望 　　　　概率论中描述随机变量分布集中程度的一个数字特征。是随机变量X的取值x1,x2,…,xn与其概率P1,P2,…,Pn的乘积和$\stackrel{n}{\underset{i=1}{\mathrm{\Sigma }}}$Pixi。符号以E(X)表示。是随机变量取值的理论平均值。在测绘学的测量数据处理中,当测量数据仅带有偶然误差时数学期望或理论平均值视为测量数据或观测值的真值。 出处：天文学地球科学卷 • 测　绘　学 • 大地测量学 • 测量平差 哲学卷 数学期望　　亦称“均值”。概率论的基本概念。指随机变量ξ的平均值。常记为Eξ。它描写了随机变量的取值中心。例如,Eξ=8表示随机变量ξ所取的值大多在8的周围。在测量工作中,由于偶然误差的数学期望为零,观测量的数学期望为其真值,因此,常以观测值的平均值作为未知数学期望的估计值。 出处：哲学卷 • 逻　辑　学 • 现代形式逻辑 数理化力学卷 数学期望　　简称“期望”,亦称“均值”。随机变量ξ取值的加权平均数,其权就是相应的概率或概率密度。常记为Eξ。例如,随机变量ξ取值x1,x2,…,x n,其概率分别为p1,p2,…,p n,则其加权平均数p1x1+p2x2+…+p nx n就是ξ的数学期望。数学期望由其概率分布唯一确定,故亦称某分布的数学期望。它表征了概率分布的中心位置。例如,Eξ=8表示随机变量ξ所取的值大多在8的周围。在测量工作中,由于偶然误差的数学期望为零,观测量的数学期望为其真值,因此,常以观测值的平均值作为未知数学期望的估计值。 出处：数理化力学卷 • 数　　学 • 概率论 • 数理统计 管理学卷 数学期望 　　　　亦称“均值”。(1)当随机变量X为离散型时,设其可能的取值为x1,x2,…,相应的概率分别为p1,p2,…,若级数 　　绝对收敛,则称它为X的数学期望或均值,记为 　　。 　　　　(2)当随机变量X为连续型时,设其概率密度函数为p(x),若积分绝对收敛,则称它为X的数学期望或均值,记为。　　当|x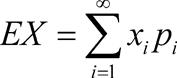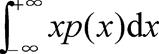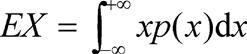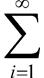i|pi或者|x|p(x)dx发散时,则称X的数学期望不存在。数学期望由概率分布唯一确定,故亦称为分布的数学期望,它表征了随机变量取值的加权平均。例如,EX=8表示随机变量X所取的值大多在8的周围。在测量工作中,由于测量误差的数学期望为0,观测量的数学期望为其真值,因此常以观测值的平均值作为未知数学期望的估计值。 出处：管理学卷 • 统　计　学 • 概率论 心理卷 数学期望（mathematical expectation）　　亦称“期望”、“均值”。随机变量最基本数学特征之一。反映随机变量平均取值的大小，是简单算术平均的一种推广，类似加权平均。 出处：心理卷 • 心理统计与测量 • 心理统计 • 描述统计
随便看	马哈瓦尔制 马哈福兹 马哈穆德·喀什噶尔 马哈茂德·喀什噶里 马哈茂德·楚拉斯 马哈赞加 马唐 马喇 马嘉人 马嘉理事件 马嘉理案 马嘎尔尼 马嚼子 马国翰 马图什卡 马图林 马图里迪 马图里迪学派 马圆线虫病 马场坪 马场马术 马坊使 马坚 马坝人 马坦巴王国

百科全书收录258893条中英文百科知识，基本涵盖了大多数领域的百科知识，是一部内容开放、自由的电子版百科全书。