出处:教育卷 • 教育原理 • 教育统计学
相关系数
相关系数(correlation coefficient) 统计分析中度量不同变量间关联程度和方向的统计指标。用r表示。相关系数的取值范围一般为(-1,+1)。相关系数的绝对值越接近于1,表示两个变量之间联系程度越大。相关系数小于0时,称为负相关;大于0时,称为正相关;等于0时,称为零相关。依据相关现象之间的不同特征,统计指标的名称亦有所不同。如将反映两变量间线性相关关系的统计指标称为线性相关系数(相关系数的平方称为决定系数或判定系数);反映两变量间曲线相关关系的统计指标称为非线性相关系数;将反映多元线性相关关系的统计指标称为复相关系数等。
相关系数 表示两个现象之间相关程度的统计分析指标。计算公式为:
r=
其中xi 为自变量的标志值,i=1,2,…n,
为自变量的平均值,为因变量数列的标志值,y为因变量数列的平均值。相关系数(r)数值范围在-1和+1之间,其绝对值越大,相关程度越高。一般划分为:
r=
其中x
出处:政治学社会学卷 • 社 会 学 • 社会学方法 • 概念 术语
相关系数 概率论中表示两个随机变量ξ和η之间线性联系程度的一个量,其绝对值总在0和1之间。ξ和η之间的线性联系程度愈大,相关系数的绝对值就愈接近于1。当ξ和η满足线性关系式aξ+bη=c时,相关系数的绝对值为1;当ξ和η的变化为同一方向时,相关系数为正,反之为负。通常在得到(ξ,η)的n组观察值(x1 ,y1 ),(x2 ,y2 ),n ,y n )后,可用下式中的样本相关系数r来估计ξ与η的相关系数: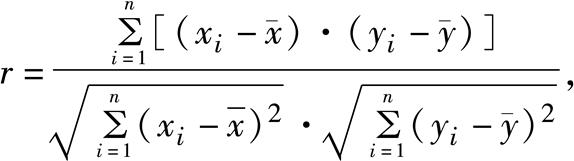 其中、分别为{x
其中、分别为{xi }、{yi }的算术平均值。
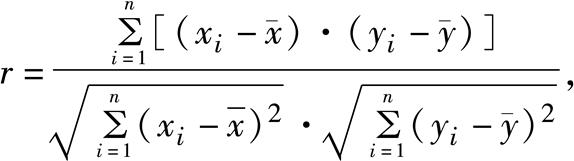
出处:数理化力学卷 • 数 学 • 概率论 • 数理统计
相关系数
设随机变量X、Y的方差分别为var(X)、var(Y),且均不等于0,X与Y的协方差为cov(X,Y),则称
为X、Y的相关系数,记为ρXY 。它是反映随机变量X和Y之间线性联系程度的数字特征,它的值介于-1和1之间。X和Y之间的线性联系程度越大,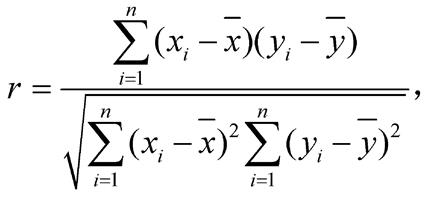 就越接近于1。其中=1的充分必要条件为以概率1成立线性关系式aX+bY=c,其中a、b、c为常数;当X和Y的变化同方向时,相关系数为正,反之为负。通常在得到(X,Y)的n组观察值(x
就越接近于1。其中=1的充分必要条件为以概率1成立线性关系式aX+bY=c,其中a、b、c为常数;当X和Y的变化同方向时,相关系数为正,反之为负。通常在得到(X,Y)的n组观察值(x1 ,y1 ),…,(xn ,yn )后,可用下式中的r来估计相关系数ρXY :,分别为{xi }和{yi }的算术平均值。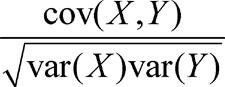
设随机变量X、Y的方差分别为var(X)、var(Y),且均不等于0,X与Y的协方差为cov(X,Y),则称
为X、Y的相关系数,记为ρ
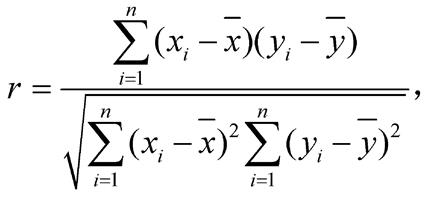
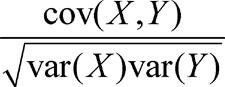
出处:管理学卷 • 统 计 学 • 概率论
相关系数 用以反映变量之间相关关系密切程度的统计指标。由英国统计学家皮尔逊(Karl Pearson,1857—1936)设计。根据研究对象的不同,分为:线性相关系数,反映两变量间线性相关关系的统计指标;非线性相关系数,反映两变量间曲线相关关系的统计指标;复相关系数,反映多元线性相关关系的统计指标。
出处:经济卷 • 统计学 • 统计学理论和方法 • 相关分析
相关系数(correlation coefficient) 统计分析中度量不同变量间关联程度和方向的统计指标。用r表示。相关系数的取值范围一般为(-1,+1)。相关系数的绝对值越接近于1,表示两个变量之间联系程度越大。相关系数小于0时,称为负相关;大于0时,称为正相关;等于0时,称为零相关。依据相关现象之间的不同特征,统计指标的名称亦有所不同。如将反映两变量间线性相关关系的统计指标称为相关系数(相关系数的平方称为决定系数或判定系数);反映两变量间曲线相关关系的统计指标称为非线性相关系数;将反映多元线性相关关系的统计指标称为复相关系数等。
出处:心理卷 • 心理统计与测量 • 心理统计 • 描述统计