词条	方差
释义	方差 天文学地球科学卷 方差 　　　　描述随机变量分布离散程度的一个数字特征。是随机变量X的取值(中心化)Δ1=x1-E(X),Δ2=x2-E(X),…,Δn=xn-E(X)的平方与其概率P1,P2,…,Pn的乘积和$\stackrel{n}{\underset{i=1}{\mathrm{\Sigma }}}$Pi${\Delta }_i^2$。符号以σ2表示。在测绘学的测量数据处理中,对一组观测误差Δ1,Δ2,…,Δn,可用方差σ2来度量误差离散程度,并作为精度指标。 出处：天文学地球科学卷 • 测　绘　学 • 大地测量学 • 测量平差 教育卷 方差（variance）　　差异量数的一种。随机变量ξ与其数学期望Eξ的偏差平方的加权平均E（ξ－Eξ）2。用Dξ或varξ表示。在概率论和数理统计中，表示随机变量和其数学期望（即均值）之间的偏离程度，即数据和中心偏离的程度。用来衡量一批数据的波动大小（即这批数据偏离平均数的大小）。在样本容量相同的情况下，方差越大，说明数据的波动越大，越不稳定。 出处：教育卷 • 教育原理 • 教育统计学 哲学卷 方差 　　概率论的基本概念。是随机变量ξ与其数学期望Eξ的偏差平方的加权平均E(ξ-Eξ)2。常记为Dξ或var ξ。随机变量的方差由其概率分布唯一确定,故亦称某分布的方差。它表示随机变量取值的分散程度。方差愈大,该随机变量的取值愈分散。方差愈小,该随机变量取值愈集中。方差的量纲是相应随机变量的量纲的平方,为了使量纲一致,实际中常用方差的平方根 　　,称为随机变量ξ的“根方差”“均方差”或“标准差”。对测量而言,总希望被测定的量愈接近其真值愈好,也就是使相应的方差尽可能地小。方差的平方根σ称为“中误差”。$\sqrt{D\xi }$ 出处：哲学卷 • 逻　辑　学 • 现代形式逻辑 政治学社会学卷 方差　　亦称“变异数”。某一变量的各个变量值与其平均数的离差平方和的平均数。其计算公式分别是:在未分组资料中, 　　　　 s2= 　　　　式中,s2为方差,x为各个变量值, 　　为各个变量值的算术平均数,n为变量值的个数。在已分组资料中,　　 s2=　　式中,f为分配到各组的变量值的次数,∑f为各组变量值的次数的总和,其他符号与上式中的相同。在社会统计中,方差是测量社会统计变量离散度或标志变动度的最佳指标之一。如果计算出的方差数值越大,则表示变量值分布的离散度也越大,反之则越小。$\frac{\text{∑}\text{(}x\text{-}\overline{x}{\text{)}}^2}{n}$$\overline{x}$$\frac{\text{∑}\text{(}x\text{-}\overline{x}{\text{)}}^{2}f}{\text{∑}f}$ 出处：政治学社会学卷 • 社　会　学 • 社会学方法 • 概念　术语 数理化力学卷 方差 　　　　随机变量ξ与其数学期望Eξ的偏差平方的加权平均E(ξ-Eξ)2。常记为Dξ或varξ。随机变量的方差由其概率分布唯一确定,故亦称某分布的方差。它表示随机变量取值的分散程度。方差愈大,该随机变量的取值愈分散。方差愈小,该随机变量取值愈集中。方差的量纲是相应随机变量的量纲的平方,为了使量纲一致,实际中常用方差的平方根,称为随机变量ξ的“根方差”、“均方差”或“标准差”。对测量而言,总希望被测定的量愈接近其真值愈好,也就是使相应的方差尽可能地小。 出处：数理化力学卷 • 数　　学 • 概率论 • 数理统计 管理学卷 方差　　设随机变量X的数学期望为EX,若E(X-EX)2存在,则称它为X的方差,记为var(X)或者DX。它是反映随机变量对于均值的偏离程度的数字特征。 出处：管理学卷 • 统　计　学 • 概率论 经济卷 方差 　　概率论的基本概念。随机变量（ζ）与其数学期望（Eζ）的偏差平方的加权平均（E（ζ－Eζ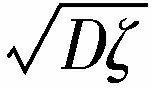）2）。常记为Dζ或varζ。随机变量的方差由概率分布唯一确定，故又称某分布的方差。它表示随机变量取值的分散程度。方差愈大，该随机变量的取值愈分散；方差愈小，该随机变量的取值愈集中。方差的量纲是相应随机变量的量纲的平方，为了使量纲一致，实际中常用方差的平方根，称为随机变量ζ的“根方差”、“均方差”或“标准差”。对测量而言，总希望被测定的量越接近其真值越好，也就是使相应的方差尽可能小。 出处：经济卷 • 统计学 • 统计学理论和方法 • 统计指标 心理卷 方差（variance）　　差异量数的一种。随机变量ξ与其数学期望Eξ的偏差平方的加权平均E（ξ－Eξ）2。用Dξ或varξ表示。在概率论和数理统计中，表示随机变量和其数学期望（即均值）之间的偏离程度，即数据和中心偏离的程度。用来衡量一批数据的波动大小（即这批数据偏离平均数的大小）。在样本容量相同的情况下，方差越大，说明数据的波动越大，越不稳定。 出处：心理卷 • 心理统计与测量 • 心理统计 • 描述统计
随便看	豞 豠 哈得孙河 哈得孙河画派 哈得孙海峡 哈得孙湾 哈得孙湾公司 哈得斯 哈得来环流 哈德成 哈德良 哈德良别墅 哈德良回忆录 哈德良离宫 哈德良长墙 哈恩 哈恰图良 哈扎拉人 哈托尔 哈拉 哈拉卓尔噶 哈拉卡 哈拉和卓 哈拉和林 哈拉姆

百科全书收录258893条中英文百科知识，基本涵盖了大多数领域的百科知识，是一部内容开放、自由的电子版百科全书。