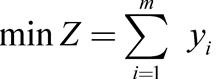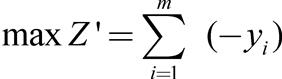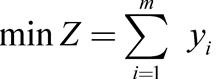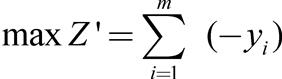词条	两阶段法
释义	两阶段法 管理学卷 两阶段法　　寻找线性规划问题初始基可行解的方法。把增加人工变量的线性规划问题分为两个阶段去求解。第一阶段是构造一个辅助的人工目标函数,即 　　或　　若原问题有可行解,则在本阶段的最终单纯形表中,必有Z=0和y i=0(1,2,…,m),并使人工变量均为非基变量。此时,划去人工变量所在的列与人工目标函数所在的行,就得到原问题的初始可行基对应的单纯形表,进入第二阶段。否则,在第一阶段的某张表中必有Z≠0,且人工变量中至少还有一个不为0的基变量。此时表明原问题无可行解,从而不必进行第二阶段,计算终止。第二阶段是在第一阶段得到的初始可行基对应的单纯形表的基础上,按原问题的目标函数进行换基迭代,直至求得原问题的最优解或判定无有限最优解。有时在第一阶段的最终表中,有可能出现Z=0,且在基变量中仍然含有一个或几个取值为0的人工变量(退化解)的情况。虽然现行基不可作为原问题的初始可行基,但此时,可继续进行一次或几次换基迭代,将基变量中的人工变量逐步替换为非基变量,而让不是人工变量的非基变量成为基变量。直至所有的人工变量均为非基变量时,才得到原问题的初始基本可行解,从而转入第二阶段。在大规模线性规划问题的求解中,通常采用两阶段法运算。。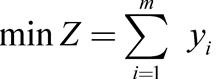 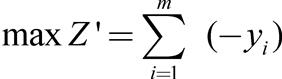出处：管理学卷 • 运　筹　学 • 数学规划
随便看	法伦理学 法伦理精神 法位学 法俄尔群岛 法俗 法偿货币 法像 法兰克人 法兰克尼亚王朝 法兰克王国 法兰克福书展 法兰克福和约 法兰克福国民议会 法兰克福学派 法兰克福学派美学 法兰克福宪法 法兰克福机场 法兰克福汇报 法兰克福证券交易所 法兰克福评论报 法兰士约瑟夫地群岛 法兰绒 法兰西人 法兰西人民联盟 法兰西共同体

百科全书收录258893条中英文百科知识，基本涵盖了大多数领域的百科知识，是一部内容开放、自由的电子版百科全书。