出处:数理化力学卷 • 数 学 • 运筹学 • 组合数学
多目标规划
多目标规划 规划论的一个分支。若规划问题中的衡量指标即目标函数不是一个,而是若干个,那么该问题就是多目标规划问题。如企业生产中往往要求取得较多的利润和总产值,同时又要损耗较少;如何安排生产,就是一种多目标规划问题。多目标规划与经济学、决策分析、系统理论等有密切的联系。
多目标规划 研究多于一个的实值目标函数(向量目标函数)在给定约束条件下的极值(极大化或极小化)问题的数学规划。有限维极小化形式的多目标规划问题(VMP)表示为:
。 其中X⊂Rn 是约束集,f:X➝R m 是(m维)向量目标函数,V-min表示“向量极小化”。设VMP中的约束集由不等式约束和等式约束表示为
X= 则VMP也记为 , 若f
, 若f k (x)(k=1,2,…,m)、g i (x)(i=1,2,…,p)和h j (x)(j=1,2,…,q)都是x的线性函数,则相应的问题称为多目标线性规划。若VMP的f k (x)(k=1,2,…,m)、g i (x)(i=1,2,…,p)和h j (x)(j=1,2,…,q)中有x的非线性函数,则称其为多目标非线性规划。在多目标规划的研究中,变量空间和目标空间均可不限于有限维的情况。对于这些空间是巴拿赫空间和拓扑向量空间的情形,已建有系统的数学理论。19世纪末20世纪初,埃奇沃思(Francis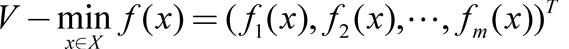
。 其中X⊂R
X= 则VMP也记为

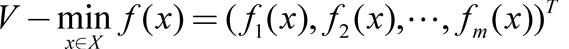
出处:管理学卷 • 运 筹 学 • 数学规划