词条	二项分布
释义	二项分布 教育卷 二项分布（binomial distribution）　　亦称“伯努利分布”。离散分布的一种。仅有两种不同性质结果的概率分布。因与二项式展开式相同而得名。由瑞士数学家伯努利（Daniel Bernoulli，1700—1782）创始。设有n次实验，各次实验彼此独立，每次实验某事件出现的概率都是p，不出现的概率q＝1－p，则对于某事件出现X次（0，1，2，…，n）的概率分布为P（x＝X）＝CXnpXqn－X。 出处：教育卷 • 教育原理 • 教育统计学 哲学卷 二项分布　　概率论的基本概念。描述随机现象的一种常用分布。例如,在抽查大批产品时,如果每次抽查结果出现次品的概率为p,则连续抽查n次,发现有k个次品的概率是: 　　因为对不同的k,它们正好是二项式[p+(1-p)] n的展开式的各个项,所以这种概率分布称为“二项分布”。一般地,只要每次试验结果发生某事件的概率为p,则独立地将此试验重复n次时,这个事件正好发生k次的概率就是P n(k)。 出处：哲学卷 • 逻　辑　学 • 现代形式逻辑 政治学社会学卷 二项分布　　描述随机现象的一种常用分布。例如,在抽查大批产品时,如果每次抽查结果出现次品的概率为p,则连续抽查n次,发现有k个次品的概率是: 　　　　 pn(k)=　　因为对不同的k,它们正好是二项式[p+(1-p)] n的展开式的各个项,所以这种概率分布称为“二项分布”。一般地,只要每次试验结果发生某事件的概率为p,则独立地将此试验重复n次时,这个事件正好发生k次的概率就是p n(k)。在社会统计中,二项分布专门用来描述每次抽样观测只有“男”或“女”、“是”或“不是”、“有”或“没有”、“知道”或“不知道”等两种可能状况的概率分布。 　　·pk(1-p)n-k(k=0,1,…,n)$\frac{n\text{(}n\text{-}1\text{)}\text{…}\text{(}n\text{-}k+1\text{)}}{k\text{(}k\text{-}1\text{)}\text{…}1}$ 出处：政治学社会学卷 • 社　会　学 • 社会学方法 • 概念　术语 数理化力学卷 二项分布　　描述随机现象的一种常用分布。例如,在抽查大批产品时,如果每次抽查结果出现次品的概率为p,则连续抽查n次,发现有k个次品的概率是: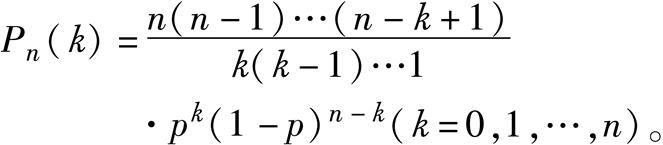 　　因为对不同的k,它们正好是二项式[p+(1-p)] n的展开式的各个项,所以这种概率分布称为“二项分布”。一般地,只要每次试验结果发生某事件的概率为p,则将此试验独立地重复n次时,这个事件正好发生k次的概率就是P n(k)。 出处：数理化力学卷 • 数　　学 • 概率论 • 数理统计 管理学卷 二项分布　　在n次重复独立的伯努利试验中,若以X记事件A出现的次数,则X的可能取值为0,1…,n,X的概率分布为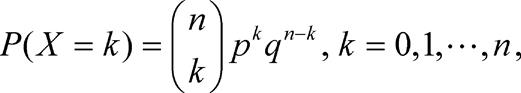 　　其中p为在一次试验中事件A出现的概率,q=1-p,称X服从二项分布,记为X~B(n,p)。 出处：管理学卷 • 统　计　学 • 概率论 心理卷 二项分布（binomial distribution）　　亦称“贝努里分布”。离散分布的一种。仅有两种不同性质结果的概率分布。因与二项式展开式相同而得名。由瑞士数学家贝努里创始。设有n次实验，各次实验彼此独立，每次实验某事件出现的概率都是p，不出现的概率q＝1－p，则对于某事件出现X次（0，1，2，…，n）的概率分布为P（x＝X）＝C XnpXqn－X。 出处：心理卷 • 心理统计与测量 • 心理统计 • 推论统计
随便看	谢贵 谢赫 谢赫学派 谢迁 谢过 谢通门 谢逸 谢道韫 谢里丹 谢里夫 谢里姆一世 谢里姆三世 谢里曼 谢金吾 谢雪红 谢霖 谢非 谢韦里亚宁 谢马克斯 谣 谣传 谣俗 谣曲 谣言 谣诼

百科全书收录258893条中英文百科知识，基本涵盖了大多数领域的百科知识，是一部内容开放、自由的电子版百科全书。