Bessel function
mathematics
also called Cylinder Function,
any of a set of mathematical functions systematically derived around 1817 by the German astronomer Friedrich Wilhelm Bessel during an investigation of solutions of one of Kepler's equations of planetary motion. Particular functions of the set had been formulated earlier by the Swiss mathematicians Daniel Bernoulli, who studied the oscillations of a chain suspended by one end, and Leonhard Euler, who analyzed the vibrations of a stretched membrane.
After Bessel published his findings, other scientists found that the functions appeared in mathematical descriptions of many physical phenomena, including the flow of heat or electricity in a solid cylinder, the propagation of electromagnetic waves along wires, the diffraction of light, the motions of fluids, and the deformations of elastic bodies. One of these investigators, Lord Rayleigh, also placed the Bessel functions in a larger context by showing that they arise in the solution of Laplace's equation (q.v.) when the latter is formulated in cylindrical (rather than Cartesian or spherical) coordinates.
Specifically, a Bessel function is a solution of the differential equation
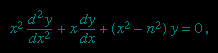
which is called Bessel's equation. For integral values of n, the Bessel functions are
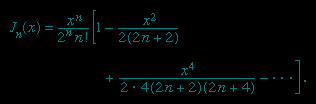
 The graph of J0(x) looks like that of a damped cosine curve, and that of J1(x) looks like that of a damped sine curve (see Graph-->
The graph of J0(x) looks like that of a damped cosine curve, and that of J1(x) looks like that of a damped sine curve (see Graph--> ).
).Certain physical problems lead to differential equations analogous to Bessel's equation; their solutions take the form of combinations of Bessel functions and are called Bessel functions of the second or third kind.
- Wilhelm von Giesebrecht
- Wilhelm von Grumbach
- Wilhelm von Kaulbach
- Wilhelm Wien
- Wilhelm Wundt
- Wilkes-Barre
- Wilkes, Charles
- Wilkes, John
- Wilkes Land
- Wilkie Collins
- Wilkie, Sir David
- Wilkins, Mac
- Wilkins, Maurice
- Wilkinson, James
- Wilkinson, Jemima
- Wilkinson, John
- Wilkinson Microwave Anisotropy Probe (WMAP)
- Wilkinson, Sir Geoffrey
- Wilkins, Roy
- Wilkins, Sir George Hubert
- will
- Willa Cather
- Willading, Johann Friedrich
- Willaert, Adriaan
- Willam Christensen