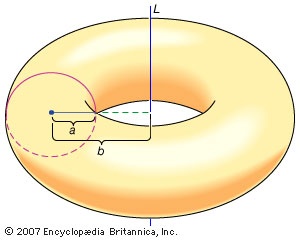in mathematics, theorem named for the 4th-century Greek geometer Pappus of Alexandria that describes the volume of a solid, obtained by revolving a plane region D about a line L not intersecting D, as the product of the area of D and the length of the circular path traversed by the centroid of D during the revolution. To illustrate--> Pappus's theorem, consider a circular disk of radius a units situated in a plane, and suppose that its centre is located b units from a line L in the same plane, measured perpendicularly, where b\\>a. When the disk is revolved through 360 degrees about L, its centre travels along a circular path of circumference 2πb units (twice the product of π and the radius of the path). Since the area of the disk is πa² square units (the product of π and the square of the radius of the disk), Pappus's theorem declares that the volume of the solid torus obtained is (πa²)×(2πb)=2π²a²b cubic units.