fluid mechanics
physics
Introduction
science concerned with the response of fluids to forces exerted upon them. It is a branch of classical physics with applications of great importance in hydraulic and aeronautical engineering, chemical engineering, meteorology, and zoology.
The most familiar fluid is of course water, and an encyclopaedia of the 19th century probably would have dealt with the subject under the separate headings of hydrostatics, the science of water at rest, and hydrodynamics, the science of water in motion. Archimedes founded hydrostatics in about 250 BC when, according to legend, he leapt out of his bath and ran naked through the streets of Syracuse crying “Eureka!”; it has undergone rather little development since. The foundations of hydrodynamics, on the other hand, were not laid until the 18th century when mathematicians such as Leonhard Euler and Daniel Bernoulli began to explore the consequences, for a virtually continuous medium like water, of the dynamic principles that Newton had enunciated for systems composed of discrete particles. Their work was continued in the 19th century by several mathematicians and physicists of the first rank, notably G.G. Stokes and William Thomson. By the end of the century explanations had been found for a host of intriguing phenomena having to do with the flow of water through tubes and orifices, the waves that ships moving through water leave behind them, raindrops on windowpanes, and the like. There was still no proper understanding, however, of problems as fundamental as that of water flowing past a fixed obstacle and exerting a drag force upon it; the theory of potential flow, which worked so well in other contexts, yielded results that at relatively high flow rates were grossly at variance with experiment. This problem was not properly understood until 1904, when the German physicist Ludwig Prandtl (Prandtl, Ludwig) introduced the concept of the boundary layer (see below Hydrodynamics: Boundary layers and separation (fluid mechanics)). Prandtl's career continued into the period in which the first manned aircraft were developed. Since that time, the flow of air (aerodynamics) has been of as much interest to physicists and engineers as the flow of water, and hydrodynamics has, as a consequence, become fluid dynamics. The term fluid mechanics, as used here, embraces both fluid dynamics and the subject still generally referred to as hydrostatics.
One other representative of the 20th century who deserves mention here besides Prandtl is Geoffrey Taylor of England. Taylor remained a classical physicist while most of his contemporaries were turning their attention to the problems of atomic structure and quantum mechanics, and he made several unexpected and important discoveries in the field of fluid mechanics. The richness of fluid mechanics is due in large part to a term in the basic equation of the motion of fluids which is nonlinear—i.e., one that involves the fluid velocity twice over. It is characteristic of systems described by nonlinear equations that under certain conditions they become unstable and begin behaving in ways that seem at first sight to be totally chaotic. In the case of fluids, chaotic behaviour is very common and is called turbulence. Mathematicians have now begun to recognize patterns in chaos (chaos theory) that can be analyzed fruitfully, and this development suggests that fluid mechanics will remain a field of active research well into the 21st century. (For a discussion of the concept of chaos, see physical science, principles of.)
Fluid mechanics is a subject with almost endless ramifications, and the account that follows is necessarily incomplete. Some knowledge of the basic properties of fluids will be needed; a survey of the most relevant properties is given in the next section. For further details, see thermodynamics and liquid.
Basic properties of fluids (fluid)
Fluids are not strictly continuous media in the way that all the successors of Euler and Bernoulli have assumed, for they are composed of discrete molecules. The molecules, however, are so small and, except in gases at very low pressures, the number of molecules per millilitre is so enormous that they need not be viewed as individual entities. There are a few liquids, known as liquid crystals, in which the molecules are packed together in such a way as to make the properties of the medium locally anisotropic (anisotropy), but the vast majority of fluids (including air and water) are isotropic. In fluid mechanics, the state of an isotropic fluid may be completely described by defining its mean mass per unit volume, or density (ρ), its temperature (T), and its velocity (v) at every point in space, and just what the connection is between these macroscopic properties and the positions and velocities of individual molecules is of no direct relevance.
A word perhaps is needed about the difference between gases (gas) and liquids (liquid), though the difference is easier to perceive than to describe. In gases the molecules are sufficiently far apart to move almost independently of one another, and gases tend to expand to fill any volume available to them. In liquids the molecules are more or less in contact, and the short-range attractive forces between them make them cohere; the molecules are moving too fast to settle down into the ordered arrays that are characteristic of solids, but not so fast that they can fly apart. Thus, samples of liquid can exist as drops or as jets with free surfaces, or they can sit in beakers constrained only by gravity, in a way that samples of gas cannot. Such samples may evaporate in time, as molecules one by one pick up enough speed to escape across the free surface and are not replaced. The lifetime of liquid drops and jets, however, is normally long enough for evaporation to be ignored.
There are two sorts of stress that may exist in any solid or fluid medium, and the difference between them may be illustrated by reference to a brick held between two hands. If the holder moves his hands toward each other, he exerts pressure on the brick; if he moves one hand toward his body and the other away from it, then he exerts what is called a shear stress. A solid substance such as a brick can withstand stresses of both types, but fluids, by definition, yield to shear stresses no matter how small these stresses may be. They do so at a rate determined by the fluid's viscosity. This property, about which more will be said later, is a measure of the friction that arises when adjacent layers of fluid slip over one another. It follows that the shear stresses are everywhere zero in a fluid at rest and in equilibrium, and from this it follows that the pressure (that is, force per unit area) acting perpendicular to all planes in the fluid is the same irrespective of their orientation (Pascal's law (Pascal's principle)). For an isotropic fluid in equilibrium there is only one value of the local pressure (p) consistent with the stated values for ρ and T. These three quantities are linked together by what is called the equation of state (state, equation of) for the fluid.
For gases at low pressures the equation of state is simple and well known. It is
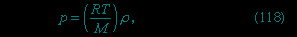
where R is the universal gas constant (8.3 joules per degree Celsius per mole) and M is the molar mass, or an average molar mass if the gas is a mixture; for air, the appropriate average is about 29 × 10−3 kilogram per mole. For other fluids knowledge of the equation of state is often incomplete. Except under very extreme conditions, however, all one needs to know is how the density changes when the pressure is changed by a small amount, and this is described by the compressibility of the fluid—either the isothermal compressibility, βT, or the adiabatic compressibility, βS, according to circumstance. When an element of fluid is compressed, the work done on it tends to heat it up. If the heat has time to drain away to the surroundings and the temperature of the fluid remains essentially unchanged throughout, then βT is the relevant quantity. If virtually none of the heat escapes, as is more commonly the case in flow problems because the thermal conductivity of most fluids is poor, then the flow is said to be adiabatic, and βS is needed instead. (The S refers to entropy, which remains constant in an adiabatic process provided that it takes place slowly enough to be treated as “reversible” in the thermodynamic sense.) For gases that obey equation (118-->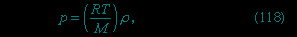 ), it is evident that p and ρ are proportional to one another in an isothermal process, and
), it is evident that p and ρ are proportional to one another in an isothermal process, and
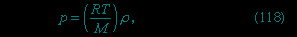 ), it is evident that p and ρ are proportional to one another in an isothermal process, and
), it is evident that p and ρ are proportional to one another in an isothermal process, and
In reversible adiabatic processes for such gases, however, the temperature rises on compression at a rate such that
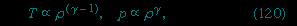
and
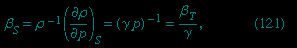
where γ is about 1.4 for air and takes similar values for other common gases. For liquids the ratio between the isothermal and adiabatic compressibilities is much closer to unity. For liquids, however, both compressibilities are normally much less than p−1, and the simplifying assumption that they are zero is often justified.
The factor γ is not only the ratio between two compressibilities; it is also the ratio between two principal specific heats (specific heat). The molar specific heat is the amount of heat required to raise the temperature of one mole through one degree. This is greater if the substance is allowed to expand as it is heated, and therefore to do work, than if its volume is fixed. The principal molar specific heats, CP and CV, refer to heating at constant pressure and constant volume, respectively, and

For air, CP is about 3.5 R.
Solids can be stretched without breaking, and liquids, though not gases, can withstand stretching, too. Thus, if the pressure is steadily reduced in a specimen of very pure water, bubbles will ultimately appear, but they may not do so until the pressure is negative and well below -107 newton per square metre; this is 100 times greater in magnitude than the (positive) pressure exerted by the Earth's atmosphere. Water owes its high ideal strength to the fact that rupture involves breaking links of attraction between molecules on either side of the plane on which rupture occurs; work must be done to break these links. However, its strength is drastically reduced by anything that provides a nucleus at which the process known as cavitation (formation of vapour- or gas-filled cavities) can begin, and a liquid containing suspended dust particles or dissolved gases is liable to cavitate quite easily.
Work also must be done if a free liquid drop of spherical shape is to be drawn out into a long thin cylinder or deformed in any other way that increases its surface area. Here again work is needed to break intermolecular links. The surface of a liquid behaves, in fact, as if it were an elastic membrane under tension, except that the tension exerted by an elastic membrane increases when the membrane is stretched in a way that the tension exerted by a liquid surface does not. surface tension is what causes liquids to rise up capillary tubes, what supports hanging liquid drops, what limits the formation of ripples on the surface of liquids, and so on.
Hydrostatics
It is common knowledge that the pressure of the atmosphere (about 105 newtons per square metre) is due to the weight of air above the Earth's surface, that this pressure falls as one climbs upward, and, correspondingly, that pressure increases as one dives deeper into a lake (or comparable body of water). Mathematically, the rate at which the pressure in a stationary fluid varies with height z in a vertical gravitational field of strength g is given by

If ρ and g are both independent of z, as is more or less the case in lakes, then
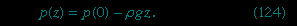
This means that, since ρ is about 103 kilograms per cubic metre for water and g is about 10 metres per second squared, the pressure is already twice the atmospheric value at a depth of 10 metres. Applied to the atmosphere, equation (124-->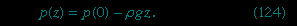 ) would imply that the pressure falls to zero at a height of about 10 kilometres. In the atmosphere, however, the variation of ρ with z is far from negligible and (124-->
) would imply that the pressure falls to zero at a height of about 10 kilometres. In the atmosphere, however, the variation of ρ with z is far from negligible and (124-->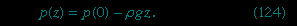 ) is unreliable as a consequence; a better approximation is given below in the section Hydrodynamics: Compressible flow in gases (fluid mechanics).
) is unreliable as a consequence; a better approximation is given below in the section Hydrodynamics: Compressible flow in gases (fluid mechanics).
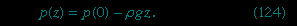 ) would imply that the pressure falls to zero at a height of about 10 kilometres. In the atmosphere, however, the variation of ρ with z is far from negligible and (124-->
) would imply that the pressure falls to zero at a height of about 10 kilometres. In the atmosphere, however, the variation of ρ with z is far from negligible and (124-->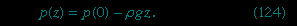 ) is unreliable as a consequence; a better approximation is given below in the section Hydrodynamics: Compressible flow in gases (fluid mechanics).
) is unreliable as a consequence; a better approximation is given below in the section Hydrodynamics: Compressible flow in gases (fluid mechanics).Differential manometers
 Special Comp-->
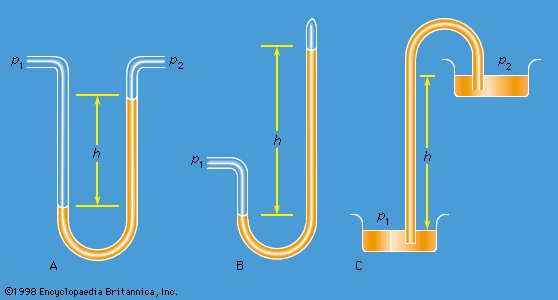
Special Comp-->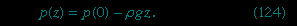 Instruments for comparing pressures are called differential manometers, and the simplest such instrument is a U-tube containing liquid, as shown in Figure 1A-->
Instruments for comparing pressures are called differential manometers, and the simplest such instrument is a U-tube containing liquid, as shown in Figure 1A--> . The two pressures of interest, p1 and p2, are transmitted to the two ends of the liquid column through an inert gas—the density of which is negligible by comparison with the liquid density, ρ—and the difference of height, h, of the two menisci is measured. It is a consequence of (124-->
. The two pressures of interest, p1 and p2, are transmitted to the two ends of the liquid column through an inert gas—the density of which is negligible by comparison with the liquid density, ρ—and the difference of height, h, of the two menisci is measured. It is a consequence of (124-->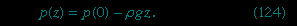 ) that
) that
 A barometer for measuring the pressure of the atmosphere in absolute terms is simply a manometer in which p2 is made zero, or as close to zero as is feasible. The barometer invented in the 17th century by the Italian physicist and mathematician Evangelista Torricelli (Torricelli, Evangelista), and still in use today, is a U-tube that is sealed at one end (see Figure 1B-->
A barometer for measuring the pressure of the atmosphere in absolute terms is simply a manometer in which p2 is made zero, or as close to zero as is feasible. The barometer invented in the 17th century by the Italian physicist and mathematician Evangelista Torricelli (Torricelli, Evangelista), and still in use today, is a U-tube that is sealed at one end (see Figure 1B--> ). It may be filled with liquid, with the sealed end downward, and then inverted. On inversion, a negative pressure may momentarily develop at the top of the liquid column if the column is long enough; however, cavitation normally occurs there and the column falls away from the sealed end of the tube, as shown in the figure. Between the two exists what Torricelli thought of as a vacuum, though it may be very far from that condition if the barometer has been filled without scrupulous precautions to ensure that all dissolved or adsorbed gases, which would otherwise collect in this space, have first been removed. Even if no contaminating gas is present, the Torricellian vacuum always contains the vapour of the liquid, and this exerts a pressure which may be small but is never quite zero. The liquid conventionally used in a Torricelli barometer is of course mercury, which has a low vapour pressure and a high density. The high density means that h is only about 760 millimetres; if water were used, it would have to be about 10 metres instead.
). It may be filled with liquid, with the sealed end downward, and then inverted. On inversion, a negative pressure may momentarily develop at the top of the liquid column if the column is long enough; however, cavitation normally occurs there and the column falls away from the sealed end of the tube, as shown in the figure. Between the two exists what Torricelli thought of as a vacuum, though it may be very far from that condition if the barometer has been filled without scrupulous precautions to ensure that all dissolved or adsorbed gases, which would otherwise collect in this space, have first been removed. Even if no contaminating gas is present, the Torricellian vacuum always contains the vapour of the liquid, and this exerts a pressure which may be small but is never quite zero. The liquid conventionally used in a Torricelli barometer is of course mercury, which has a low vapour pressure and a high density. The high density means that h is only about 760 millimetres; if water were used, it would have to be about 10 metres instead. Figure 1C-->
Figure 1C--> illustrates the principle of the siphon. The top container is open to the atmosphere, and the pressure in it, p2, is therefore atmospheric. To balance this and the weight of the liquid column in between, the pressure p1 in the bottom container ought to be greater by ρgh. If the bottom container is also open to the atmosphere, then equilibrium is clearly impossible; the weight of the liquid column prevails and causes the liquid to flow downward. The siphon operates only as long as the column is continuous; it fails if a bubble of gas collects in the tube or if cavitation occurs. Cavitation therefore limits the level differences over which siphons can be used, and it also limits (to about 10 metres) the depth of wells from which water can be pumped using suction alone.
illustrates the principle of the siphon. The top container is open to the atmosphere, and the pressure in it, p2, is therefore atmospheric. To balance this and the weight of the liquid column in between, the pressure p1 in the bottom container ought to be greater by ρgh. If the bottom container is also open to the atmosphere, then equilibrium is clearly impossible; the weight of the liquid column prevails and causes the liquid to flow downward. The siphon operates only as long as the column is continuous; it fails if a bubble of gas collects in the tube or if cavitation occurs. Cavitation therefore limits the level differences over which siphons can be used, and it also limits (to about 10 metres) the depth of wells from which water can be pumped using suction alone. Archimedes' principle
Consider now a cube of side d totally immersed in liquid with its top and bottom faces horizontal. The pressure on the bottom face will be higher than on the top by ρgd, and, since pressure is force per unit area and the area of a cube face is d2, the resultant upthrust on the cube is ρgd3. This is a simple example of the so-called Archimedes' principle, which states that the upthrust experienced by a submerged or floating body is always equal to the weight of the liquid that the body displaces. As Archimedes must have realized, there is no need to prove this by detailed examination of the pressure difference between top and bottom. It is obviously true, whatever the body's shape. It is obvious because, if the solid body could somehow be removed and if the cavity thereby created could somehow be filled with more fluid instead, the whole system would still be in equilibrium. The extra fluid would, however, then be experiencing the upthrust previously experienced by the solid body, and it would not be in equilibrium unless this were just sufficient to balance its weight.
Archimedes' problem was to discover, by what would nowadays be called a nondestructive test, whether the crown of King Hieron II was made of pure gold or of gold diluted with silver. He understood that the pure metal and the alloy would differ in density and that he could determine the density of the crown by weighing it to find its mass and making a separate measurement of its volume. Perhaps the inspiration that struck him (in his bath) was that one can find the volume of any object by submerging it in liquid in something like a measuring cylinder (i.e., in a container with vertical sides that have been suitably graduated) and measuring the displacement of the liquid surface. If so, he no doubt realized soon afterward that a more elegant and more accurate method for determining density can be based on the principle that bears his name. This method involves weighing the object twice, first, when it is suspended in a vacuum (suspension in air will normally suffice) and, second, when it is totally submerged in a liquid of density ρ. If the density of the object is ρ′, the ratio between the two weights must be

If ρ′ is less than ρ, then W2, according to equation (126--> ), is negative. What that means is that the object does not submerge of its own accord; it has to be pushed downward to make it do so. If an object with a mean density less than that of water is placed in a lake and not subjected to any downward force other than its own weight, it naturally floats on the surface, and Archimedes' principle shows that in equilibrium the volume of water which it displaces is a fraction ρ′/ρ of its own volume. A hydrometer is an object graduated in such a way that this fraction may be measured. By floating a hydrometer first in water of density ρ0 and then in some other liquid of density ρ1 and comparing the readings, one may determine the ratio ρ1/ρ0—i.e., the specific gravity of the other liquid.
), is negative. What that means is that the object does not submerge of its own accord; it has to be pushed downward to make it do so. If an object with a mean density less than that of water is placed in a lake and not subjected to any downward force other than its own weight, it naturally floats on the surface, and Archimedes' principle shows that in equilibrium the volume of water which it displaces is a fraction ρ′/ρ of its own volume. A hydrometer is an object graduated in such a way that this fraction may be measured. By floating a hydrometer first in water of density ρ0 and then in some other liquid of density ρ1 and comparing the readings, one may determine the ratio ρ1/ρ0—i.e., the specific gravity of the other liquid.
 ), is negative. What that means is that the object does not submerge of its own accord; it has to be pushed downward to make it do so. If an object with a mean density less than that of water is placed in a lake and not subjected to any downward force other than its own weight, it naturally floats on the surface, and Archimedes' principle shows that in equilibrium the volume of water which it displaces is a fraction ρ′/ρ of its own volume. A hydrometer is an object graduated in such a way that this fraction may be measured. By floating a hydrometer first in water of density ρ0 and then in some other liquid of density ρ1 and comparing the readings, one may determine the ratio ρ1/ρ0—i.e., the specific gravity of the other liquid.
), is negative. What that means is that the object does not submerge of its own accord; it has to be pushed downward to make it do so. If an object with a mean density less than that of water is placed in a lake and not subjected to any downward force other than its own weight, it naturally floats on the surface, and Archimedes' principle shows that in equilibrium the volume of water which it displaces is a fraction ρ′/ρ of its own volume. A hydrometer is an object graduated in such a way that this fraction may be measured. By floating a hydrometer first in water of density ρ0 and then in some other liquid of density ρ1 and comparing the readings, one may determine the ratio ρ1/ρ0—i.e., the specific gravity of the other liquid.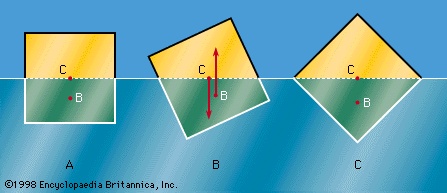






 In what orientation an object floats is a matter of grave concern to those who design boats and those who travel in them. A simple example will suffice to illustrate the factors that determine orientation. Figure 2-->
In what orientation an object floats is a matter of grave concern to those who design boats and those who travel in them. A simple example will suffice to illustrate the factors that determine orientation. Figure 2--> shows three of the many possible orientations that a uniform square prism might adopt when floating, with half its volume submerged in a liquid for which ρ = 2ρ′; they are separated by rotations of 22.5°. In each of these diagrams, C is the centre of mass of the prism, and B, a point known as the centre of buoyancy, is the centre of mass of the displaced water. The distributed forces acting on the prism are equivalent to its weight acting downward through C and to the equal weight of the displaced water acting upward through B. In general, therefore, the prism experiences a torque. In Figure 2B-->
shows three of the many possible orientations that a uniform square prism might adopt when floating, with half its volume submerged in a liquid for which ρ = 2ρ′; they are separated by rotations of 22.5°. In each of these diagrams, C is the centre of mass of the prism, and B, a point known as the centre of buoyancy, is the centre of mass of the displaced water. The distributed forces acting on the prism are equivalent to its weight acting downward through C and to the equal weight of the displaced water acting upward through B. In general, therefore, the prism experiences a torque. In Figure 2B--> the torque is counterclockwise, and so it turns the prism away from 2A-->
the torque is counterclockwise, and so it turns the prism away from 2A--> and toward 2C-->
and toward 2C--> . In 2C-->
. In 2C--> the torque vanishes because B is now vertically below C, and this is the orientation that corresponds to stable equilibrium. The torque also vanishes in 2A-->
the torque vanishes because B is now vertically below C, and this is the orientation that corresponds to stable equilibrium. The torque also vanishes in 2A--> , and the prism can in principle remain indefinitely in that orientation as well; the equilibrium in this case, however, is unstable, and the slightest disturbance will cause the prism to topple one way or the other. In fact, the potential energy of the system, which increases in a linear fashion with the difference in height between C and B, is at its smallest in orientation 2C-->
, and the prism can in principle remain indefinitely in that orientation as well; the equilibrium in this case, however, is unstable, and the slightest disturbance will cause the prism to topple one way or the other. In fact, the potential energy of the system, which increases in a linear fashion with the difference in height between C and B, is at its smallest in orientation 2C--> and at its largest in orientation 2A-->
and at its largest in orientation 2A--> . To improve the stability of a floating object one should, if possible, lower C relative to B. In the case of a boat, this may be done by redistributing the load inside.
. To improve the stability of a floating object one should, if possible, lower C relative to B. In the case of a boat, this may be done by redistributing the load inside.Surface tension of liquids
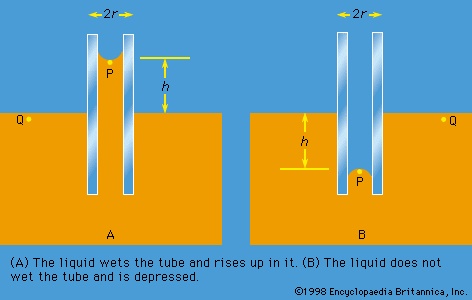
Of the many hydrostatic phenomena in which the surface tension of liquids plays a role, the most significant is probably capillarity. Consider what happens when a tube of narrow bore, often called a capillary tube, is dipped into a liquid. If the liquid “wets” the tube (with zero contact angle), the liquid surface inside the tube forms a concave meniscus, which is a virtually spherical surface having the same radius, r, as the inside of the tube. The tube experiences a downward force of magnitude 2πrdσ, where σ is the surface tension of the liquid, and the liquid experiences a reaction of equal magnitude that lifts the meniscus through a height h such that

 Special Comp-->
Special Comp--> —i.e., until the upward force for which surface tension is responsible is balanced by the weight of the column of liquid that has been lifted. If the liquid does not wet the tube, the meniscus is convex and depressed through the same distance h (see Figure 3-->
—i.e., until the upward force for which surface tension is responsible is balanced by the weight of the column of liquid that has been lifted. If the liquid does not wet the tube, the meniscus is convex and depressed through the same distance h (see Figure 3--> ). A simple method for determining surface tension involves the measurement of h in one or the other of these situations and the use of equation (127-->
). A simple method for determining surface tension involves the measurement of h in one or the other of these situations and the use of equation (127--> ) thereafter.
) thereafter.It follows from equations (124-->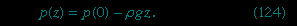 ) and (127-->
) and (127--> ) that the pressure at a point P just below the meniscus differs from the pressure at Q by an amount
) that the pressure at a point P just below the meniscus differs from the pressure at Q by an amount
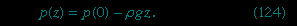 ) and (127-->
) and (127--> ) that the pressure at a point P just below the meniscus differs from the pressure at Q by an amount
) that the pressure at a point P just below the meniscus differs from the pressure at Q by an amount
 it is less than the pressure at Q in the case to which Figure 3A-->
it is less than the pressure at Q in the case to which Figure 3A--> refers and greater than the pressure at Q in the other case. Since the pressure at Q is just the atmospheric pressure, it is equal to the pressure at a point immediately above the meniscus. Hence, in both instances there is a pressure difference of 2σ/r between the two sides of the curved meniscus, and in both the higher pressure is on the inner side of the curve. Such a pressure difference is a requirement of equilibrium wherever a liquid surface is curved. If the surface is curved but not spherical, the pressure difference is
refers and greater than the pressure at Q in the other case. Since the pressure at Q is just the atmospheric pressure, it is equal to the pressure at a point immediately above the meniscus. Hence, in both instances there is a pressure difference of 2σ/r between the two sides of the curved meniscus, and in both the higher pressure is on the inner side of the curve. Such a pressure difference is a requirement of equilibrium wherever a liquid surface is curved. If the surface is curved but not spherical, the pressure difference is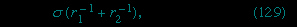
where r1 and r2 are the two principal radii of curvature. If it is cylindrical, one of these radii is infinite, and, if it is curved in opposite directions, then for the purposes of (129-->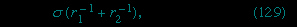 ) they should be treated as being of opposite sign.
) they should be treated as being of opposite sign.
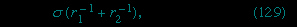 ) they should be treated as being of opposite sign.
) they should be treated as being of opposite sign. The diagrams in Figure 3-->
The diagrams in Figure 3--> were drawn to represent cross sections through cylindrical tubes, but they might equally well represent two vertical parallel plates that are partly submerged in the liquid a small distance apart. Consideration of how the pressure varies with height shows that over the range of height h the plates experience a greater pressure on their outer surfaces than on their inner surfaces; this is true whether the liquid wets both plates or not. It is a matter of observation that small objects floating near one another on the surface of a liquid tend to move toward one another, and it is the pressure difference just referred to that makes them behave in this way.
were drawn to represent cross sections through cylindrical tubes, but they might equally well represent two vertical parallel plates that are partly submerged in the liquid a small distance apart. Consideration of how the pressure varies with height shows that over the range of height h the plates experience a greater pressure on their outer surfaces than on their inner surfaces; this is true whether the liquid wets both plates or not. It is a matter of observation that small objects floating near one another on the surface of a liquid tend to move toward one another, and it is the pressure difference just referred to that makes them behave in this way. Special Comp-->
Special Comp-->

 One other problem having to do with surface tension will be considered here. The diagrams in Figure 4-->
One other problem having to do with surface tension will be considered here. The diagrams in Figure 4--> show stages in the growth of a liquid drop on the end of a tube which the liquid is supposed to wet. In passing from stage A to stage B, by which time the drop is roughly hemispheric in shape, the radius of curvature of the drop diminishes; and it follows from (128-->
show stages in the growth of a liquid drop on the end of a tube which the liquid is supposed to wet. In passing from stage A to stage B, by which time the drop is roughly hemispheric in shape, the radius of curvature of the drop diminishes; and it follows from (128--> ) that, to bring about this growth, one must slowly increase the pressure of the liquid inside the tube. If the pressure could be held steady at the value corresponding to B, the drop would then become unstable, because any further growth (e.g., to the more or less spherical shape indicated in Figure 4C-->
) that, to bring about this growth, one must slowly increase the pressure of the liquid inside the tube. If the pressure could be held steady at the value corresponding to B, the drop would then become unstable, because any further growth (e.g., to the more or less spherical shape indicated in Figure 4C--> ) would involve an increase in radius of curvature. The applied pressure would then exceed that required to hold the drop in equilibrium, and the drop would necessarily grow bigger still. In practice, however, it is easier to control the rate of flow of water through the tube, and hence the rate of growth of the drop, than it is to control the pressure. If the rate of flow is very small, drops will form the nonspherical shapes suggested by Figure 4D-->
) would involve an increase in radius of curvature. The applied pressure would then exceed that required to hold the drop in equilibrium, and the drop would necessarily grow bigger still. In practice, however, it is easier to control the rate of flow of water through the tube, and hence the rate of growth of the drop, than it is to control the pressure. If the rate of flow is very small, drops will form the nonspherical shapes suggested by Figure 4D--> before they detach themselves and fall. It is not an easy matter to analyze the shape of a drop on the point of detachment, and there is no simple formula for the volume of the drop after it is detached.
before they detach themselves and fall. It is not an easy matter to analyze the shape of a drop on the point of detachment, and there is no simple formula for the volume of the drop after it is detached.Hydrodynamics
Bernoulli's law (Bernoulli's theorem)
Up to now the focus has been fluids at rest. This section deals with fluids that are in motion in a steady fashion such that the fluid velocity at each given point in space is not changing with time. Any flow pattern that is steady in this sense may be seen in terms of a set of streamlines, the trajectories of imaginary particles suspended in the fluid and carried along with it. In steady flow, the fluid is in motion but the streamlines are fixed. Where the streamlines crowd together, the fluid velocity is relatively high; where they open out, the fluid becomes relatively stagnant.
When Euler (Euler, Leonhard) and Bernoulli (Bernoulli, Daniel) were laying the foundations of hydrodynamics, they treated the fluid as an idealized inviscid substance in which, as in a fluid at rest in equilibrium, the shear stresses associated with viscosity are zero and the pressure p is isotropic. They arrived at a simple law relating the variation of p along a streamline to the variation of v (the principle is credited to Bernoulli, but Euler seems to have arrived at it first), which serves to explain many of the phenomena that real fluids in steady motion display. To the inevitable question of when and why it is justifiable to neglect viscosity, there is no single answer. Some answers will be provided later in this article, but other matters will be taken up first.
Consider a small element of fluid of mass m, which—apart from the force on it due to gravity—is acted on only by a pressure p. The latter is isotropic and does not vary with time but may vary from point to point in space. It is a well-known consequence of Newton's laws of motion that, when a particle of mass m moves under the influence of its weight mg and an additional force F from a point P where its speed is vP and its height is zP to a point Q where its speed is vQ and its height is zQ, the work done by the additional force is equal to the increase in kinetic and potential energy of the particle—i.e., that
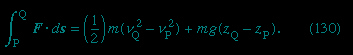
In the case of the fluid element under consideration, F may be related in a simple fashion to the gradient of the pressure, and one finds
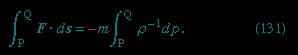
If the variations of fluid density along the streamline from P to Q are negligibly small, the factor ρ−1 may be taken outside the integral on the right-hand side of (131-->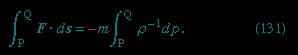 ), which thereupon reduces to ρ−1(pQ - pP). Then (130-->
), which thereupon reduces to ρ−1(pQ - pP). Then (130-->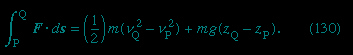 ) and (131-->
) and (131-->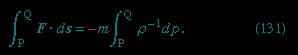 ) can be combined to obtain
) can be combined to obtain
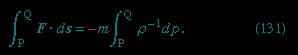 ), which thereupon reduces to ρ−1(pQ - pP). Then (130-->
), which thereupon reduces to ρ−1(pQ - pP). Then (130-->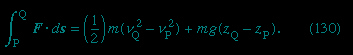 ) and (131-->
) and (131-->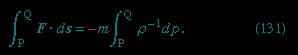 ) can be combined to obtain
) can be combined to obtain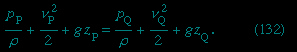
Since this applies for any two points that can be visited by a single element of fluid, one can immediately deduce Bernoulli's (or Euler's) important result that along each streamline in the steady flow of an inviscid fluid the quantity
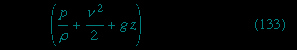
is constant.
Under what circumstances are variations in the density negligibly small? When they are very small compared with the density itself—i.e., when
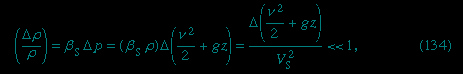
where the symbol Δ is used to represent the extent of the change along a streamline of the quantity that follows it, and where Vs is the speed of sound (see below Compressible flow in gases (fluid mechanics)). This condition is satisfied for all the flow problems having to do with water that are discussed below. If the fluid is air, it is adequately satisfied provided that the largest excursion in z is on the order of metres rather than kilometres and provided that the fluid velocity is everywhere less than about 100 metres per second.
Bernoulli's law indicates that, if an inviscid fluid is flowing along a pipe of varying cross section, then the pressure is relatively low at constrictions where the velocity is high and relatively high where the pipe opens out and the fluid stagnates. Many people find this situation paradoxical when they first encounter it. Surely, they say, a constriction should increase the local pressure rather than diminish it? The paradox evaporates as one learns to think of the pressure changes along the pipe as cause and the velocity changes as effect, instead of the other way around; it is only because the pressure falls at a constriction that the pressure gradient upstream of the constriction has the right sign to make the fluid accelerate.
Paradoxical or not, predictions based on Bernoulli's law are well-verified by experiment. Try holding two sheets of paper so that they hang vertically two centimetres or so apart and blow downward so that there is a current of air between them. The sheets will be drawn together by the reduction in pressure associated with this current. Ships are drawn together for much the same reason if they are moving through the water in the same direction at the same speed with a small distance between them. In this case, the current results from the displacement of water by each ship's bow, which has to flow backward to fill the space created as the stern moves forward, and the current between the ships, to which they both contribute, is stronger than the current moving past their outer sides. As another simple experiment, listen to the hissing sound made by a tap that is almost, but not quite, turned off. What happens in this case is that the flow is so constricted and the velocity within the constriction so high that the pressure in the constriction is actually negative. Assisted by the dissolved gases that are normally present, the water cavitates as it passes through, and the noise that is heard is the sound of tiny bubbles collapsing as the water slows down and the pressure rises again on the other side.
 Two practical devices that are used by hydraulic engineers to monitor the flow of liquids though pipes are based on Bernoulli's law. One is the venturi tube, a short length with a constriction in it of standard shape (see Figure 5A-->
Two practical devices that are used by hydraulic engineers to monitor the flow of liquids though pipes are based on Bernoulli's law. One is the venturi tube, a short length with a constriction in it of standard shape (see Figure 5A--> ), which may be inserted into the pipe proper. If the velocity at point P, where the tube has a cross-sectional area AP, is vP and the velocity in the constriction, where the area is AQ, is vQ, the continuity condition—the condition that the mass flowing through the pipe per unit time has to be the same at all points along its length—suggests that ρPAPvP = ρQAQvQ, or that APvP = AQvQ if the difference between ρP and ρQ is negligible. Then Bernoulli's law indicates
), which may be inserted into the pipe proper. If the velocity at point P, where the tube has a cross-sectional area AP, is vP and the velocity in the constriction, where the area is AQ, is vQ, the continuity condition—the condition that the mass flowing through the pipe per unit time has to be the same at all points along its length—suggests that ρPAPvP = ρQAQvQ, or that APvP = AQvQ if the difference between ρP and ρQ is negligible. Then Bernoulli's law indicates 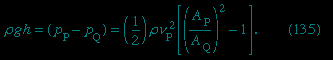
Thus one should be able to find vP, and hence the quantity Q (= APvP) that engineers refer to as the rate of discharge, by measuring the difference of level h of the fluid in the two side tubes shown in the diagram. At low velocities the pressure difference (pP - pQ) is greatly affected by viscosity (see below Viscosity (fluid mechanics)), and equation (135-->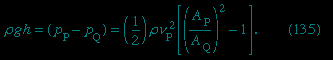 ) is unreliable in consequence. The venturi tube is normally used, however, when the velocity is large enough for the flow to be turbulent (see below Turbulence (fluid mechanics)). In such a circumstance, equation (135) predicts values for Q that agree with values measured by more direct means to within a few parts percent, even though the flow pattern is not really steady at all.
) is unreliable in consequence. The venturi tube is normally used, however, when the velocity is large enough for the flow to be turbulent (see below Turbulence (fluid mechanics)). In such a circumstance, equation (135) predicts values for Q that agree with values measured by more direct means to within a few parts percent, even though the flow pattern is not really steady at all.
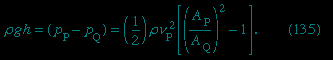 ) is unreliable in consequence. The venturi tube is normally used, however, when the velocity is large enough for the flow to be turbulent (see below Turbulence (fluid mechanics)). In such a circumstance, equation (135) predicts values for Q that agree with values measured by more direct means to within a few parts percent, even though the flow pattern is not really steady at all.
) is unreliable in consequence. The venturi tube is normally used, however, when the velocity is large enough for the flow to be turbulent (see below Turbulence (fluid mechanics)). In such a circumstance, equation (135) predicts values for Q that agree with values measured by more direct means to within a few parts percent, even though the flow pattern is not really steady at all. The other device is the pitot tube, which is illustrated in Figure 5B-->
The other device is the pitot tube, which is illustrated in Figure 5B--> . The fluid streamlines divide as they approach the blunt end of this tube, and at the point marked Q in the diagram there is complete stagnation, since the fluid at this point is moving neither up nor down nor to the right. It follows immediately from Bernoulli's law that
. The fluid streamlines divide as they approach the blunt end of this tube, and at the point marked Q in the diagram there is complete stagnation, since the fluid at this point is moving neither up nor down nor to the right. It follows immediately from Bernoulli's law that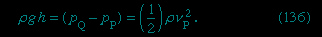
As with the venturi tube, one should therefore be able to find vP from the level difference h.
One other simple result deserves mention here. It concerns a jet of fluid emerging through a hole in the wall of a vessel filled with liquid under pressure. Observation of jets shows that after emerging they narrow slightly before settling down to a more or less uniform cross section known as the vena contracta. They do so because the streamlines are converging on the hole inside the vessel and are obliged to continue converging for a short while outside. It was Torricelli (Torricelli's theorem) who first suggested that, if the pressure excess inside the vessel is generated by a head of liquid h, then the velocity v at the vena contracta is the velocity that a free particle would reach on falling through a height h—i.e., that

This result is an immediate consequence, for an inviscid fluid, of the principle of energy conservation that Bernoulli's law enshrines.
In the following section, Bernoulli's law is used in an indirect way to establish a formula for the speed at which disturbances travel over the surface of shallow water. The explanation of several interesting phenomena having to do with water waves is buried in this formula. Analogous phenomena dealing with sound waves in gases are discussed below in Compressible flow in gases (fluid mechanics), where an alternative form of Bernoulli's law is introduced. This form of the law is restricted to gases in steady flow but is not restricted to flow velocities that are much less than the speed of sound. The complication that viscosity represents is again ignored throughout these two sections.
Waves on shallow water
 Imagine a layer of water with a flat base that has a small step on its surface, dividing a region in which the depth of the water is uniformly equal to D from a region in which it is uniformly equal to D(1 + ε), with ε \\<\\< 1. Let the water in the shallower region flow toward the step with some uniform speed V, as Figure 6A-->
Imagine a layer of water with a flat base that has a small step on its surface, dividing a region in which the depth of the water is uniformly equal to D from a region in which it is uniformly equal to D(1 + ε), with ε \\<\\< 1. Let the water in the shallower region flow toward the step with some uniform speed V, as Figure 6A--> suggests, and let this speed be just sufficient to hold the step in the same position so that the flow pattern is a steady one. The continuity condition (i.e., the condition that as much water flows out to the left per unit time as flows in from the right) indicates that in the deeper region the speed of the water is V(1 + ε)−1. Hence by applying Bernoulli's law to the points marked P and Q in the diagram, which lie on the same streamline and at both of which the pressure is atmospheric, one may deduce that
suggests, and let this speed be just sufficient to hold the step in the same position so that the flow pattern is a steady one. The continuity condition (i.e., the condition that as much water flows out to the left per unit time as flows in from the right) indicates that in the deeper region the speed of the water is V(1 + ε)−1. Hence by applying Bernoulli's law to the points marked P and Q in the diagram, which lie on the same streamline and at both of which the pressure is atmospheric, one may deduce that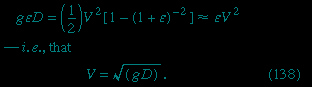
 Special Comp-->
Special Comp-->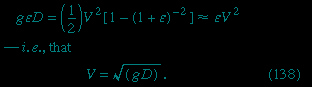 Special Comp-->
Special Comp-->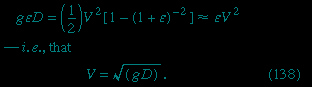 This result shows that, if the water in the shallower region is in fact stationary (see Figure 6B-->
This result shows that, if the water in the shallower region is in fact stationary (see Figure 6B--> ), the step advances over it with the speed V that equation (138-->
), the step advances over it with the speed V that equation (138-->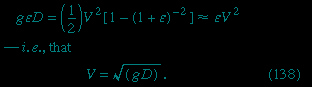 ) describes, and it reveals incidentally that behind the step the deeper water follows up with speed V【1 - (1 + ε)−1】 ≈ εV. The argument may readily be extended to disturbances of the surface that are undulatory rather than steplike. Provided that the distance between successive crests—a distance known as the wavelength and denoted by λ—is much greater than the depth of the water, D, and provided that its amplitude is very much less than D, a wave travels over stationary water at a speed given by (138-->
) describes, and it reveals incidentally that behind the step the deeper water follows up with speed V【1 - (1 + ε)−1】 ≈ εV. The argument may readily be extended to disturbances of the surface that are undulatory rather than steplike. Provided that the distance between successive crests—a distance known as the wavelength and denoted by λ—is much greater than the depth of the water, D, and provided that its amplitude is very much less than D, a wave travels over stationary water at a speed given by (138-->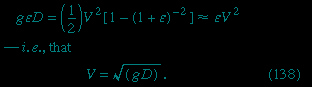 ). Because their speed does not depend on wavelength, the waves are said to be nondispersive.
). Because their speed does not depend on wavelength, the waves are said to be nondispersive.Evidently waves that are approaching a shelving beach should slow down as D diminishes. If they are approaching it at an angle, the slowing-down effect bends, or refracts, the wave crests so that they are nearly parallel to the shore by the time they ultimately break.
 Suppose now that a small step of height εD (ε \\<\\< 1) is traveling over stationary water of uniform depth D and that behind it is a second step of much the same height traveling in the same direction. Because the second step (suggested by a dotted line in Figure 6B-->
Suppose now that a small step of height εD (ε \\<\\< 1) is traveling over stationary water of uniform depth D and that behind it is a second step of much the same height traveling in the same direction. Because the second step (suggested by a dotted line in Figure 6B--> ) is traveling on a base that is moving at ε√(gD) and because the thickness of that base is (1 + ε)D rather than D, the speed of the second step is approximately (1 + 3ε/2)√(gD). Since this is greater than √(gD), the second step is bound to catch up with the first. Hence, if there are a succession of infinitesimal steps that raise the depth continuously from D to some value D′, which differs significantly from D, then the ramp on the surface is bound to become steeper as it advances. It may be shown that if D′ exceeds about 1.3D, the ramp ultimately becomes a vertical step of finite height and that the step then “breaks.” A finite step that has broken dissipates energy as heat in the resultant foaming motion, and Bernoulli's equation is no longer applicable to it. A simple argument based on conservation of momentum rather than energy, however, suffices to show that its velocity of propagation is
) is traveling on a base that is moving at ε√(gD) and because the thickness of that base is (1 + ε)D rather than D, the speed of the second step is approximately (1 + 3ε/2)√(gD). Since this is greater than √(gD), the second step is bound to catch up with the first. Hence, if there are a succession of infinitesimal steps that raise the depth continuously from D to some value D′, which differs significantly from D, then the ramp on the surface is bound to become steeper as it advances. It may be shown that if D′ exceeds about 1.3D, the ramp ultimately becomes a vertical step of finite height and that the step then “breaks.” A finite step that has broken dissipates energy as heat in the resultant foaming motion, and Bernoulli's equation is no longer applicable to it. A simple argument based on conservation of momentum rather than energy, however, suffices to show that its velocity of propagation is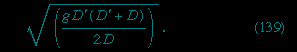
Tidal bores (bore), which may be observed on some estuaries, are examples on the large scale of the sort of phenomena to which (139-->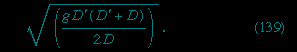 ) applies. Examples on a smaller scale include the hydraulic jumps that are commonly seen below weirs and sluice gates where a smooth stream of water suddenly rises at a foaming front. In this case, (139-->
) applies. Examples on a smaller scale include the hydraulic jumps that are commonly seen below weirs and sluice gates where a smooth stream of water suddenly rises at a foaming front. In this case, (139-->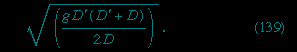 ) describes the speed of the water, since the front itself is more or less stationary.
) describes the speed of the water, since the front itself is more or less stationary.
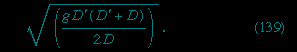 ) applies. Examples on a smaller scale include the hydraulic jumps that are commonly seen below weirs and sluice gates where a smooth stream of water suddenly rises at a foaming front. In this case, (139-->
) applies. Examples on a smaller scale include the hydraulic jumps that are commonly seen below weirs and sluice gates where a smooth stream of water suddenly rises at a foaming front. In this case, (139-->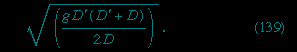 ) describes the speed of the water, since the front itself is more or less stationary.
) describes the speed of the water, since the front itself is more or less stationary. When water is shallow but not extremely shallow, so that correction terms of the order of (D/λ)2 are significant, waves of small amplitude become slightly dispersive (dispersion) (see below Waves on deep water (fluid mechanics)). In this case, a localized disturbance on the surface of a river or canal, which is guided by the banks in such a way that it can propagate in one direction only, is liable to spread as it propagates. If its amplitude is not small, however, the tendency to spread due to dispersion may in special circumstances be subtly balanced by the factors that cause waves of relatively large amplitude to form bores, and the result is a localized hump in the surface, of symmetrical shape, which does not spread at all. The phenomenon was first observed on a canal near Edinburgh in 1834 by a Scottish engineer named Scott Russell (Russell, John Scott); he later wrote a graphic account of following on horseback, for well over a kilometre, a “large solitary elevation . . . which continued its course along the channel apparently without change of form.” What Scott Russell saw is now called a soliton. Solitons on canals can have various widths, but the smaller the width the larger the height must be and the faster the soliton travels. Thus, if a high, narrow soliton is formed behind a low, broad one, it will catch up with the low one. It turns out that, when the high soliton does so, it passes through the low one and emerges with its shape unchanged (see Figure 7-->
When water is shallow but not extremely shallow, so that correction terms of the order of (D/λ)2 are significant, waves of small amplitude become slightly dispersive (dispersion) (see below Waves on deep water (fluid mechanics)). In this case, a localized disturbance on the surface of a river or canal, which is guided by the banks in such a way that it can propagate in one direction only, is liable to spread as it propagates. If its amplitude is not small, however, the tendency to spread due to dispersion may in special circumstances be subtly balanced by the factors that cause waves of relatively large amplitude to form bores, and the result is a localized hump in the surface, of symmetrical shape, which does not spread at all. The phenomenon was first observed on a canal near Edinburgh in 1834 by a Scottish engineer named Scott Russell (Russell, John Scott); he later wrote a graphic account of following on horseback, for well over a kilometre, a “large solitary elevation . . . which continued its course along the channel apparently without change of form.” What Scott Russell saw is now called a soliton. Solitons on canals can have various widths, but the smaller the width the larger the height must be and the faster the soliton travels. Thus, if a high, narrow soliton is formed behind a low, broad one, it will catch up with the low one. It turns out that, when the high soliton does so, it passes through the low one and emerges with its shape unchanged (see Figure 7--> ).
).It is now recognized that many of the nonlinear differential equations that appear in diverse branches of physics have solutions of large amplitude corresponding to solitons and that the remarkable capacity of solitons for surviving encounters with other solitons is universal. This discovery has stimulated much interest among mathematicians and physicists, and understanding of solitons is expanding rapidly.
Compressible flow in gases (gas)
Compressible flow refers to flow at velocities that are comparable to, or exceed, the speed of sound. The compressibility is relevant because at such velocities the variations in density that occur as the fluid moves from place to place cannot be ignored.
Suppose that the fluid is a gas at a low enough pressure for the ideal equation of state, equation (118-->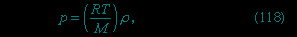 ), to apply and that its thermal conductivity is so poor that the compressions and rarefactions undergone by each element of the gas may be treated as adiabatic (see above). In this case, it follows from equation (120-->
), to apply and that its thermal conductivity is so poor that the compressions and rarefactions undergone by each element of the gas may be treated as adiabatic (see above). In this case, it follows from equation (120-->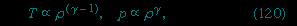 ) that the change of density accompanying any small change in pressure, dp, is such that
) that the change of density accompanying any small change in pressure, dp, is such that
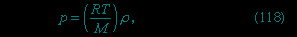 ), to apply and that its thermal conductivity is so poor that the compressions and rarefactions undergone by each element of the gas may be treated as adiabatic (see above). In this case, it follows from equation (120-->
), to apply and that its thermal conductivity is so poor that the compressions and rarefactions undergone by each element of the gas may be treated as adiabatic (see above). In this case, it follows from equation (120-->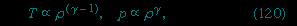 ) that the change of density accompanying any small change in pressure, dp, is such that
) that the change of density accompanying any small change in pressure, dp, is such that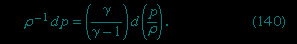
This makes it possible to integrate the right-hand side of equation (131-->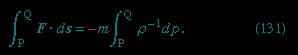 ), and one thereby arrives at a version of Bernoulli's law for a steady compressible flow of gases which states that
), and one thereby arrives at a version of Bernoulli's law for a steady compressible flow of gases which states that
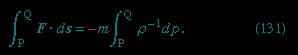 ), and one thereby arrives at a version of Bernoulli's law for a steady compressible flow of gases which states that
), and one thereby arrives at a version of Bernoulli's law for a steady compressible flow of gases which states that
is constant along a streamline. An equivalent statement is that
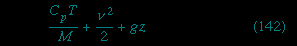
is constant along a streamline. It is worth noting that, when a gas flows through a nozzle or through a shock front (see below), the flow, though adiabatic, may not be reversible in the thermodynamic sense. Thus the entropy of the gas is not necessarily constant in such flow, and as a consequence the application of equation (120-->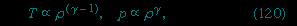 ) is open to question. Fortunately, the result expressed by (141-->
) is open to question. Fortunately, the result expressed by (141--> ) or (142-->
) or (142-->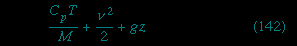 ) can be established by arguments that do not involve integration of (131-->
) can be established by arguments that do not involve integration of (131-->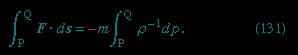 ). It is valid for steady adiabatic flow whether this is reversible or not.
). It is valid for steady adiabatic flow whether this is reversible or not.
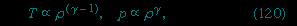 ) is open to question. Fortunately, the result expressed by (141-->
) is open to question. Fortunately, the result expressed by (141--> ) or (142-->
) or (142-->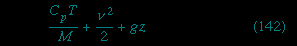 ) can be established by arguments that do not involve integration of (131-->
) can be established by arguments that do not involve integration of (131-->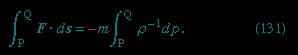 ). It is valid for steady adiabatic flow whether this is reversible or not.
). It is valid for steady adiabatic flow whether this is reversible or not.Bernoulli's law in the form of (142-->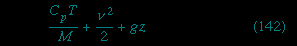 ) may be used to estimate the variation of temperature with height in the Earth's atmosphere. Even on the calmest day the atmosphere is normally in motion because convection currents (see below Convection (fluid mechanics)) are set up by heat derived from sunlight that is released at the Earth's surface. The currents are indeed adiabatic to a good approximation, and their velocity is generally small enough for the term v2 in (142-->
) may be used to estimate the variation of temperature with height in the Earth's atmosphere. Even on the calmest day the atmosphere is normally in motion because convection currents (see below Convection (fluid mechanics)) are set up by heat derived from sunlight that is released at the Earth's surface. The currents are indeed adiabatic to a good approximation, and their velocity is generally small enough for the term v2 in (142-->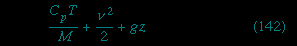 ) to be negligible. One can therefore deduce without more ado that the temperature of the atmosphere should fall off in a linear fashion—i.e., that
) to be negligible. One can therefore deduce without more ado that the temperature of the atmosphere should fall off in a linear fashion—i.e., that
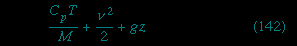 ) may be used to estimate the variation of temperature with height in the Earth's atmosphere. Even on the calmest day the atmosphere is normally in motion because convection currents (see below Convection (fluid mechanics)) are set up by heat derived from sunlight that is released at the Earth's surface. The currents are indeed adiabatic to a good approximation, and their velocity is generally small enough for the term v2 in (142-->
) may be used to estimate the variation of temperature with height in the Earth's atmosphere. Even on the calmest day the atmosphere is normally in motion because convection currents (see below Convection (fluid mechanics)) are set up by heat derived from sunlight that is released at the Earth's surface. The currents are indeed adiabatic to a good approximation, and their velocity is generally small enough for the term v2 in (142-->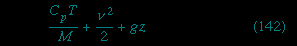 ) to be negligible. One can therefore deduce without more ado that the temperature of the atmosphere should fall off in a linear fashion—i.e., that
) to be negligible. One can therefore deduce without more ado that the temperature of the atmosphere should fall off in a linear fashion—i.e., that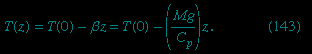
Here β is used to represent the temperature lapse rate, and the value suggested for this quantity, (Mg/Cp), is close to 10° C per kilometre for dry air.
This prediction is not exactly fulfilled in practice. Within the troposphere (i.e., to the heights of about 10 kilometres to which convection currents extend), the mean temperature does decrease with height in a linear fashion, but β is only about 6.5° C per kilometre. It is the water vapour in the atmosphere, which condenses as the air rises and cools, that lowers the lapse rate to this value by increasing the effective value of Cp. The fact that the lapse rate is smaller for moist air than for dry air means that a stream of moist air which passes over a mountain range and which deposits its moisture as rain or snow at the summit is warmer when it descends to sea level on the other side of the range than it was when it started. The foehn wind of the Alps owes its warmth to this effect.
The variation of the pressure of the atmosphere with height may be estimated in terms of β, using the equation
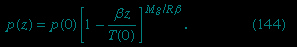
This is obtained by integration of (123--> ), using (118-->
), using (118-->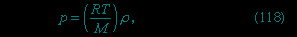 ) and (143-->
) and (143-->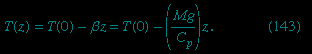 ).
).
 ), using (118-->
), using (118-->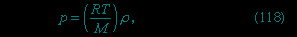 ) and (143-->
) and (143-->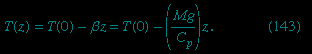 ).
).Special Comp-->
 In the form of equation (141-->
In the form of equation (141--> ), Bernoulli's law may be used to calculate the speed (speed of sound) of sound in gases. The argument is directly analogous to the one applied in the previous section to waves on shallow water—and, indeed, the diagrams in Figure 6-->
), Bernoulli's law may be used to calculate the speed (speed of sound) of sound in gases. The argument is directly analogous to the one applied in the previous section to waves on shallow water—and, indeed, the diagrams in Figure 6--> can serve to illustrate the argument here too, if they are regarded as plots of gas density (or else of pressure or temperature, which go hand in hand with density in adiabatic flow) versus position. The results of the argument will be stated without proof. If there exists an infinitesimal step in the density of the gas, it will remain stationary provided that the gas flows uniformly through it toward the region of higher density, with a velocity
can serve to illustrate the argument here too, if they are regarded as plots of gas density (or else of pressure or temperature, which go hand in hand with density in adiabatic flow) versus position. The results of the argument will be stated without proof. If there exists an infinitesimal step in the density of the gas, it will remain stationary provided that the gas flows uniformly through it toward the region of higher density, with a velocity

 In the form of equation (141-->
In the form of equation (141--> ), Bernoulli's law may be used to calculate the speed (speed of sound) of sound in gases. The argument is directly analogous to the one applied in the previous section to waves on shallow water—and, indeed, the diagrams in Figure 6-->
), Bernoulli's law may be used to calculate the speed (speed of sound) of sound in gases. The argument is directly analogous to the one applied in the previous section to waves on shallow water—and, indeed, the diagrams in Figure 6--> can serve to illustrate the argument here too, if they are regarded as plots of gas density (or else of pressure or temperature, which go hand in hand with density in adiabatic flow) versus position. The results of the argument will be stated without proof. If there exists an infinitesimal step in the density of the gas, it will remain stationary provided that the gas flows uniformly through it toward the region of higher density, with a velocity
can serve to illustrate the argument here too, if they are regarded as plots of gas density (or else of pressure or temperature, which go hand in hand with density in adiabatic flow) versus position. The results of the argument will be stated without proof. If there exists an infinitesimal step in the density of the gas, it will remain stationary provided that the gas flows uniformly through it toward the region of higher density, with a velocity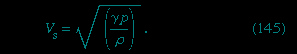
If the gas is stationary, then (145-->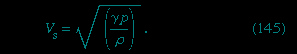 ) describes the velocity with which the step moves. It also describes the speed of propagation of the sort of undulatory variation of density that constitutes a sound wave of fixed frequency or pitch. Because the speed of sound is independent of pitch, sound waves, like waves on shallow water, are nondispersive. This is just as well. It is only because there is no dispersion that one can understand the words of a distant speaker or listen to a symphony orchestra with pleasure from the back of an auditorium as well as from the front.
) describes the velocity with which the step moves. It also describes the speed of propagation of the sort of undulatory variation of density that constitutes a sound wave of fixed frequency or pitch. Because the speed of sound is independent of pitch, sound waves, like waves on shallow water, are nondispersive. This is just as well. It is only because there is no dispersion that one can understand the words of a distant speaker or listen to a symphony orchestra with pleasure from the back of an auditorium as well as from the front.
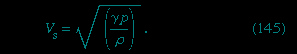 ) describes the velocity with which the step moves. It also describes the speed of propagation of the sort of undulatory variation of density that constitutes a sound wave of fixed frequency or pitch. Because the speed of sound is independent of pitch, sound waves, like waves on shallow water, are nondispersive. This is just as well. It is only because there is no dispersion that one can understand the words of a distant speaker or listen to a symphony orchestra with pleasure from the back of an auditorium as well as from the front.
) describes the velocity with which the step moves. It also describes the speed of propagation of the sort of undulatory variation of density that constitutes a sound wave of fixed frequency or pitch. Because the speed of sound is independent of pitch, sound waves, like waves on shallow water, are nondispersive. This is just as well. It is only because there is no dispersion that one can understand the words of a distant speaker or listen to a symphony orchestra with pleasure from the back of an auditorium as well as from the front.It should be noted that the formula for the speed of sound in gases may be proved in other ways, and Newton came close to it a century before Bernoulli's time. However, because Newton failed to appreciate the distinction between adiabatic and isothermal flow, his answer lacked the factor γ occurring in (145-->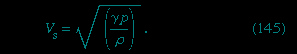 ). The first person to correct this error was Pierre-Simon Laplace (Laplace, Pierre-Simon, marquis de).
). The first person to correct this error was Pierre-Simon Laplace (Laplace, Pierre-Simon, marquis de).
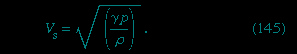 ). The first person to correct this error was Pierre-Simon Laplace (Laplace, Pierre-Simon, marquis de).
). The first person to correct this error was Pierre-Simon Laplace (Laplace, Pierre-Simon, marquis de).The above statements apply to density steps or undulations, the amplitude of which is infinitesimal, and they need some modification if the amplitude is large. In the first place it is found, as for waves on shallow water and for very much the same reasons, that, where two small density steps are moving parallel to one another, the second is bound to catch up with the first. It follows that, if there exists a propagating region in which the density rises in a continuous fashion from ρ to ρ′, where (ρ′ - ρ) is not necessarily small, then the width of this region is bound to diminish as time passes. Ultimately a shock (shock wave) front develops over which the density—and hence the pressure and temperature—rises almost discontinuously. There are processes within the shock front, vaguely analogous on the molecular scale to the foaming of a breaking water wave, by which energy is dissipated as heat. The speed of propagation, Vsh, of a shock front in a gas that is stationary in front of it may be expressed in terms of Vs and Vs′, the velocities of small-amplitude sound waves in front of the shock and behind it, respectively, by the equation

Thus, if the shock is a strong one (ρ′ \\>\\> ρ), Vsh may be significantly greater than both Vs and Vs′.
Even the gentlest sound wave, in which density and pressure initially oscillate in a smooth and sinusoidal fashion, develops into a succession of weak shock fronts in time. More noticeable shock fronts are a feature of the flow of gases at supersonic speeds through the nozzles of jet engines and accompany projectiles that are moving through stationary air at supersonic speeds. In certain circumstances when a supersonic aircraft is following a curved path, the accompanying shock wave may accidentally reinforce itself in places and thereby become offensively noticeable as a “ sonic boom,” which may break windowpanes and cause other damage. Strong shock fronts also occur immediately after explosions, of course, and when windowpanes are broken by an explosion, the broken glass tends to fall outward rather than inward. Such is the case because the glass is sucked out by the relatively low density and pressure that succeed the shock itself.
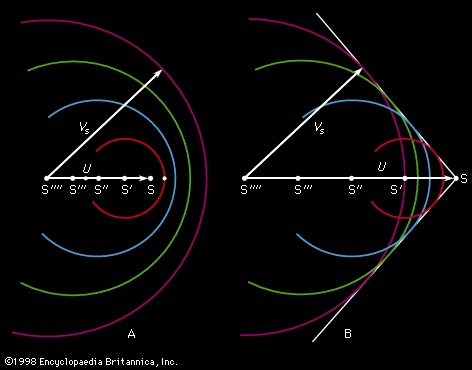


 The diagrams in Figure 8-->
The diagrams in Figure 8--> show a well-known construction attributed to the Austrian physicist Ernst Mach (Mach, Ernst) that explains the origin of the shock front accompanying a supersonic projectile. The circular arcs in this figure represent cross sections through spherical disturbances that are spreading with speed Vs from centres (S′, S″, etc.), which mark the position of the moving source S at the time when they were emitted. If the source is something like the tip of an arrow, which disturbs the air by parting it as it travels along but which is inaudible when stationary, then each “disturbance” due to some infinitesimal displacement of the tip is a spherical shell of infinitesimal thickness within which a small radial velocity has been imparted to the air. There is an infinite number of such disturbances, overlapping one another, of which only a handful are represented in Figure 8-->
show a well-known construction attributed to the Austrian physicist Ernst Mach (Mach, Ernst) that explains the origin of the shock front accompanying a supersonic projectile. The circular arcs in this figure represent cross sections through spherical disturbances that are spreading with speed Vs from centres (S′, S″, etc.), which mark the position of the moving source S at the time when they were emitted. If the source is something like the tip of an arrow, which disturbs the air by parting it as it travels along but which is inaudible when stationary, then each “disturbance” due to some infinitesimal displacement of the tip is a spherical shell of infinitesimal thickness within which a small radial velocity has been imparted to the air. There is an infinite number of such disturbances, overlapping one another, of which only a handful are represented in Figure 8--> . When the velocity of the source, U, is less than Vs (Figure 8A-->
. When the velocity of the source, U, is less than Vs (Figure 8A--> ), the result of adding them together is the sort of steady backflow that is to be expected around a moving obstacle, and there is no sound emission in the normal sense; the source remains inaudible. When U exceeds Vs, however, the spherical disturbances reinforce one another, as Figure 8B-->
), the result of adding them together is the sort of steady backflow that is to be expected around a moving obstacle, and there is no sound emission in the normal sense; the source remains inaudible. When U exceeds Vs, however, the spherical disturbances reinforce one another, as Figure 8B--> shows, on a conical caustic surface, which makes an angle of sin−1 (U/V) to the line of travel of the source, and it is on this surface that a shock front is to be expected. The cone becomes sharper as the source speeds up.
shows, on a conical caustic surface, which makes an angle of sin−1 (U/V) to the line of travel of the source, and it is on this surface that a shock front is to be expected. The cone becomes sharper as the source speeds up. viscosity
As shown above, a number of phenomena of considerable physical interest can be discussed using little more than the law of conservation of energy, as expressed by Bernoulli's law. However, the argument has so far been restricted to cases of steady flow. To discuss cases in which the flow is not steady, an equation of motion for fluids is needed, and one cannot write down a realistic equation of motion without facing up to the problems presented by viscosity, which have so far been deliberately set aside.
Stresses in laminar motion

 The concept of viscosity was first formalized by Newton (Newton, Sir Isaac), who considered the shear stresses (shear stress) likely to arise when a fluid undergoes what is called laminar motion (laminar flow) with the sort of velocity profile that is suggested in Figure 9A-->
The concept of viscosity was first formalized by Newton (Newton, Sir Isaac), who considered the shear stresses (shear stress) likely to arise when a fluid undergoes what is called laminar motion (laminar flow) with the sort of velocity profile that is suggested in Figure 9A--> ; the laminae here are planes normal to the x2-axis, and they are moving in the direction of the x1-axis with a velocity v1, which increases in a linear fashion with x2. Newton suggested that, as each lamina slips over the one below, it exerts a sort of frictional force upon the latter in the forward direction, in which case the upper lamina is bound to experience an equal reaction in the backward direction. The strength of these forces per unit area constitutes the component of shear stress normally written as σ12 (not to be confused with surface tension, for which the symbol σ has been used above). Figure 9B-->
; the laminae here are planes normal to the x2-axis, and they are moving in the direction of the x1-axis with a velocity v1, which increases in a linear fashion with x2. Newton suggested that, as each lamina slips over the one below, it exerts a sort of frictional force upon the latter in the forward direction, in which case the upper lamina is bound to experience an equal reaction in the backward direction. The strength of these forces per unit area constitutes the component of shear stress normally written as σ12 (not to be confused with surface tension, for which the symbol σ has been used above). Figure 9B--> shows, in elevation, an enlarged view of an infinitesimal element of the fluid of cubic shape, and the directions of the forces experienced by this cube associated with σ12 are indicated by arrows. Other arrows show the directions of the forces associated with the so-called normal stresses σ11 and σ22, which in the absence of motion of the fluid would both be equal, by Pascal's law (Pascal's principle), to -p. Now σ12 is clearly zero when the rate of variation of velocity, ∂v1/∂x2, is zero, for then there is no slip, and presumably it increases monotonically as ∂v1/∂x2 increases. Newton made the plausible assumption that the two are linearly related—i.e., that
shows, in elevation, an enlarged view of an infinitesimal element of the fluid of cubic shape, and the directions of the forces experienced by this cube associated with σ12 are indicated by arrows. Other arrows show the directions of the forces associated with the so-called normal stresses σ11 and σ22, which in the absence of motion of the fluid would both be equal, by Pascal's law (Pascal's principle), to -p. Now σ12 is clearly zero when the rate of variation of velocity, ∂v1/∂x2, is zero, for then there is no slip, and presumably it increases monotonically as ∂v1/∂x2 increases. Newton made the plausible assumption that the two are linearly related—i.e., that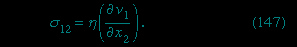
The full name for the coefficient η is shear viscosity to distinguish it from the bulk viscosity, b, which is defined below. The word shear, however, is frequently omitted in this context.
 Special Comp-->
Special Comp-->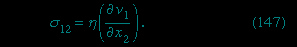 Now if the only shear stress acting on the cubic element of fluid sketched in Figure 9B-->
Now if the only shear stress acting on the cubic element of fluid sketched in Figure 9B--> were σ12, the cube would experience a torque tending to make it twist in a clockwise sense. Since the magnitude of the torque would vary like the third power of the linear dimensions of the cube, whereas the moment of inertia of the element would vary like the fifth power, the resultant angular acceleration for an infinitesimal cube would be infinite. One may infer that any tendency to twist in a clockwise sense gives rise instantaneously to an additional shear stress σ21, the direction of which is indicated in the diagram, and that σ12 and σ21 are equal at all times. It follows that equation (147-->
were σ12, the cube would experience a torque tending to make it twist in a clockwise sense. Since the magnitude of the torque would vary like the third power of the linear dimensions of the cube, whereas the moment of inertia of the element would vary like the fifth power, the resultant angular acceleration for an infinitesimal cube would be infinite. One may infer that any tendency to twist in a clockwise sense gives rise instantaneously to an additional shear stress σ21, the direction of which is indicated in the diagram, and that σ12 and σ21 are equal at all times. It follows that equation (147-->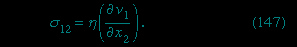 ) cannot be a complete expression for these shear stresses, for it does not include the possibility that the fluid is moving in the x2 direction, with a velocity v2 that varies with x1. The complete expression for what is called a Newtonian fluid is
) cannot be a complete expression for these shear stresses, for it does not include the possibility that the fluid is moving in the x2 direction, with a velocity v2 that varies with x1. The complete expression for what is called a Newtonian fluid is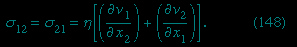
Similar expressions may be written down for σ23 (= σ32) and σ31 (= σ13). Since Newton's day these hypothetical expressions have been fully substantiated for gases and simple liquids, not only by experiment but also by analysis of the molecular motions and molecular interactions in such fluids undergoing shear, and for such fluids one can even predict the magnitude of η with reasonable success. There do exist, however, more complicated fluids for which the Newtonian description of shear stress is inadequate, and some of these are very familiar in the home. In the whites of eggs, for example, and in most shampoos, there are long-chain molecules that become entangled with one another, and entanglement may hinder their efforts to respond to changes of environment associated with flow. As a result, the stresses acting in such fluids may reflect the deformations experienced by the fluid in the recent past as much as the instantaneous rate of deformation. Moreover, the relation between stress and rate of deformation may be far from linear. Non-Newtonian effects, interesting though they are, lie outside the scope of the present discussion, however.

 The sort of velocity profile that is suggested by Figure 9B-->
The sort of velocity profile that is suggested by Figure 9B--> may be established by containing the fluid between two parallel flat plates and moving one plate relative to the other. The possibility exists that in this situation the layers of fluid immediately in contact with each plate will slip over them with some finite velocity (indicated in the diagram by an arrow labeled vslip). If so, the frictional stresses associated with this slip must be such as to balance the shear stress η(∂v1/∂x2) exerted on each of these layers by the rest of the fluid. Little is known about fluid-solid frictional stresses, but intelligent guesswork suggests that they are proportional in magnitude to vslip and that, in the circumstances to which Figure 9A-->
may be established by containing the fluid between two parallel flat plates and moving one plate relative to the other. The possibility exists that in this situation the layers of fluid immediately in contact with each plate will slip over them with some finite velocity (indicated in the diagram by an arrow labeled vslip). If so, the frictional stresses associated with this slip must be such as to balance the shear stress η(∂v1/∂x2) exerted on each of these layers by the rest of the fluid. Little is known about fluid-solid frictional stresses, but intelligent guesswork suggests that they are proportional in magnitude to vslip and that, in the circumstances to which Figure 9A--> refers, the distance d below the surface of the stationary bottom plate at which the straight line representing the variation of v1 with x2 extrapolates to zero should be of the same order of magnitude as the diameter of a molecule if the fluid is a liquid or as the molecular “mean free path” if it is a gas. These distances are normally very small compared with the separation of the plates, D. Accordingly, fluid flow patterns may normally be treated as subject to the boundary condition that at a fluid-solid interface the relative velocity of the fluid is zero. No reliable evidence for failure of predictions based on this no-slip boundary condition has yet been found, except in the case of what is called Knudsen flow of gases (i.e., flow at such low pressures that the mean free path is comparable in length with the dimensions of the apparatus).
refers, the distance d below the surface of the stationary bottom plate at which the straight line representing the variation of v1 with x2 extrapolates to zero should be of the same order of magnitude as the diameter of a molecule if the fluid is a liquid or as the molecular “mean free path” if it is a gas. These distances are normally very small compared with the separation of the plates, D. Accordingly, fluid flow patterns may normally be treated as subject to the boundary condition that at a fluid-solid interface the relative velocity of the fluid is zero. No reliable evidence for failure of predictions based on this no-slip boundary condition has yet been found, except in the case of what is called Knudsen flow of gases (i.e., flow at such low pressures that the mean free path is comparable in length with the dimensions of the apparatus). If a fluid is flowing steadily between two parallel plates that are both stationary and if its velocity must be zero in contact with both of them, the velocity profile must necessarily have the form indicated in Figure 10-->
If a fluid is flowing steadily between two parallel plates that are both stationary and if its velocity must be zero in contact with both of them, the velocity profile must necessarily have the form indicated in Figure 10--> . A force in the forward direction due to the shear stress η(∂v1/∂x2) is transmitted to the plates, and an equal force in the backward direction acts on the fluid. The motion therefore cannot be maintained unless the pressure acting on the fluid is greater on the left of the diagram than it is on the right. A full analysis shows the velocity profile to be parabolic, and it indicates that the rate of discharge is related to the pressure gradient by the equation
. A force in the forward direction due to the shear stress η(∂v1/∂x2) is transmitted to the plates, and an equal force in the backward direction acts on the fluid. The motion therefore cannot be maintained unless the pressure acting on the fluid is greater on the left of the diagram than it is on the right. A full analysis shows the velocity profile to be parabolic, and it indicates that the rate of discharge is related to the pressure gradient by the equation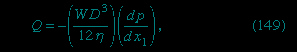

 where W ( \\>\\> D) is the width of the plates, measured perpendicular to the diagram in Figure 10-->
where W ( \\>\\> D) is the width of the plates, measured perpendicular to the diagram in Figure 10--> . A similar analysis of the problem of steady flow through a (horizontal) cylindrical pipe of uniform diameter D, to which Figure 10-->
. A similar analysis of the problem of steady flow through a (horizontal) cylindrical pipe of uniform diameter D, to which Figure 10--> could equally well apply, shows the rate of discharge in this case to be given by
could equally well apply, shows the rate of discharge in this case to be given by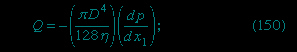
this famous result is known as Poiseuille's equation, and the type of flow to which it refers is called Poiseuille flow.
Bulk viscosity
Viscosity may affect the normal stress components, σ11, σ22, and σ33, as well as the shear stress components. To see why this is so, one needs to examine the way in which stress components transform when one's reference axes are rotated. Here, the result will be stated without proof that the general expression for σ11 consistent with (148-->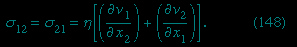 ) is
) is
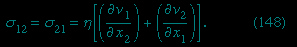 ) is
) is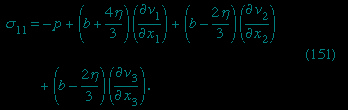
On the right-hand side of this equation, p represents the equilibrium pressure defined in terms of local density and temperature by the equation of state, and b is another viscosity coefficient known as the bulk viscosity.
The bulk viscosity is relevant only where the density is changing. Thus it plays a role in attenuating sound waves in fluids and may be estimated from the magnitude of the attenuation. If the fluid is effectively incompressible, however, so that changes of density may be ignored, the flow is everywhere subject to the continuity condition that
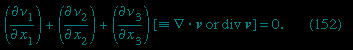
The terms in (151-->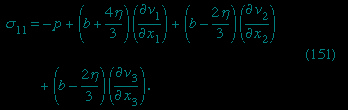 ) that involve b then cancel, and the expression simplifies to
) that involve b then cancel, and the expression simplifies to
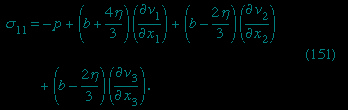 ) that involve b then cancel, and the expression simplifies to
) that involve b then cancel, and the expression simplifies to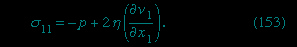
Similar equations may be written down for σ22 and σ33. These simpler expressions provide the basis for the argument that follows, and the bulk viscosity can be left on one side.
Measurement of shear viscosity
A variety of methods are available for the measurement of shear viscosity. One standard method involves measurement of the pressure gradient along a pipe for various rates of flow and application of Poiseuille's equation. Other methods involve measurement either of the damping of the torsional oscillations of a solid disk supported between two parallel plates when fluid is admitted to the space between the plates, or of the effect of the fluid on the frequency of the oscillations.
The Couette viscometer deserves a fuller explanation. In this device, the fluid occupies the space between two coaxial cylinders of radii a and b (\\> a); the outer cylinder is rotated with uniform angular velocity ω0, and the resultant torque transmitted to the inner stationary cylinder is measured. If both the terms on the right-hand side of equation (148-->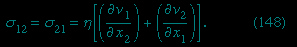 ) are taken into account, the shear stress in the circulating fluid is found to be proportional to r(dω/dr) rather than to (dv/dr)—not an unexpected result, since it is only if ω, the angular velocity of the fluid, varies with radius r that there is any slip between one cylindrical lamina of fluid and the next. The torque transmitted through the fluid is therefore proportional to r3(dω/dr). In the steady state, the opposing torques acting on the inner and outer surfaces of each cylindrical lamina of fluid must be of equal magnitude—otherwise the laminae accelerate—and this means that r3(dω/dr) must be independent of r. There are two basic modes of motion for a circulating fluid that satisfy this condition: in one, the liquid rotates as a solid body would, with an angular velocity that does not vary with r, and the torque is everywhere zero; in the other, ω varies like r−2. The angular velocity of the fluid in a Couette viscometer can be viewed as a mixture of these two modes in proportions that satisfy the boundary conditions at r = a and r = b. The torque transmitted per unit length of the cylinders turns out to be given by
) are taken into account, the shear stress in the circulating fluid is found to be proportional to r(dω/dr) rather than to (dv/dr)—not an unexpected result, since it is only if ω, the angular velocity of the fluid, varies with radius r that there is any slip between one cylindrical lamina of fluid and the next. The torque transmitted through the fluid is therefore proportional to r3(dω/dr). In the steady state, the opposing torques acting on the inner and outer surfaces of each cylindrical lamina of fluid must be of equal magnitude—otherwise the laminae accelerate—and this means that r3(dω/dr) must be independent of r. There are two basic modes of motion for a circulating fluid that satisfy this condition: in one, the liquid rotates as a solid body would, with an angular velocity that does not vary with r, and the torque is everywhere zero; in the other, ω varies like r−2. The angular velocity of the fluid in a Couette viscometer can be viewed as a mixture of these two modes in proportions that satisfy the boundary conditions at r = a and r = b. The torque transmitted per unit length of the cylinders turns out to be given by
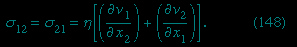 ) are taken into account, the shear stress in the circulating fluid is found to be proportional to r(dω/dr) rather than to (dv/dr)—not an unexpected result, since it is only if ω, the angular velocity of the fluid, varies with radius r that there is any slip between one cylindrical lamina of fluid and the next. The torque transmitted through the fluid is therefore proportional to r3(dω/dr). In the steady state, the opposing torques acting on the inner and outer surfaces of each cylindrical lamina of fluid must be of equal magnitude—otherwise the laminae accelerate—and this means that r3(dω/dr) must be independent of r. There are two basic modes of motion for a circulating fluid that satisfy this condition: in one, the liquid rotates as a solid body would, with an angular velocity that does not vary with r, and the torque is everywhere zero; in the other, ω varies like r−2. The angular velocity of the fluid in a Couette viscometer can be viewed as a mixture of these two modes in proportions that satisfy the boundary conditions at r = a and r = b. The torque transmitted per unit length of the cylinders turns out to be given by
) are taken into account, the shear stress in the circulating fluid is found to be proportional to r(dω/dr) rather than to (dv/dr)—not an unexpected result, since it is only if ω, the angular velocity of the fluid, varies with radius r that there is any slip between one cylindrical lamina of fluid and the next. The torque transmitted through the fluid is therefore proportional to r3(dω/dr). In the steady state, the opposing torques acting on the inner and outer surfaces of each cylindrical lamina of fluid must be of equal magnitude—otherwise the laminae accelerate—and this means that r3(dω/dr) must be independent of r. There are two basic modes of motion for a circulating fluid that satisfy this condition: in one, the liquid rotates as a solid body would, with an angular velocity that does not vary with r, and the torque is everywhere zero; in the other, ω varies like r−2. The angular velocity of the fluid in a Couette viscometer can be viewed as a mixture of these two modes in proportions that satisfy the boundary conditions at r = a and r = b. The torque transmitted per unit length of the cylinders turns out to be given by
It may be added that if the inner cylinder is absent, the steady flow pattern consists only of the first mode—i.e., the fluid rotates like a solid body with uniform angular velocity ω0. If the outer cylinder is absent, however, and the inner one rotates, it then consists only of the second mode. The angular velocity falls off like r−2, and the velocity v falls off like r−1.
In the equation of motion given in the following section, the shear viscosity occurs only in the combination (η/ρ). This combination occurs so frequently in arguments of fluid dynamics that it has been given a special name—kinetic viscosity. The kinetic viscosity at normal temperatures and pressures is about 10−6 square metre per second for water and about 1.5 × 10−5 square metre per second for air.
Navier-stokes equation
 One may have a situation where σ11 increases with x1. The force that this component of stress exerts on the right-hand side of the cubic element of fluid sketched in Figure 9B-->
One may have a situation where σ11 increases with x1. The force that this component of stress exerts on the right-hand side of the cubic element of fluid sketched in Figure 9B--> will then be greater than the force in the opposite direction that it exerts on the left-hand side, and the difference between the two will cause the fluid to accelerate along x1. Accelerations along x1 will also result if σ12 and σ13 increase with x2 and x3, respectively. These accelerations, and corresponding accelerations in the other two directions, are described by the equation of motion of the fluid. For a fluid moving so slowly compared with the speed of sound that it may be treated as incompressible and in which the variations of temperature from place to place are insufficient to cause significant variations in the shear viscosity η, this equation takes the form
will then be greater than the force in the opposite direction that it exerts on the left-hand side, and the difference between the two will cause the fluid to accelerate along x1. Accelerations along x1 will also result if σ12 and σ13 increase with x2 and x3, respectively. These accelerations, and corresponding accelerations in the other two directions, are described by the equation of motion of the fluid. For a fluid moving so slowly compared with the speed of sound that it may be treated as incompressible and in which the variations of temperature from place to place are insufficient to cause significant variations in the shear viscosity η, this equation takes the form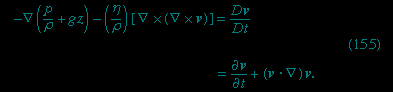
Euler derived all the terms in this equation except the one on the left-hand side proportional to (η/ρ), and without that term the equation is known as the Euler equation. The whole is called the Navier-Stokes equation.
The equation is written in a compact vector notation which many readers will find totally impenetrable, but a few words of explanation may help some others. The symbol ∇ represents the gradient operator, which, when preceding a scalar quantity X, generates a vector with components (∂X/∂x1, ∂X/∂x2, ∂X/∂x3). The vector product of this operator and the fluid velocity v—i.e., (∇ × v)—is sometimes designated as curl v 【and ∇ × (∇ × v) is also curl curl v】. Another name for (∇ × v), which expresses particularly vividly the characteristics of the local flow pattern that it represents, is vorticity. In a sample of fluid that is rotating like a solid body with uniform angular velocity ω0, the vorticity lies in the same direction as the axis of rotation, and its magnitude is equal to 2ω0. In other circumstances the vorticity is related in a similar fashion to the local angular velocity and may vary from place to place. As for the right-hand side of (155-->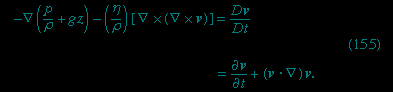 ), Dv/Dt represents the rate of change of velocity that one would see if the motion of a single element of the fluid could be followed—that is, it represents the acceleration of the element—while ∂v/∂t represents the rate of change at a fixed point in space. If the flow is steady, then ∂v/∂t is everywhere zero, but the fluid may be accelerating all the same, as individual fluid elements move from regions where the streamlines are widely spaced to regions where they are close together. It is the difference between Dv/Dt and ∂v/∂t—i.e., the final (v · ∇)v term in (155-->
), Dv/Dt represents the rate of change of velocity that one would see if the motion of a single element of the fluid could be followed—that is, it represents the acceleration of the element—while ∂v/∂t represents the rate of change at a fixed point in space. If the flow is steady, then ∂v/∂t is everywhere zero, but the fluid may be accelerating all the same, as individual fluid elements move from regions where the streamlines are widely spaced to regions where they are close together. It is the difference between Dv/Dt and ∂v/∂t—i.e., the final (v · ∇)v term in (155-->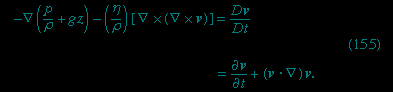 )—that introduces into fluid dynamics the nonlinearity that makes the subject so rife with surprises.
)—that introduces into fluid dynamics the nonlinearity that makes the subject so rife with surprises.
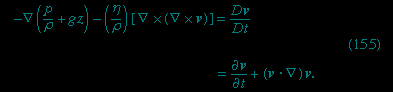 ), Dv/Dt represents the rate of change of velocity that one would see if the motion of a single element of the fluid could be followed—that is, it represents the acceleration of the element—while ∂v/∂t represents the rate of change at a fixed point in space. If the flow is steady, then ∂v/∂t is everywhere zero, but the fluid may be accelerating all the same, as individual fluid elements move from regions where the streamlines are widely spaced to regions where they are close together. It is the difference between Dv/Dt and ∂v/∂t—i.e., the final (v · ∇)v term in (155-->
), Dv/Dt represents the rate of change of velocity that one would see if the motion of a single element of the fluid could be followed—that is, it represents the acceleration of the element—while ∂v/∂t represents the rate of change at a fixed point in space. If the flow is steady, then ∂v/∂t is everywhere zero, but the fluid may be accelerating all the same, as individual fluid elements move from regions where the streamlines are widely spaced to regions where they are close together. It is the difference between Dv/Dt and ∂v/∂t—i.e., the final (v · ∇)v term in (155-->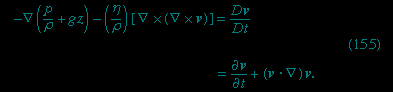 )—that introduces into fluid dynamics the nonlinearity that makes the subject so rife with surprises.
)—that introduces into fluid dynamics the nonlinearity that makes the subject so rife with surprises.Potential flow
This section is concerned with an important class of flow problems in which the vorticity is everywhere zero, and for such problems the Navier-Stokes equation may be greatly simplified. For one thing, the viscosity term drops out of it. For another, the nonlinear term, (v · ∇)v, may be transformed into ∇(v2/2). Finally, it may be shown that, when (∇ × v) is zero, one may describe the velocity by means of a scalar potential ϕ, using the equation

Thus (155-->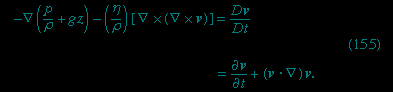 ) becomes
) becomes
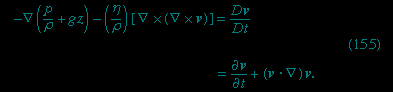 ) becomes
) becomes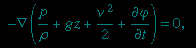
which may at once be integrated to show that

This result incorporates Bernoulli's law for an effectively incompressible fluid (【133-->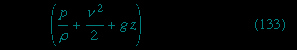 】), as was to be expected from the disappearance of the viscosity term. It is more powerful than (133-->
】), as was to be expected from the disappearance of the viscosity term. It is more powerful than (133-->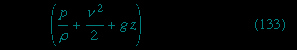 ), however, because it can be applied to nonsteady flow in which ∂ϕ/∂t is not zero and because it shows that in cases of potential flow the left-hand side of (157-->
), however, because it can be applied to nonsteady flow in which ∂ϕ/∂t is not zero and because it shows that in cases of potential flow the left-hand side of (157--> ) is constant everywhere and not just constant along each streamline.
) is constant everywhere and not just constant along each streamline.
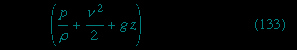 】), as was to be expected from the disappearance of the viscosity term. It is more powerful than (133-->
】), as was to be expected from the disappearance of the viscosity term. It is more powerful than (133-->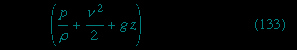 ), however, because it can be applied to nonsteady flow in which ∂ϕ/∂t is not zero and because it shows that in cases of potential flow the left-hand side of (157-->
), however, because it can be applied to nonsteady flow in which ∂ϕ/∂t is not zero and because it shows that in cases of potential flow the left-hand side of (157--> ) is constant everywhere and not just constant along each streamline.
) is constant everywhere and not just constant along each streamline.Vorticity-free, or potential, flow would be of rather limited interest were it not for the theorem, first proved by Thomson (Kelvin, William Thomson, Baron), that, in a body of fluid which is free of vorticity initially, the vorticity remains zero as the fluid moves. This theorem seems to open the door for relatively painless solutions to a great range of problems. Consider, for example, a stream of fluid in uniform motion approaching an obstacle of some sort. Well upstream of the obstacle the fluid is certainly vorticity-free, so it should, according to Thomson's theorem, be vorticity-free around the obstacle and downstream as well. In this case a flow potential should exist; and, if the fluid is effectively incompressible, it follows from equations (152-->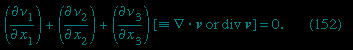 ) and (156-->
) and (156--> ) that it satisfies Laplace's equation,
) that it satisfies Laplace's equation,
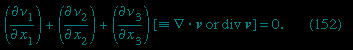 ) and (156-->
) and (156--> ) that it satisfies Laplace's equation,
) that it satisfies Laplace's equation,
This is perhaps the most frequently occurring differential equation in physics, and methods for solving it, subject to appropriate boundary conditions, are very well established. Given a solution for ϕ, the fluid velocity v follows at once, and one may then discover how the pressure varies with position and time from equation (157--> ).
).
 ).
). The physicists and mathematicians who developed fluid dynamics during the 19th century relied heavily on this reasoning. They based splendid achievements upon it, a notable example being the theory of waves on deep water (see below). There was a touch of unreality, however, about some of their theorizing. If carried to extremes, the argument of the previous section implies that water initially stationary in a beaker can never be set into rotation by rotating the beaker or by stirring it with a spoon, and this is clearly nonsense. It suggests that vorticity-free water remains vorticity-free if it is squeezed into a narrow pipe, and this too is plainly nonsensical, for the well-established parabolic profile illustrated by Figure 10-->
The physicists and mathematicians who developed fluid dynamics during the 19th century relied heavily on this reasoning. They based splendid achievements upon it, a notable example being the theory of waves on deep water (see below). There was a touch of unreality, however, about some of their theorizing. If carried to extremes, the argument of the previous section implies that water initially stationary in a beaker can never be set into rotation by rotating the beaker or by stirring it with a spoon, and this is clearly nonsense. It suggests that vorticity-free water remains vorticity-free if it is squeezed into a narrow pipe, and this too is plainly nonsensical, for the well-established parabolic profile illustrated by Figure 10--> is not vorticity-free. What is misleading about the argument in situations like these is that it pays inadequate attention to what happens at interfaces. Following the work of Prandtl, physicists now appreciate that vorticity is liable to be fed into the fluid at interfaces, whether these are interfaces between the fluid and some solid object or the free surfaces of a liquid. Once the slightest trace of vorticity is present, it destroys the conditions on which the proof of Thomson's theorem depends. Moreover, vorticity admitted at interfaces spreads into the fluid in much the same way that a dye would spread, and whether or not the results of potential theory are useful depends on how much of the fluid is contaminated in the particular circumstances under discussion.
is not vorticity-free. What is misleading about the argument in situations like these is that it pays inadequate attention to what happens at interfaces. Following the work of Prandtl, physicists now appreciate that vorticity is liable to be fed into the fluid at interfaces, whether these are interfaces between the fluid and some solid object or the free surfaces of a liquid. Once the slightest trace of vorticity is present, it destroys the conditions on which the proof of Thomson's theorem depends. Moreover, vorticity admitted at interfaces spreads into the fluid in much the same way that a dye would spread, and whether or not the results of potential theory are useful depends on how much of the fluid is contaminated in the particular circumstances under discussion.Potential flow with circulation: vortex lines
The proof of Thomson's theorem depends on the concept of circulation, which Thomson introduced. This quantity is defined for a closed loop which is embedded in, and moves with, the fluid; denoted by K, it is the integral around the loop of v · dl, where dl is an element of length along the loop. If the vorticity is everywhere zero, then so is the circulation around all possible loops, and vice versa. Thomson showed that K cannot change if the viscous term in (155-->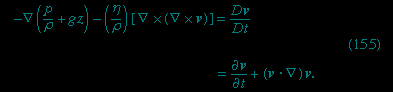 ) contributes nothing to the local acceleration, and it follows that both K and vorticity remain zero for all time.
) contributes nothing to the local acceleration, and it follows that both K and vorticity remain zero for all time.
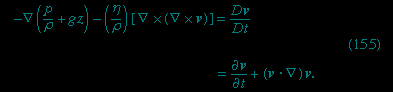 ) contributes nothing to the local acceleration, and it follows that both K and vorticity remain zero for all time.
) contributes nothing to the local acceleration, and it follows that both K and vorticity remain zero for all time.Reference was made earlier to the sort of steady flow pattern that may be set up by rotating a cylindrical spindle in a fluid; the streamlines are circles around the spindle, and the velocity falls off like r−1. This pattern of flow occurs naturally in whirlpools (whirlpool) and typhoons (typhoon), where the role of the spindle is played by a “core” in which the fluid rotates like a solid body; the axis around which the fluid circulates is then referred to as a vortex line. Each small element of fluid outside the core, if examined in isolation for a short interval of time, appears to be undergoing translation without rotation, and the local vorticity is zero. Were it not so, the viscous torques would not cancel and the flow pattern would not be a steady one. Nevertheless, the circulation is not zero if the loop for which it is defined is one that encloses the spindle or core. In such situations, a potential that obeys Laplace's equation outside the spindle or core can be found, but it is no longer, to use a technical term that may be familiar to some readers, single-valued.
Readers who recognize this term are likely to have encountered it in the context of electromagnetism, and it is worth remarking that all the results of potential flow theory have electromagnetic analogues, in which streamlines become the lines of force of a magnetic field and vortex lines become lines of electric current. The analogy may be illustrated by reference to the Magnus effect.
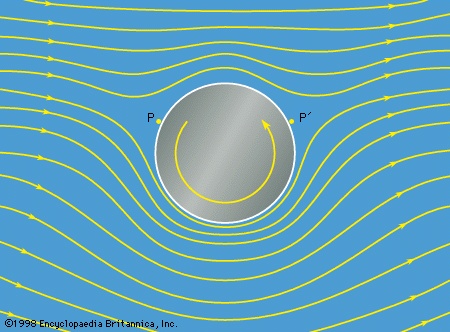 This effect (named for the German physicist and chemist H.G. Magnus, who first investigated it experimentally) arises when fluid flows steadily past a cylindrical spindle, with a velocity that at large distances from the spindle is perpendicular to the spindle's axis and uniformly equal to, say, v0, while the spindle itself is steadily rotated. Rotation is communicated to the fluid, and in the steady state the circulation around any loop that encloses the spindle (and encloses a layer of fluid adjacent to the spindle within which the vorticity is nonzero and potential theory is inapplicable) has some nonzero value K. The streamlines that describe the steady flow pattern (outside that “boundary layer”) have the form suggested by Figure 11-->
This effect (named for the German physicist and chemist H.G. Magnus, who first investigated it experimentally) arises when fluid flows steadily past a cylindrical spindle, with a velocity that at large distances from the spindle is perpendicular to the spindle's axis and uniformly equal to, say, v0, while the spindle itself is steadily rotated. Rotation is communicated to the fluid, and in the steady state the circulation around any loop that encloses the spindle (and encloses a layer of fluid adjacent to the spindle within which the vorticity is nonzero and potential theory is inapplicable) has some nonzero value K. The streamlines that describe the steady flow pattern (outside that “boundary layer”) have the form suggested by Figure 11--> , though the details naturally depend on the magnitude of v0 and K. The flow pattern has stagnation points at P and P′ and, since the pressure is high at such points, the spindle may be expected to experience a downward force perpendicular both to its axis and to the direction of v0. Detailed calculations confirm this expectation and show that the magnitude of the force, per unit length of the spindle, is
, though the details naturally depend on the magnitude of v0 and K. The flow pattern has stagnation points at P and P′ and, since the pressure is high at such points, the spindle may be expected to experience a downward force perpendicular both to its axis and to the direction of v0. Detailed calculations confirm this expectation and show that the magnitude of the force, per unit length of the spindle, is
This so-called Magnus force is directly analogous to the force that a transverse magnetic field B0 exerts upon a wire carrying an electric current I, the magnitude of which, per unit length of the wire, is B0I.
The Magnus force on rotating cylinders has been utilized to propel experimental yachts, and it is closely related to the lift force on airfoils that enables airplanes to fly (see below Lift (fluid mechanics)). The transverse forces that cause spinning balls to swerve in flight are, however, not Magnus forces, as is sometimes asserted. They are due to the asymmetrical nature of the eddies that develop at the rear of a spinning sphere (see below Boundary layers and separation (fluid mechanics)). cricket balls, unlike the balls used for baseball, tennis, and golf, have a raised equatorial seam that plays an important part in making the eddies asymmetric. A bowler in cricket who wants to make the ball swerve imparts spin to it, but he does so chiefly to ensure that the orientation of this seam remains steady as the ball moves toward the batsman.
It may be shown, by reference to the magnetic analogue or in other ways, that straight vortex lines of equal but opposite strength, ±K, which are parallel and separated by a distance d, will drift sideways together through the fluid at a speed given by K/2πd. Similarly, a vortex line that has joined up on itself to form a closed vortex ring of radius a drifts along its axis with a speed given by
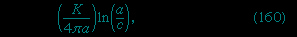
where c is the radius of the line's core, with ln standing for natural logarithm. This formula applies, for example, to smoke rings. The fact that such rings slow down as they propagate can be explained in terms of the increase of c with time, due to viscosity.
Waves on deep water
One particular solution of Laplace's equation that describes wave motion on the surface of a lake or of the ocean is

In this case the x-axis is the direction of propagation and the z-axis is vertical; z = 0 describes the free surface of the water when it is undisturbed and z = −D describes the bottom surface; ϕ0 is an arbitrary constant that determines the amplitude of the motion; and f is the frequency of the waves and λ their wavelength. If λ is more than a few centimetres, surface tension is irrelevant and the pressure in the liquid just below its free surface is atmospheric for all values of x. It can be shown that in these circumstances the wave motion described by (161--> ) is consistent with (157-->
) is consistent with (157--> ) only if the frequency and wavelength are related by the equation
) only if the frequency and wavelength are related by the equation
 ) is consistent with (157-->
) is consistent with (157--> ) only if the frequency and wavelength are related by the equation
) only if the frequency and wavelength are related by the equation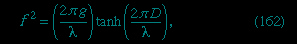
and an expression for the speed of the waves may be deduced from this, since V = fλ. For shallow water (D \\<\\< λ) one obtains the answer already quoted as equation (138-->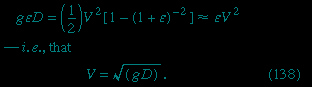 ), but for deep water (D \\>\\> λ) the answer is
), but for deep water (D \\>\\> λ) the answer is
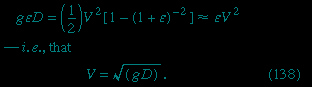 ), but for deep water (D \\>\\> λ) the answer is
), but for deep water (D \\>\\> λ) the answer is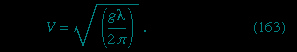
Waves on deep water are evidently dispersive (dispersion), and surfers rely on this fact. A storm in the middle of the ocean disturbs the surface in a chaotic way that would be useless for surfing, but as the component waves travel toward the shore they separate; those with long wavelengths move ahead of those with short wavelengths because they travel faster. As a result, the waves seem nicely regular by the time that they arrive.
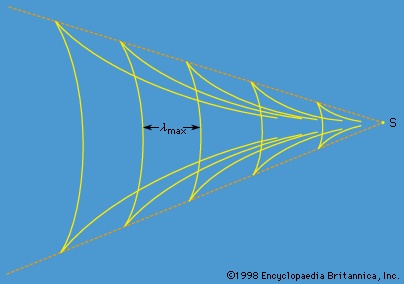
 Anyone who has observed the waves behind a moving ship will know that they are confined to a V-shaped area of the water's surface, with the ship at its apex. The waves are particularly prominent on the arms of the V, but they can also be discerned between these arms where the wave crests curve in the manner indicated in Figure 12-->
Anyone who has observed the waves behind a moving ship will know that they are confined to a V-shaped area of the water's surface, with the ship at its apex. The waves are particularly prominent on the arms of the V, but they can also be discerned between these arms where the wave crests curve in the manner indicated in Figure 12--> . It seems to be widely believed that the angle of the V becomes more acute as the boat speeds up, much in the way that the conical shock wave accompanying a supersonic projectile becomes more acute (see Figure 8-->
. It seems to be widely believed that the angle of the V becomes more acute as the boat speeds up, much in the way that the conical shock wave accompanying a supersonic projectile becomes more acute (see Figure 8--> ). That is not the case; the dispersive character of waves on deep water is such that the V has a fixed angle of 2 sin−1(1/3) = 39°. Thomson (Lord Kelvin) was the first to explain this, and so the V-shaped area is now known as the Kelvin wedge.
). That is not the case; the dispersive character of waves on deep water is such that the V has a fixed angle of 2 sin−1(1/3) = 39°. Thomson (Lord Kelvin) was the first to explain this, and so the V-shaped area is now known as the Kelvin wedge.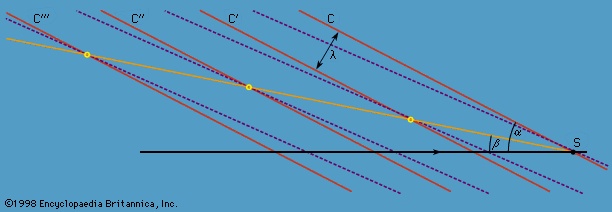 A version of Thomson's argument is illustrated by the diagram in Figure 13-->
A version of Thomson's argument is illustrated by the diagram in Figure 13--> . Here S (the “source”) represents the bow of the ship which is moving from left to right with uniform speed U, and the lines labeled C, C′, C″, etc., represent a set of parallel wave crests which are also moving from left to right. It can be shown that S will create this set of crests if, but only if, it rides continuously on the one labeled C. (It also can be shown that, though the crests in the set continue indefinitely to the left of C, there can be none to the right of this one.) The condition that S and C move together indicates that there is a relation between wavelength λ and inclination α expressed by the equation
. Here S (the “source”) represents the bow of the ship which is moving from left to right with uniform speed U, and the lines labeled C, C′, C″, etc., represent a set of parallel wave crests which are also moving from left to right. It can be shown that S will create this set of crests if, but only if, it rides continuously on the one labeled C. (It also can be shown that, though the crests in the set continue indefinitely to the left of C, there can be none to the right of this one.) The condition that S and C move together indicates that there is a relation between wavelength λ and inclination α expressed by the equation
This condition can evidently be satisfied by many other sets of crests besides the one represented by full lines in the figure—e.g., by the set with slightly shorter wavelength λ′ that is represented by broken lines. When one takes into consideration all the sets that satisfy (164--> ) and have wavelengths intermediate between λ and λ′, it becomes apparent that over most of the area behind the source they interfere destructively. They reinforce one another, however, near the intersections that are ringed in the figure. These intersections lie on a line through S of inclination β, where
) and have wavelengths intermediate between λ and λ′, it becomes apparent that over most of the area behind the source they interfere destructively. They reinforce one another, however, near the intersections that are ringed in the figure. These intersections lie on a line through S of inclination β, where
 ) and have wavelengths intermediate between λ and λ′, it becomes apparent that over most of the area behind the source they interfere destructively. They reinforce one another, however, near the intersections that are ringed in the figure. These intersections lie on a line through S of inclination β, where
) and have wavelengths intermediate between λ and λ′, it becomes apparent that over most of the area behind the source they interfere destructively. They reinforce one another, however, near the intersections that are ringed in the figure. These intersections lie on a line through S of inclination β, where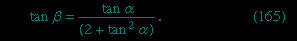
It follows that, though the angle α can take any value between 90° (corresponding to λ = λmax = 2πU2/g) and zero, tan β can never exceed 1/2√2, and sin β can never exceed 1/3.
Ships lose energy to the waves in the Kelvin wedge, and they experience additional resistance on that account. The resistance is particularly high when the wave system created by the bow, where water is pushed aside, reinforces the wave system created by the “anti-source” at the stern, where the water closes in again. Such reinforcement is liable to occur when the effective length of the boat, L, is equal to (2n + 1)λmax/2 (with n = 0, 1, 2, . . .) and therefore when the Froude number, U/√(Lg), takes one of the values 【 √((2n + 1)π) 】−1. However, once a boat has been accelerated past U = √(Lg/π), the bow and stern waves tend to cancel, and the resistance resulting from wave creation diminishes.
Waves on deep water whose wavelength is a few centimetres or less are generally referred to as ripples. In such waves, the pressure differences across the curved surface of the water associated with surface tension (see equation 【129-->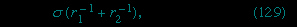 】) are not negligible, and the appropriate expression for their speed of propagation is
】) are not negligible, and the appropriate expression for their speed of propagation is
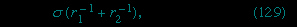 】) are not negligible, and the appropriate expression for their speed of propagation is
】) are not negligible, and the appropriate expression for their speed of propagation is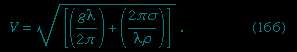
The wave velocity is therefore large for very short wavelengths as well as for very long ones. For water at normal temperatures, V has a minimum value of about 0.23 metre per second where the wavelength is about 17 millimetres, and it follows (note that equation 【164--> 】 has no real root for α unless U exceeds V) that an object moving through water can create no ripples at all unless its speed exceeds 0.23 metre per second. A wind moving over the surface of water likewise creates no ripples unless its speed exceeds a certain critical value, but this is a more complicated phenomenon, and the critical speed in question is distinctly higher.
】 has no real root for α unless U exceeds V) that an object moving through water can create no ripples at all unless its speed exceeds 0.23 metre per second. A wind moving over the surface of water likewise creates no ripples unless its speed exceeds a certain critical value, but this is a more complicated phenomenon, and the critical speed in question is distinctly higher.
 】 has no real root for α unless U exceeds V) that an object moving through water can create no ripples at all unless its speed exceeds 0.23 metre per second. A wind moving over the surface of water likewise creates no ripples unless its speed exceeds a certain critical value, but this is a more complicated phenomenon, and the critical speed in question is distinctly higher.
】 has no real root for α unless U exceeds V) that an object moving through water can create no ripples at all unless its speed exceeds 0.23 metre per second. A wind moving over the surface of water likewise creates no ripples unless its speed exceeds a certain critical value, but this is a more complicated phenomenon, and the critical speed in question is distinctly higher.Boundary layers (boundary layer) and separation
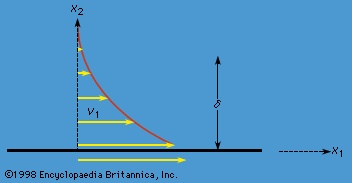 It should be reiterated that vorticity is liable to enter a fluid that is initially undergoing potential flow where it makes contact with a solid and also at its free surface. The way in which, having entered, it spreads, may be illustrated by a simple example. Consider a large body of fluid, initially stationary, being set into motion by the movement in its own plane of a large solid plate that is immersed within the fluid. The motion is communicated from solid to fluid by the frictional forces that prevent slip between the two (see above Viscosity (fluid mechanics)), and a velocity profile of the form suggested by Figure 14-->
It should be reiterated that vorticity is liable to enter a fluid that is initially undergoing potential flow where it makes contact with a solid and also at its free surface. The way in which, having entered, it spreads, may be illustrated by a simple example. Consider a large body of fluid, initially stationary, being set into motion by the movement in its own plane of a large solid plate that is immersed within the fluid. The motion is communicated from solid to fluid by the frictional forces that prevent slip between the two (see above Viscosity (fluid mechanics)), and a velocity profile of the form suggested by Figure 14--> is established. Its development with time turns out to be described by the partial differential equation
is established. Its development with time turns out to be described by the partial differential equation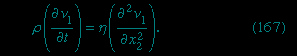
 Special Comp-->
Special Comp-->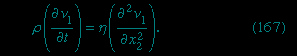 In this situation the vorticity, which may be denoted by the symbol Ω, has one nonzero component, directed along the axis perpendicular to the diagram in Figure 14-->
In this situation the vorticity, which may be denoted by the symbol Ω, has one nonzero component, directed along the axis perpendicular to the diagram in Figure 14--> ; it is Ω3 = -(∂v1/∂x2). Differentiation of (167-->
; it is Ω3 = -(∂v1/∂x2). Differentiation of (167-->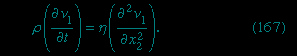 ) with respect to x2 shows at once that
) with respect to x2 shows at once that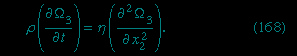
This is a diffusion equation. It indicates that, if the plate oscillates to and fro with frequency f, then the so-called boundary layer within which Ω3 is nonzero has a thickness δ given by
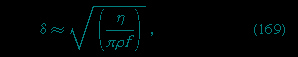
and in most instances of oscillatory motion this is small enough for the boundary layer to be neglected. For example, the boundary layer on the surface of the ocean has a thickness of less than one millimetre when a wave with a frequency of about one hertz passes by; because the effects of viscosity are confined to this layer, they are too slight to affect the propagation of the wave to any significant degree. If the plate is kept moving at a uniform rate, however, the thickness of the boundary layer, as described by (168-->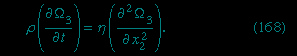 ), will increase with the time t that has elapsed since the motion of the plate began, according to the equation
), will increase with the time t that has elapsed since the motion of the plate began, according to the equation
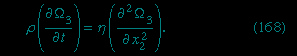 ), will increase with the time t that has elapsed since the motion of the plate began, according to the equation
), will increase with the time t that has elapsed since the motion of the plate began, according to the equation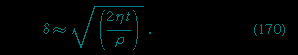
Prandtl (Prandtl, Ludwig) suggested that when a stream of fluid flows steadily past an obstacle of finite extent, such as a sphere, the time that matters is the time for which fluid on a streamline just outside the boundary layer remains in contact with it. This time is of order D/v0, where D is the diameter of the sphere and v0 is the speed of the fluid well upstream. Hence, one would expect the thickness of the boundary layer at the rear of the sphere to be something like
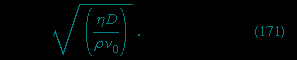
If the velocity v0 is so low that (170-->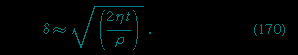 ) is comparable with or greater than the diameter D, the flow pattern must be so contaminated by vorticity that the neglect of viscosity and reliance on Bernoulli's equation and on the other results of potential theory is clearly unjustified. If the velocity is high and (171-->
) is comparable with or greater than the diameter D, the flow pattern must be so contaminated by vorticity that the neglect of viscosity and reliance on Bernoulli's equation and on the other results of potential theory is clearly unjustified. If the velocity is high and (171-->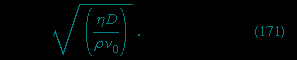 ) is much less than D, however, the boundary layer would seem to be of little importance. Surely then the results of potential theory are to be trusted?
) is much less than D, however, the boundary layer would seem to be of little importance. Surely then the results of potential theory are to be trusted?
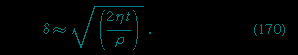 ) is comparable with or greater than the diameter D, the flow pattern must be so contaminated by vorticity that the neglect of viscosity and reliance on Bernoulli's equation and on the other results of potential theory is clearly unjustified. If the velocity is high and (171-->
) is comparable with or greater than the diameter D, the flow pattern must be so contaminated by vorticity that the neglect of viscosity and reliance on Bernoulli's equation and on the other results of potential theory is clearly unjustified. If the velocity is high and (171-->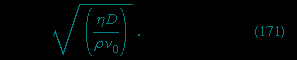 ) is much less than D, however, the boundary layer would seem to be of little importance. Surely then the results of potential theory are to be trusted?
) is much less than D, however, the boundary layer would seem to be of little importance. Surely then the results of potential theory are to be trusted?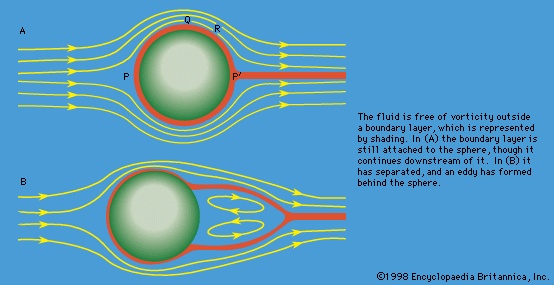
 Alas, that optimistic conclusion is not confirmed by experiment. What happens at high velocities is that the boundary layer comes unstuck from the surface of the sphere—it is said to separate. The reason why it does so is suggested by Figure 15A-->
Alas, that optimistic conclusion is not confirmed by experiment. What happens at high velocities is that the boundary layer comes unstuck from the surface of the sphere—it is said to separate. The reason why it does so is suggested by Figure 15A--> , which shows the streamlines to be expected when the boundary layer (shown in this figure by a shaded area still attached to the sphere) is relatively thin. Evidently the fluid velocity is higher near the equator of the sphere, at Q, than it is at either of the two poles, P and P′. Thus according to Bernoulli's equation, which can be relied on outside the boundary layer, the pressure near Q is less than it is near P and P′. The pressure gradient acts on the fluid in the boundary layer, accelerating it between P and Q but decelerating it between Q and P′. As the flow velocity increases, so does the pressure gradient, and at a certain stage the decelerating effect between Q and P′ becomes so large that the direction of flow within the boundary layer reverses in sign near the point labeled R in the diagram. The backflow of fluid near R causes an accumulation of fluid that obliges the oncoming boundary layer to separate, and the fluid behind the sphere circulates slowly within the boundary layer as a ring-shaped eddy (Figure 15B-->
, which shows the streamlines to be expected when the boundary layer (shown in this figure by a shaded area still attached to the sphere) is relatively thin. Evidently the fluid velocity is higher near the equator of the sphere, at Q, than it is at either of the two poles, P and P′. Thus according to Bernoulli's equation, which can be relied on outside the boundary layer, the pressure near Q is less than it is near P and P′. The pressure gradient acts on the fluid in the boundary layer, accelerating it between P and Q but decelerating it between Q and P′. As the flow velocity increases, so does the pressure gradient, and at a certain stage the decelerating effect between Q and P′ becomes so large that the direction of flow within the boundary layer reverses in sign near the point labeled R in the diagram. The backflow of fluid near R causes an accumulation of fluid that obliges the oncoming boundary layer to separate, and the fluid behind the sphere circulates slowly within the boundary layer as a ring-shaped eddy (Figure 15B--> ).
). The diagrams in Figure 15-->
The diagrams in Figure 15--> might well refer to a cylinder rather than a sphere. If such were the case, however, the regions of circulating flow behind the obstacle that are shown in the second diagram would form parts of two separate straight eddies instead of a single ring-shaped one. At high velocities the eddies behind a cylinder become so large that they are blown off by the current and disappear downstream while new eddies form in their place; they are said to have been shed. The top and bottom eddies are shed alternately, and the cylinder experiences an oscillating force as a consequence. If the cylinder is something flexible like a telephone or power cable, it will move to and fro under this force; the singing noise produced by cables in high winds is due to a resonance between their natural frequency of transverse oscillation and the frequency of eddy shedding. Similar processes are liable to occur behind obstacles of any shape, and the occurrence of eddies behind rocks or walls that interrupt the smooth flow of rivers is a familiar phenomenon.
might well refer to a cylinder rather than a sphere. If such were the case, however, the regions of circulating flow behind the obstacle that are shown in the second diagram would form parts of two separate straight eddies instead of a single ring-shaped one. At high velocities the eddies behind a cylinder become so large that they are blown off by the current and disappear downstream while new eddies form in their place; they are said to have been shed. The top and bottom eddies are shed alternately, and the cylinder experiences an oscillating force as a consequence. If the cylinder is something flexible like a telephone or power cable, it will move to and fro under this force; the singing noise produced by cables in high winds is due to a resonance between their natural frequency of transverse oscillation and the frequency of eddy shedding. Similar processes are liable to occur behind obstacles of any shape, and the occurrence of eddies behind rocks or walls that interrupt the smooth flow of rivers is a familiar phenomenon.Drag
A fluid stream exerts a drag force FD on any obstacle placed in its path, and the same force arises if the obstacle moves and the fluid is stationary. How large it is and how it may be reduced are questions of obvious importance to designers of moving vehicles of all sorts and equally to designers of cooling towers and other structures who want to be certain that the structures will not collapse in the face of winds.
An expression for the drag force on a sphere which is valid at such low velocities that the v2 term in the Navier-Stokes equation is negligible, and thus at velocities such that the boundary layer thickness described by (171-->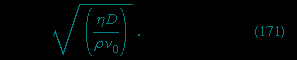 ) is larger than the sphere diameter D, was first obtained by Stokes (Stokes, Sir George Gabriel, 1st Baronet). Known as Stokes's law, it may be written as
) is larger than the sphere diameter D, was first obtained by Stokes (Stokes, Sir George Gabriel, 1st Baronet). Known as Stokes's law, it may be written as
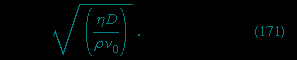 ) is larger than the sphere diameter D, was first obtained by Stokes (Stokes, Sir George Gabriel, 1st Baronet). Known as Stokes's law, it may be written as
) is larger than the sphere diameter D, was first obtained by Stokes (Stokes, Sir George Gabriel, 1st Baronet). Known as Stokes's law, it may be written as
One-third of this force is transmitted to the sphere by shear stresses near the equator, and the remaining two-thirds are due to the pressure being higher at the front of the sphere than at the rear.
As the velocity increases and the boundary layer decreases in thickness, the effect of the shear stresses (or of what is sometimes called skin friction in this context) becomes less and less important compared with the effect of the pressure difference. It is impossible to calculate that difference precisely, except in the limit to which Stokes's law applies, but there are grounds for expecting that once eddies have formed it is about ρv02/2. Hence at high velocities one may expect
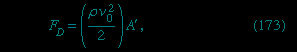
where A′ is some effective cross-sectional area, presumably comparable to its true cross-sectional area A (which is πD2/4 for a sphere) but not necessarily exactly equal to this. It is conventional to describe drag forces in terms of a dimensionless quantity called the drag coefficient; this is defined, irrespective of the shape of the body, as the ratio 【FD/(ρv02/2)A】 and is denoted by CD. At high velocities, CD is clearly the same thing as the ratio (A′/A) and should therefore be of order unity.
This is as far as theory can go with this problem. The principles of dimensional analysis can be invoked to show that, provided the compressibility of the fluid is irrelevant (i.e., provided the flow velocity is well below the speed of sound), the drag coefficient must be some universal function of another dimensionless quantity known as the Reynolds number and defined as

One must, however, resort to experiments to discover the form of this function. Fortunately, a limited number of experiments will suffice because the function is universal. They can be performed using whatever liquids and spheres are most convenient, provided that the whole range of R that is likely to be important is covered. Once the results have been plotted on a graph of CD versus R, the graph can be used to predict the drag forces experienced by other spheres in other liquids at velocities that may be quite different from those so far employed. This point is worth emphasizing because it enshrines the principle of dynamic similarity, which is heavily relied on by engineers whenever they use results obtained with models to predict the behaviour of much larger structures.
 The CD versus R curve for spheres, plotted with logarithmic scales, is shown in Figure 16-->
The CD versus R curve for spheres, plotted with logarithmic scales, is shown in Figure 16--> . Stokes's law, re-expressed in terms of CD and R, becomes CD = 24/R, and it is represented by the straight line on the left of the diagram. This law evidently fails when R exceeds about 1. There is a considerable range of R in the middle of the diagram over which CD is about 0.5, but when R reaches about 3 × 10−5 it falls dramatically, to about 0.1. The figure includes the corresponding curves for cylinders of diameter D whose axes are transverse to the direction of flow and for transverse disks of diameter D. The curve for cylinders is similar to that for spheres (though it has no straight-line part at low Reynolds number to correspond to Stokes's law), but the curve for disks is noticeably flatter. This flatness is linked to the fact that a disk has sharp edges around which the streamlines converge and diverge rapidly. The resulting large pressure gradients near the edge favour the formation and shedding of eddies. The drag force on a transverse flat plate of any shape can normally be estimated quite accurately, provided its edges are sharp, by assuming the drag coefficient to be unity.
. Stokes's law, re-expressed in terms of CD and R, becomes CD = 24/R, and it is represented by the straight line on the left of the diagram. This law evidently fails when R exceeds about 1. There is a considerable range of R in the middle of the diagram over which CD is about 0.5, but when R reaches about 3 × 10−5 it falls dramatically, to about 0.1. The figure includes the corresponding curves for cylinders of diameter D whose axes are transverse to the direction of flow and for transverse disks of diameter D. The curve for cylinders is similar to that for spheres (though it has no straight-line part at low Reynolds number to correspond to Stokes's law), but the curve for disks is noticeably flatter. This flatness is linked to the fact that a disk has sharp edges around which the streamlines converge and diverge rapidly. The resulting large pressure gradients near the edge favour the formation and shedding of eddies. The drag force on a transverse flat plate of any shape can normally be estimated quite accurately, provided its edges are sharp, by assuming the drag coefficient to be unity.



 Since sharp edges favour the formation and shedding of eddies, and thereby increase the drag coefficient, one may hope to reduce the drag coefficient by streamlining the obstacle. It is at the rear of the obstacle that separation occurs, and it is therefore the rear that needs streamlining. By stretching this out in the manner suggested in Figure 17A-->
Since sharp edges favour the formation and shedding of eddies, and thereby increase the drag coefficient, one may hope to reduce the drag coefficient by streamlining the obstacle. It is at the rear of the obstacle that separation occurs, and it is therefore the rear that needs streamlining. By stretching this out in the manner suggested in Figure 17A--> , the pressure gradient acting on the boundary layer behind the obstacle can be much reduced. Other methods of reducing drag that have some practical applications are illustrated in Figures 17B-->
, the pressure gradient acting on the boundary layer behind the obstacle can be much reduced. Other methods of reducing drag that have some practical applications are illustrated in Figures 17B--> and 17C-->
and 17C--> . In 17B-->
. In 17B--> the obstacle is the wing of an aircraft with a slot through its leading edge; the current of air channeled through this slot imparts forward momentum to the fluid in the boundary layer on the upper surface of the wing to hinder this fluid from moving backward. The cowls that are often fitted to the leading edges of aircraft wings have a similar purpose. In Figure 17C-->
the obstacle is the wing of an aircraft with a slot through its leading edge; the current of air channeled through this slot imparts forward momentum to the fluid in the boundary layer on the upper surface of the wing to hinder this fluid from moving backward. The cowls that are often fitted to the leading edges of aircraft wings have a similar purpose. In Figure 17C--> , the obstacle is equipped with an internal device—a pump of some sort—which prevents the accumulation of boundary-layer fluid that would otherwise lead to separation by sucking it in through small holes in the surface of the obstacle, near Q; the fluid may be ejected again through holes near P′, where it will do no harm.
, the obstacle is equipped with an internal device—a pump of some sort—which prevents the accumulation of boundary-layer fluid that would otherwise lead to separation by sucking it in through small holes in the surface of the obstacle, near Q; the fluid may be ejected again through holes near P′, where it will do no harm. It should be stressed that the curves in Figure 16-->
It should be stressed that the curves in Figure 16--> are universal only so long as the velocity v0 is much less than the speed of sound. When v0 is comparable with the speed of sound, VS, the compressibility of the fluid becomes relevant, which means that the drag coefficient has to be regarded as dependent on the dimensionless ratio M = v0/VS, known as the Mach number, as well as on the Reynolds number. The drag coefficient always rises as M approaches unity but may thereafter fall. To reduce drag in the supersonic region, it pays to streamline the front of obstacles or projectiles rather than the rear, as this reduces the intensity of the shock cone (see above Compressible flow in gases (fluid mechanics)).
are universal only so long as the velocity v0 is much less than the speed of sound. When v0 is comparable with the speed of sound, VS, the compressibility of the fluid becomes relevant, which means that the drag coefficient has to be regarded as dependent on the dimensionless ratio M = v0/VS, known as the Mach number, as well as on the Reynolds number. The drag coefficient always rises as M approaches unity but may thereafter fall. To reduce drag in the supersonic region, it pays to streamline the front of obstacles or projectiles rather than the rear, as this reduces the intensity of the shock cone (see above Compressible flow in gases (fluid mechanics)).Lift
If an aircraft wing, or airfoil, is to fulfill its function, it must experience an upward lift force, as well as a drag force, when the aircraft is in motion. The lift force arises because the speed at which the displaced air moves over the top of the airfoil (and over the top of the attached boundary layer) is greater than the speed at which it moves over the bottom and because the pressure acting on the airfoil from below is therefore greater than the pressure from above. It also can be seen, however, as an inevitable consequence of the finite circulation that exists around the airfoil. One way to establish circulation around an obstacle is to rotate it, as was seen earlier in the description of the Magnus effect. The circulation around an airfoil, however, is created by its forward motion; it arises as soon as the airfoil moves fast enough to shed its first eddy.


 The lift force on an airfoil moving through stationary air at a steady speed v0 is the same as the lift force on an identical airfoil that is stationary in air moving at v0 the other way; the latter is easier to represent pictorially. Figure 18A-->
The lift force on an airfoil moving through stationary air at a steady speed v0 is the same as the lift force on an identical airfoil that is stationary in air moving at v0 the other way; the latter is easier to represent pictorially. Figure 18A--> shows a set of streamlines representing potential flow past a stationary inclined plate before any eddy has been shed. The pattern is a symmetrical one, and the pressure variations associated with it generate neither drag nor lift. At the rear of the plate, however, the streamlines diverge rapidly, so conditions exist for the formation of an eddy there, and the sense of its rotation will be counterclockwise. It grows more easily and is shed more quickly because the edges of the plate are sharp. Figure 18B-->
shows a set of streamlines representing potential flow past a stationary inclined plate before any eddy has been shed. The pattern is a symmetrical one, and the pressure variations associated with it generate neither drag nor lift. At the rear of the plate, however, the streamlines diverge rapidly, so conditions exist for the formation of an eddy there, and the sense of its rotation will be counterclockwise. It grows more easily and is shed more quickly because the edges of the plate are sharp. Figure 18B--> shows some streamlines for the same plate a moment after shedding when the detached eddy, known as the starting vortex, is still in view. The circulation around the closed loop shown by a broken curve in this diagram was zero before the eddy formed and, according to Thomson's theorem (see above Potential flow (fluid mechanics)), it must still be zero. Passing through this loop, there thus must be a vortex line having clockwise circulation -K to compensate for the circulation +K of the starting vortex. This other line, known as the bound vortex, is not immediately apparent in the diagram because it is attached to the plate, and it remains thus attached as the starting vortex is swept away downstream. It does show up, however, in a modification of the flow pattern immediately behind the plate, where the streamlines no longer diverge as they do in Figure 18A-->
shows some streamlines for the same plate a moment after shedding when the detached eddy, known as the starting vortex, is still in view. The circulation around the closed loop shown by a broken curve in this diagram was zero before the eddy formed and, according to Thomson's theorem (see above Potential flow (fluid mechanics)), it must still be zero. Passing through this loop, there thus must be a vortex line having clockwise circulation -K to compensate for the circulation +K of the starting vortex. This other line, known as the bound vortex, is not immediately apparent in the diagram because it is attached to the plate, and it remains thus attached as the starting vortex is swept away downstream. It does show up, however, in a modification of the flow pattern immediately behind the plate, where the streamlines no longer diverge as they do in Figure 18A--> . Because the divergence here has been eliminated, no further eddies are likely to be formed.
. Because the divergence here has been eliminated, no further eddies are likely to be formed.

 Earlier, the formula ρv0K was quoted for the strength of the Magnus force per unit length of a rotating cylinder, and the same formula can be applied to the inclined plate in Figure 18B-->
Earlier, the formula ρv0K was quoted for the strength of the Magnus force per unit length of a rotating cylinder, and the same formula can be applied to the inclined plate in Figure 18B--> or to any airfoil that has shed a starting vortex and around which, consequently, there is circulation. The validity of the formula does not depend in any way on the precise shape of the airfoil, any more than the force exerted by a magnetic field on a wire carrying a current depends on the cross-sectional shape of the wire. The design of the airfoil, nevertheless, has a critical effect on the magnitude of the lift force because it determines the magnitude of K. The sort of cross section that is adopted for the wings of aircraft has been sketched already in Figure 17B-->
or to any airfoil that has shed a starting vortex and around which, consequently, there is circulation. The validity of the formula does not depend in any way on the precise shape of the airfoil, any more than the force exerted by a magnetic field on a wire carrying a current depends on the cross-sectional shape of the wire. The design of the airfoil, nevertheless, has a critical effect on the magnitude of the lift force because it determines the magnitude of K. The sort of cross section that is adopted for the wings of aircraft has been sketched already in Figure 17B--> . The rear edge is made as sharp as possible for reasons that have already been explained, and it may take the form of hinged flaps that are lowered at takeoff. Lowering the flaps increases K and therefore also the lift, but the flaps need to be raised when the aircraft has reached its cruising altitude because they cause undesirable drag. The circulation and the lift can also be increased by increasing the angle α (see Figure 17B-->
. The rear edge is made as sharp as possible for reasons that have already been explained, and it may take the form of hinged flaps that are lowered at takeoff. Lowering the flaps increases K and therefore also the lift, but the flaps need to be raised when the aircraft has reached its cruising altitude because they cause undesirable drag. The circulation and the lift can also be increased by increasing the angle α (see Figure 17B--> ) at which the main part of the airfoil is inclined to the direction of motion. There is a limit to the lift that can be generated in this way, however, for if the inclination is too great the boundary layer separates behind the wing's leading edge, and the bound vortex, on which the lift depends, may be shed as a result. The aircraft is then said to stall. The leading edge is made as smooth and rounded as possible to discourage stalling.
) at which the main part of the airfoil is inclined to the direction of motion. There is a limit to the lift that can be generated in this way, however, for if the inclination is too great the boundary layer separates behind the wing's leading edge, and the bound vortex, on which the lift depends, may be shed as a result. The aircraft is then said to stall. The leading edge is made as smooth and rounded as possible to discourage stalling.Thomson's theorem can be used to prove that if the airfoil is of finite length then the starting vortex and the bound vortex must both be parts of a single, continuous vortex ring. They are joined by two trailing vortices, which run backward from the ends of the airfoil. As time passes, these trailing vortices grow steadily longer, and more and more energy is needed to feed the swirling motion of the fluid around them. It is clear, at any rate in the case where the airfoil is moving and the air is stationary, that this energy can come only from whatever agency propels the airfoil forward, and hence that the trailing vortices are a source of additional drag. The magnitude of the additional drag is proportional to K2 but it does not increase, as the lift force does, if the airfoil is made longer while K is kept the same. For this reason, designers who wish to maximize the ratio of lift to drag will make the wings of their aircraft as long as they can—as long, that is, as is consistent with strength and rigidity requirements.
 When a yacht is sailing (sail) into the wind, its sail acts as an airfoil of which the mast is the leading edge, and the considerations that favour long wings for aircraft favour tall masts as well.
When a yacht is sailing (sail) into the wind, its sail acts as an airfoil of which the mast is the leading edge, and the considerations that favour long wings for aircraft favour tall masts as well.Turbulence (turbulent flow)
The nonlinear nature of the (v · ∇)v term in the Navier-Stokes equation—equation (155-->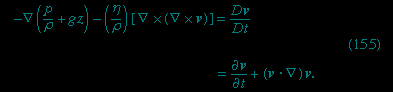 )—means that solutions of this equation cannot be superposed. The fact that v1(R, t) and v2(R, t) satisfy the equation does not ensure that (v1 + v2) does so too. The nonlinear term provides a contact, in fact, through which two different modes of motion may exchange energy, so that one grows in amplitude at the expense of the other. A great deal of experimental and theoretical work has shown, in particular, that if a fluid is undergoing regular laminar motion (of the sort that was discussed in connection with Poiseuille's law, for example) at sufficiently high rates of shear, small periodic perturbations of this motion are liable to grow parasitically. Perturbations on a smaller scale still grow parasitically on those that are first established, until the flow pattern is so grossly disturbed that it is no longer useful to define a fluid velocity for each point in space; the description of the flow has to be a statistical one in terms of mean values and of correlated fluctuations about the mean. The flow is then said to be turbulent.
)—means that solutions of this equation cannot be superposed. The fact that v1(R, t) and v2(R, t) satisfy the equation does not ensure that (v1 + v2) does so too. The nonlinear term provides a contact, in fact, through which two different modes of motion may exchange energy, so that one grows in amplitude at the expense of the other. A great deal of experimental and theoretical work has shown, in particular, that if a fluid is undergoing regular laminar motion (of the sort that was discussed in connection with Poiseuille's law, for example) at sufficiently high rates of shear, small periodic perturbations of this motion are liable to grow parasitically. Perturbations on a smaller scale still grow parasitically on those that are first established, until the flow pattern is so grossly disturbed that it is no longer useful to define a fluid velocity for each point in space; the description of the flow has to be a statistical one in terms of mean values and of correlated fluctuations about the mean. The flow is then said to be turbulent.
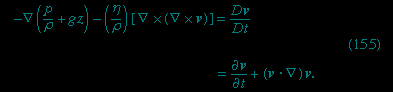 )—means that solutions of this equation cannot be superposed. The fact that v1(R, t) and v2(R, t) satisfy the equation does not ensure that (v1 + v2) does so too. The nonlinear term provides a contact, in fact, through which two different modes of motion may exchange energy, so that one grows in amplitude at the expense of the other. A great deal of experimental and theoretical work has shown, in particular, that if a fluid is undergoing regular laminar motion (of the sort that was discussed in connection with Poiseuille's law, for example) at sufficiently high rates of shear, small periodic perturbations of this motion are liable to grow parasitically. Perturbations on a smaller scale still grow parasitically on those that are first established, until the flow pattern is so grossly disturbed that it is no longer useful to define a fluid velocity for each point in space; the description of the flow has to be a statistical one in terms of mean values and of correlated fluctuations about the mean. The flow is then said to be turbulent.
)—means that solutions of this equation cannot be superposed. The fact that v1(R, t) and v2(R, t) satisfy the equation does not ensure that (v1 + v2) does so too. The nonlinear term provides a contact, in fact, through which two different modes of motion may exchange energy, so that one grows in amplitude at the expense of the other. A great deal of experimental and theoretical work has shown, in particular, that if a fluid is undergoing regular laminar motion (of the sort that was discussed in connection with Poiseuille's law, for example) at sufficiently high rates of shear, small periodic perturbations of this motion are liable to grow parasitically. Perturbations on a smaller scale still grow parasitically on those that are first established, until the flow pattern is so grossly disturbed that it is no longer useful to define a fluid velocity for each point in space; the description of the flow has to be a statistical one in terms of mean values and of correlated fluctuations about the mean. The flow is then said to be turbulent.In the case (to which Poiseuille's law applies) of laminar flow through a uniform cylindrical pipe of diameter D, turbulence inevitably sets in when the Reynolds number R reaches a critical value that is about 105; in this context, the Reynolds number is defined (compare equation 【174--> 】) as
】) as
 】) as
】) as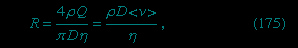
where Q is the rate of discharge and \\<v\\> is the mean fluid velocity. Turbulence sets in at much lower velocities, however, if the end of the pipe where the fluid enters is not carefully flared. The critical value of the Reynolds number for a pipe with a bluff entry may be as low as 2300, and this corresponds to a rate of discharge through a pipe for which D is, say, two centimetres, of only about three litres per minute. Thus pipe flow in engineering practice is more often turbulent than not. Once turbulence has set in, Q increases less rapidly with pressure gradient than Poiseuille's equation—equation (150-->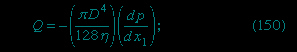 )—predicts; it increases roughly as the square root of the pressure gradient or slightly more rapidly than this if the internal surface of the pipe is very smooth.
)—predicts; it increases roughly as the square root of the pressure gradient or slightly more rapidly than this if the internal surface of the pipe is very smooth.
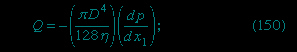 )—predicts; it increases roughly as the square root of the pressure gradient or slightly more rapidly than this if the internal surface of the pipe is very smooth.
)—predicts; it increases roughly as the square root of the pressure gradient or slightly more rapidly than this if the internal surface of the pipe is very smooth.
 Turbulence arises not only in pipes but also within boundary layers (boundary layer) around solid obstacles when the rate of shear within the boundary layer becomes large enough. Curiously enough, the onset of turbulence in the boundary layer can reduce the drag force on obstacles. In the case of a spherical obstacle, the point at which the boundary layer separates from the rear surface of the sphere shifts backward when the boundary layer becomes turbulent, away from the equator Q in Figure 15-->
Turbulence arises not only in pipes but also within boundary layers (boundary layer) around solid obstacles when the rate of shear within the boundary layer becomes large enough. Curiously enough, the onset of turbulence in the boundary layer can reduce the drag force on obstacles. In the case of a spherical obstacle, the point at which the boundary layer separates from the rear surface of the sphere shifts backward when the boundary layer becomes turbulent, away from the equator Q in Figure 15--> and toward P′, and the eddies attached to the sphere therefore become smaller. It is turbulence in the boundary layer that is responsible for the dramatic drop in the drag coefficient for both spheres and cylinders that occurs, as can be seen from Figure 16-->
and toward P′, and the eddies attached to the sphere therefore become smaller. It is turbulence in the boundary layer that is responsible for the dramatic drop in the drag coefficient for both spheres and cylinders that occurs, as can be seen from Figure 16--> , when the Reynolds number is about 3 × 105. This drop enables golf balls to travel farther than they would do otherwise, and the dimples on the surface of golf balls are meant to encourage turbulence in the boundary layer. If swimsuits with rough surfaces help swimmers to move faster, as has been claimed, the same explanation may apply.
, when the Reynolds number is about 3 × 105. This drop enables golf balls to travel farther than they would do otherwise, and the dimples on the surface of golf balls are meant to encourage turbulence in the boundary layer. If swimsuits with rough surfaces help swimmers to move faster, as has been claimed, the same explanation may apply.Where conditions for turbulence exist, flow rates of water through tubes may be increased and the drag forces exerted on obstacles by water diminished by dissolving small amounts of suitable polymers (polymer) in the water. This is surprising, because such additives increase viscosity, and in the preturbulent regime to which Poiseuille's law applies, their effect on the flow rate is quite the reverse. As has already been stated, the small perturbations that arise in a turbulent fluid tend to collapse into smaller perturbations and then into smaller perturbations still, until the motion is turbulent on a very fine scale—i.e., on the scale of molecular dimensions—and until the energy stored in the perturbations is finally dissipated as heat. Polymer molecules seem to have the effect they do because, over the relatively large distances to which each such molecule extends, they impose a coherence on the fluid motion that would not otherwise be present.
convection
Apart from some remarks in the above section Compressible flow in gases (fluid mechanics) about the circulation of the atmosphere, no attention has yet been paid to situations in which temperature differences are imposed upon a fluid by contact with hot and cold bodies. This subject will be briefly taken up here.
Consider first the case of two vertical plates with fluid between them, one at temperature T1 and the other at T2, in the presence of a vertical gravitational field. The hotter plate might be a domestic radiator and the colder plate the wall to which it is fixed. Thermal conduction ensures that the layer of air adjacent to the radiator is hotter than the rest of the air, and thermal expansion ensures that it is less dense. Consequently, the vertical pressure gradient which satisfies equation (123--> ) in the rest of the air is too large to keep the layer adjacent to the radiator in equilibrium; that layer rises and, similarly, the cold layer adjacent to the wall falls. A circulating pattern of thermal convection is thereby established, and, because this brings colder air (aerodynamics) into contact with the radiator, the rate at which heat is lost from the radiator is enhanced. The heat loss, once convection has been established, depends in a complicated manner on the separation between the plates (D) and on the thermal diffusivity (κ), specific heat, density, thermal expansion coefficient (α), and viscosity of the fluid. The heat loss also depends on (T1 - T2), of course, and it is worthwhile noting that the manner in which it does so is not linear; the heat loss increases more rapidly than the temperature difference. Newton's law of cooling, which postulates a linear relationship, is obeyed only in circumstances where convection is prevented or in circumstances where it is forced (when a radiator is fan-assisted, for example).
) in the rest of the air is too large to keep the layer adjacent to the radiator in equilibrium; that layer rises and, similarly, the cold layer adjacent to the wall falls. A circulating pattern of thermal convection is thereby established, and, because this brings colder air (aerodynamics) into contact with the radiator, the rate at which heat is lost from the radiator is enhanced. The heat loss, once convection has been established, depends in a complicated manner on the separation between the plates (D) and on the thermal diffusivity (κ), specific heat, density, thermal expansion coefficient (α), and viscosity of the fluid. The heat loss also depends on (T1 - T2), of course, and it is worthwhile noting that the manner in which it does so is not linear; the heat loss increases more rapidly than the temperature difference. Newton's law of cooling, which postulates a linear relationship, is obeyed only in circumstances where convection is prevented or in circumstances where it is forced (when a radiator is fan-assisted, for example).
 ) in the rest of the air is too large to keep the layer adjacent to the radiator in equilibrium; that layer rises and, similarly, the cold layer adjacent to the wall falls. A circulating pattern of thermal convection is thereby established, and, because this brings colder air (aerodynamics) into contact with the radiator, the rate at which heat is lost from the radiator is enhanced. The heat loss, once convection has been established, depends in a complicated manner on the separation between the plates (D) and on the thermal diffusivity (κ), specific heat, density, thermal expansion coefficient (α), and viscosity of the fluid. The heat loss also depends on (T1 - T2), of course, and it is worthwhile noting that the manner in which it does so is not linear; the heat loss increases more rapidly than the temperature difference. Newton's law of cooling, which postulates a linear relationship, is obeyed only in circumstances where convection is prevented or in circumstances where it is forced (when a radiator is fan-assisted, for example).
) in the rest of the air is too large to keep the layer adjacent to the radiator in equilibrium; that layer rises and, similarly, the cold layer adjacent to the wall falls. A circulating pattern of thermal convection is thereby established, and, because this brings colder air (aerodynamics) into contact with the radiator, the rate at which heat is lost from the radiator is enhanced. The heat loss, once convection has been established, depends in a complicated manner on the separation between the plates (D) and on the thermal diffusivity (κ), specific heat, density, thermal expansion coefficient (α), and viscosity of the fluid. The heat loss also depends on (T1 - T2), of course, and it is worthwhile noting that the manner in which it does so is not linear; the heat loss increases more rapidly than the temperature difference. Newton's law of cooling, which postulates a linear relationship, is obeyed only in circumstances where convection is prevented or in circumstances where it is forced (when a radiator is fan-assisted, for example).Imagine a situation in which the same two plates are horizontal rather than vertical. In such a case, no convection can occur if the hot plate is above the cold one, and it is not obvious that it occurs in the reverse situation. Whether it does so or not depends on the magnitude of the temperature difference through a dimensionless combination of some of the relevant parameters, ρgαD3(T1 - T2)/ηκ, which is known as the Rayleigh number. If the Rayleigh number is less than 1,708, the fluid is stable—or perhaps it would be more accurate to say that it is metastable—even though it is warmer at the bottom than at the top. However, when 1,708 is exceeded, a pattern of convective rolls known as Bénard cells is established between the plates. Evidence for the existence of such cells in the convecting atmosphere is sometimes seen in the regular columns of cloud that form over regions where the air is rising. Their periodicity can be astonishingly uniform.
Macroscopic instabilities of a convective nature, of which the formation of Bénard cells provides just one example, are a feature of the oceans as well as of the atmosphere and are frequently associated with gradients of salinity rather than gradients of temperature. A serious discussion of atmospheric and oceanic circulation on the Earth, however, requires a more detailed examination of the dynamics of rotating fluids than is given here.
Additional Reading
A classic text that enshrines all the results of 19th-century fluid dynamics is Horace Lamb, Hydrodynamics, 6th ed. (1932, reissued 1993). This remains useful, but many later books, besides being more up-to-date, provide a better-balanced perspective of the subject and have better illustrations. N. Curle and Hubert J. Davies, Modern Fluid Dynamics: Incompressible Flow, vol. 1 (1968, reissued 2000); and G.K. Batchelor, An Introduction to Fluid Dynamics (1967, reissued 1973), can both be recommended to serious students who are not put off by mathematics. D.J. Tritton, Physical Fluid Dynamics, 2nd ed. (1988), adopts a somewhat different approach and contains interesting material on turbulence and convective instabilities. B.S. Massey, Mechanics of Fluids, 8th ed. (2005), covers practical aspects of the subject, including hydrostatics, from an engineering perspective. The development of the subject as a practical science is traced in Hunter Rouse and Simon Ince, History of Hydraulics (1957, reissued 1980).
- Stanley
- Stanley B. Prusiner
- Stanley Cohen
- Stanley Crouch
- Stanley Cup
- Stanley Cup Table
- Stanley Donen
- Stanley Elkin
- Stanley Fish
- Stanley, Francis Edgar; and Stanley, Freelan O.
- Stanley F. Reed
- Stanley Keith Runcorn
- Stanley Ketchel
- Stanley Kramer
- Stanley Kubrick
- Stanley Kunitz
- Stanley Marcus
- Stanley Matthews
- Stanley Melbourne Bruce Bruce, Viscount
- Stanley Melbourne Bruce, Viscount Bruce
- Stanley Middleton
- Stanley Morison
- Stanley, Sir Henry Morton
- Stanley, Thomas
- Stanley Tigerman