function
mathematics
Introduction
in mathematics, an expression, rule, or law that defines a relationship between one variable (the independent variable) and another variable (the dependent variable). Functions are ubiquitous in mathematics and are essential for formulating physical relationships in the sciences. The modern definition of function was first given in 1837 by the German mathematician Peter Dirichlet (Dirichlet, Peter Gustav Lejeune):
If a variable y is so related to a variable x that whenever a numerical value is assigned to x, there is a rule according to which a unique value of y is determined, then y is said to be a function of the independent variable x.
This relationship is commonly symbolized as y=f(x). In addition to f(x), other abbreviated symbols such as g(x) and P(x) are often used to represent functions of the independent variable x, especially when the nature of the function is unknown or unspecified.
Common functions
Many widely used mathematical formulas are expressions of known functions. For example, the formula for the area of a circle, A=πr2, gives the dependent variable A (the area) as a function of the independent variable r (the radius). Functions involving more than two variables also are common in mathematics, as can be seen in the formula for the area of a triangle, A=bh/2, which defines A as a function of both b (base) and h (height). In these examples, physical constraints force the independent variables to be positive numbers. When the independent variables are also allowed to take on negative values—thus, any real number—the functions are known as real-valued functions.
The formula for the area of a circle is an example of a polynomial function. The general form for such functions is
P(x)=a0+a1x+a2x2+⋯+anxn,
where the coefficients (a0,a1,a2,…,an) are given, x can be any real number, and all the powers of x are counting numbers (1,2,3,…). (When the powers of x can be any real number, the result is known as an algebraic function.) Polynomial functions have been studied since the earliest times because of their versatility—practically any relationship involving real numbers can be closely approximated by a polynomial function. Polynomial functions are characterized by the highest power of the independent variable. Special names are commonly used for such powers from one to five—linear, quadratic, cubic, quartic, and quintic.
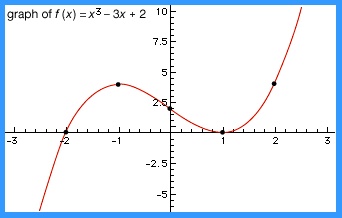 Polynomial functions may be given geometric representation by means of analytic geometry. The independent variable x is plotted along the x-axis (a horizontal line), and the dependent variable y is plotted along the y-axis (a vertical line). The graph of the function then consists of the points with coordinates (x,y) where y=f(x). For example, the graph of the cubic equation f(x)=x3−3x+2 is shown in the figure-->
Polynomial functions may be given geometric representation by means of analytic geometry. The independent variable x is plotted along the x-axis (a horizontal line), and the dependent variable y is plotted along the y-axis (a vertical line). The graph of the function then consists of the points with coordinates (x,y) where y=f(x). For example, the graph of the cubic equation f(x)=x3−3x+2 is shown in the figure--> .
.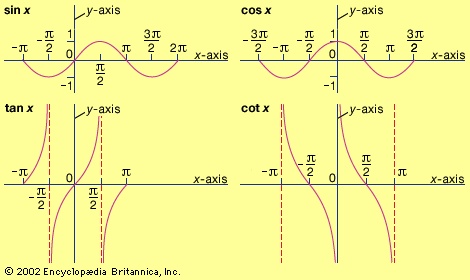 Another common type of function that has been studied since antiquity is the trigonometric functions, such as sinx and cosx, where x is the measure of an angle (see figure-->
Another common type of function that has been studied since antiquity is the trigonometric functions, such as sinx and cosx, where x is the measure of an angle (see figure--> ). Because of their periodic nature, trigonometric functions are often used to model behaviour that repeats, or “cycles.” Nonalgebraic functions, such as exponential (exponential function) and trigonometric functions, are also known as transcendental functions.
). Because of their periodic nature, trigonometric functions are often used to model behaviour that repeats, or “cycles.” Nonalgebraic functions, such as exponential (exponential function) and trigonometric functions, are also known as transcendental functions.Complex functions
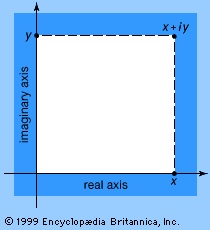 Practical applications of functions whose variables are complex numbers (complex number) are not so easy to illustrate, but they are nevertheless very extensive. They occur, for example, in electrical engineering and aerodynamics. If the complex variable is represented in the form z=x+iy, where i is the imaginary unit (the square root of −1) and x and y are real variables (see figure-->
Practical applications of functions whose variables are complex numbers (complex number) are not so easy to illustrate, but they are nevertheless very extensive. They occur, for example, in electrical engineering and aerodynamics. If the complex variable is represented in the form z=x+iy, where i is the imaginary unit (the square root of −1) and x and y are real variables (see figure--> ), it is possible to split the complex function into real and imaginary parts: f(z)=P(x,y)+iQ(x,y).
), it is possible to split the complex function into real and imaginary parts: f(z)=P(x,y)+iQ(x,y).Inverse functions
By interchanging the roles of the independent and dependent variables in a given function, one can obtain an inverse function. Inverse functions do what their name implies: they undo the action of a function to return a variable to its original state. Thus, if for a given function f(x) there exists a function g(y) such that g(f(x))=x and f(g(y))=y, then g is called the inverse function of f and given the notation f−1, where by convention the variables are interchanged. For example, the function f(x)=2x has the inverse function f−1(x)=x/2.
Other functional expressions
A function may be defined by means of a power series. For example, the infinite series
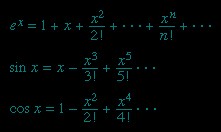
could be used to define these functions for all complex values of x. Other types of series and also infinite products may be used when convenient. An important case is the Fourier series, expressing a function in terms of sines and cosines:
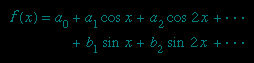
Such representations are of great importance in physics, particularly in the study of wave motion and other oscillatory phenomena.
Sometimes functions are most conveniently defined by means of differential equations (differential equation). For example, y=sinx is the solution of the differential equation d2y/dx2+y=0 having y=0, dy/dx=1 when x=0; y=cosx is the solution of the same equation having y=1, dy/dx=0 when x=0.
- aril
- Ariminum, Council of
- Arinnitti
- Arinos River
- Ariobarzanes
- Arion
- Ariosto, Ludovico
- Arisaema
- Arishima Takeo
- Arishtanemi
- Aristaeus
- Aristagoras
- aristarch
- Aristarchus Of Samos
- Aristarchus Of Samothrace
- Aristeas, Letter of
- Aristide Briand
- Aristide Cavaillé-Coll
- Aristide, Jean-Bertrand
- Aristide Maillol
- Aristides
- Aristides Agramonte y Simoni
- Aristides Quintilianus
- Aristides The Just
- Aristippus