homeomorphism
mathematics
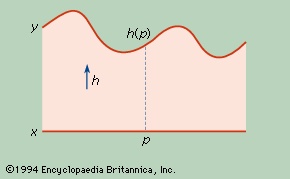 in mathematics, a correspondence between two figures or surfaces or other geometrical objects, defined by a one-to-one mapping that is continuous (continuity) in both directions. The vertical projection shown in the figure-->
in mathematics, a correspondence between two figures or surfaces or other geometrical objects, defined by a one-to-one mapping that is continuous (continuity) in both directions. The vertical projection shown in the figure--> sets up such a one-to-one correspondence between the straight segment x and the curved interval y. If x and y are topologically equivalent, there is a function h:x→y such that h is continuous, h is onto (each point of y corresponds to a point of x), h is one-to-one, and the inverse function, h−1, is continuous. Thus h is called a homeomorphism.
sets up such a one-to-one correspondence between the straight segment x and the curved interval y. If x and y are topologically equivalent, there is a function h:x→y such that h is continuous, h is onto (each point of y corresponds to a point of x), h is one-to-one, and the inverse function, h−1, is continuous. Thus h is called a homeomorphism.A topological property is defined to be a property that is preserved under a homeomorphism. Examples are connectedness, compactness, and, for a plane domain, the number of components of the boundary. The most general type of objects for which homeomorphisms can be defined are topological spaces (topological space). Two spaces are called topologically equivalent if there exists a homeomorphism between them. The properties of size and straightness in Euclidean space are not topological properties, while the connectedness of a figure is. Any simple polygon is homeomorphic to a circle; all figures homeomorphic to a circle are called simple closed curves. These curves have this topological property: they remain connected if one point is removed, but they become disconnected if two points are removed. A figure-eight curve is not homeomorphic to a circle because removing a single point—the crossing point—leaves a disconnected set with two components.
- tincalconite
- Tinctoris, Johannes
- Tindouf
- tineid moth
- tinfoil
- tin-glazed earthenware
- Tingley, Katherine Augusta Westcott
- Tingo María
- Ting, Samuel C.C.
- Tingsten, Herbert Lars Gustaf
- tinguaite
- Tinguely, Jean
- Tinia
- Tinian
- tinikling
- tinkerbird
- Tinkisso River
- tinnitus
- Tinné, Alexandrine-Pieternella-Françoise
- Tino Di Camaino
- Tin Pan Alley
- tinplate
- tin processing
- Tinsukia
- Tintagel