interpolation
mathematics
in mathematics, the determination or estimation of the value of f(x), or a function of x, from certain known values of the function. If x0 \\<…\\< xn and y0=f(x0),…, yn=f(xn) are known, and if x0\\<x\\<xn, then the estimated value of f(x) is said to be an interpolation. If x\\<x0 or x\\>xn, the estimated value of f(x) is said to be an extrapolation.
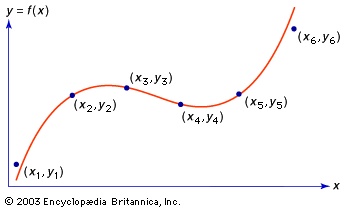If x0, …, xn are given, along with corresponding values y0, …, yn (see the figure-->), interpolation may be regarded as the determination of a function y=f(x) whose graph passes through the n+1 points, (xi, yi) for i = 0, 1, …, n. There are infinitely many such functions, but the simplest is a polynomial interpolation function y=p(x)=a0+a1x+…+anxn with constant ai's such that p(xi)=yi for i=0,…,n. There is exactly one such interpolating polynomial of degree n or less. If the xi's are equally spaced, say by some factor h, then the following formula of Isaac Newton (Newton, Sir Isaac) produces a polynomial function that fits the data: f(x)=a0+a1(x−x0)/h+a2(x−x0)(x−x1)/2!h2+…+an(x−x0)⋯(x−xn−1)/n!hn
Polynomial approximation is useful even if the actual function f(x) is not a polynomial, for the polynomial p(x) often gives good estimates for other values of f(x).
- Caillié, René-Auguste
- Cai Lun
- cai luong
- caiman
- caiman lizard
- Cain
- Caine, Sir Hall
- Caine, Sir Michael
- Cainite
- Cain, James M.
- Caird, Edward
- Caird, John
- Cairene rug
- cairn
- Cairnes, John Elliott
- Cairngorm Mountains
- Cairns
- cairn terrier
- Cairo
- Cairo Conference
- Cairoli, Benedetto
- caisson
- Caitanya
- Caitanya sect
- Caithness