Königsberg bridge problem
mathematics
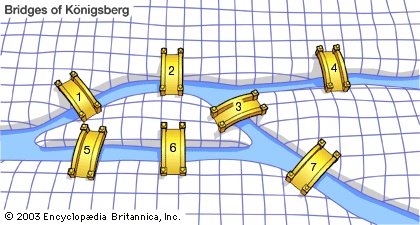 a recreational mathematical puzzle, set in the old Prussian city of Königsberg (now Kaliningrad, Russia), that led to the development of the branches of mathematics known as topology and graph theory. In the early 18th century, the citizens of Königsberg spent their days walking on the intricate arrangement of bridges across the waters of the Pregel (Pregolya) River, which surrounded two central landmasses connected by a bridge (3). Additionally, the first landmass (an island) was connected by two bridges (5 and 6) to the lower bank of the Pregel and also by two bridges (1 and 2) to the upper bank, while the other landmass (which split the Pregel into two branches) was connected to the lower bank by one bridge (7) and to the upper bank by one bridge (4), for a total of seven bridges. According to folklore, the question arose of whether a citizen could take a walk through the town in such a way that each bridge would be crossed exactly once.
a recreational mathematical puzzle, set in the old Prussian city of Königsberg (now Kaliningrad, Russia), that led to the development of the branches of mathematics known as topology and graph theory. In the early 18th century, the citizens of Königsberg spent their days walking on the intricate arrangement of bridges across the waters of the Pregel (Pregolya) River, which surrounded two central landmasses connected by a bridge (3). Additionally, the first landmass (an island) was connected by two bridges (5 and 6) to the lower bank of the Pregel and also by two bridges (1 and 2) to the upper bank, while the other landmass (which split the Pregel into two branches) was connected to the lower bank by one bridge (7) and to the upper bank by one bridge (4), for a total of seven bridges. According to folklore, the question arose of whether a citizen could take a walk through the town in such a way that each bridge would be crossed exactly once.In 1735 the Swiss mathematician Leonhard Euler (Euler, Leonhard) presented a solution to this problem, concluding that such a walk was impossible. To confirm this, suppose that such a walk is possible. In a single encounter with a specific landmass, other than the initial or terminal one, two different bridges must be accounted for: one for entering the landmass and one for leaving it. Thus, each such landmass must serve as an endpoint of a number of bridges equaling twice the number of times it is encountered during the walk. Therefore, each landmass, with the possible exception of the initial and terminal ones if they are not identical, must serve as an endpoint of an even number of bridges. However, for the landmasses of Königsberg, A is an endpoint of five bridges, and B, C, and D are endpoints of three bridges. The walk is therefore impossible.
It would be nearly 150 years before mathematicians would picture the Königsberg bridge problem as a graph consisting of nodes (vertices) representing the landmasses and arcs (edges) representing the bridges. The degree of a vertex of a graph specifies the number of edges incident to it. In modern graph theory, an Eulerian path traverses each edge of a graph once and only once. Thus, Euler's assertion that a graph possessing such a path has at most two vertices of odd degree was the first theorem in graph theory.
Euler described his work as geometria situs—the “geometry of position.” His work on this problem and some of his later work led directly to the fundamental ideas of combinatorial topology, which 19th-century mathematicians referred to as analysis situs—the “analysis of position.” Graph theory and topology, both born in the work of Euler, are now major areas of mathematical research.
- O'Brien, Tim
- O'Brien, William
- O'Brien, William Smith
- Ob River
- O'Bryan, William
- Obscene Publications Act
- obscenity
- Observer, The
- obsessive-compulsive disorder
- obsidian
- obstetrics and gynecology
- Obstfelder, Sigbjørn
- Obuasi
- Obuchi Keizo
- Ob-Ugric languages
- obversion
- Obwalden
- Ocala
- O Canada
- ocarina
- O'Carolan, Turlough
- O'Casey, Sean
- Ocaña
- occasionalism
- Occidental Petroleum Corporation