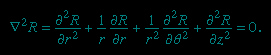second-order partial differential equation widely useful in physics because its solutions R (known as harmonic functions (harmonic function)) occur in problems of electrical, magnetic, and gravitational potentials, of steady-state temperatures, and of hydrodynamics. The equation was discovered by the French mathematician and astronomer Pierre-Simon Laplace (Laplace, Pierre-Simon, marquis de) (1749–1827).

Laplace's equation states that the sum of the second-order partial derivatives (derivative) of R, the unknown function, with respect to the Cartesian coordinates, equals zero:

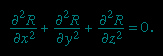
The sum on the left often is represented by the expression ∇²R, in which the symbol ∇² is called the Laplacian, or the Laplace operator.

Many physical systems are more conveniently described by the use of spherical or cylindrical coordinate systems. Laplace's equation can be recast in these coordinates; for example, in cylindrical coordinates, Laplace's equation is