magnetism
physics
Introduction
phenomenon associated with the motion of electric charges (electric charge). This motion can take many forms. It can be an electric current in a conductor or charged particles moving through space, or it can be the motion of an electron in atomic orbit. Magnetism is also associated with elementary particles, such as the electron, that have a property called spin.
Fundamentals
Basic to magnetism are magnetic fields (magnetic field) and their effects on matter, as, for instance, the deflection of moving charges and torques on other magnetic objects. Evidence for the presence of a magnetic field is the magnetic force on charges moving in that field; the force is at right angles to both the field and the velocity of the charge. This force deflects the particles without changing their speed. The deflection can be observed in the electron beam of a television tube when a permanent magnet is brought near the tube. A more familiar example is the torque on a compass needle that acts to align the needle with the magnetic field of the Earth. The needle is a thin piece of iron that has been magnetized—i.e., a small bar magnet. One end of the magnet is called a north pole and the other end a south pole. The force between a north and a south pole is attractive, whereas the force between like poles is repulsive. The magnetic field is sometimes referred to as magnetic induction or magnetic flux density; it is always symbolized by B. Magnetic fields are measured in units of tesla (T). (Another unit of measure commonly used for B is the gauss, though it is no longer considered a standard unit. One gauss equals 10−4 tesla.)
A fundamental property of a magnetic field is that its flux through any closed surface vanishes. (A closed surface is one that completely surrounds a volume.) This is expressed mathematically by div B = 0 and can be understood physically in terms of the field lines representing B. These lines always close on themselves, so that if they enter a certain volume at some point, they must also leave that volume. In this respect, a magnetic field is quite different from an electric field. Electric field lines can begin and end on a charge, but no equivalent magnetic charge has been found in spite of many searches for so-called magnetic monopoles.
The most common source of magnetic fields is the electric current loop. It may be an electric current in a circular conductor or the motion of an orbiting electron in an atom. Associated with both these types of current loops is a magnetic dipole moment, the value of which is iA, the product of the current and the area of the loop. In addition, electrons, protons, and neutrons in atoms have a magnetic dipole moment associated with their intrinsic spin; such magnetic dipole moments represent another important source of magnetic fields. A particle with a magnetic dipole moment is often referred to as a magnetic dipole. (A magnetic dipole may be thought of as a tiny bar magnet. It has the same magnetic field as such a magnet and behaves the same way in external magnetic fields.) When placed in an external magnetic field, a magnetic dipole can be subjected to a torque that tends to align it with the field; if the external field is not uniform, the dipole also can be subjected to a force.
All matter exhibits magnetic properties to some degree. When placed in an inhomogeneous field, matter is either attracted or repelled in the direction of the gradient of the field. This property is described by the magnetic susceptibility of the matter and depends on the degree of magnetization of the matter in the field. Magnetization depends on the size of the dipole moments of the atoms in a substance and the degree to which the dipole moments are aligned with respect to each other. Certain materials, such as iron, exhibit very strong magnetic properties because of the alignment of the magnetic moments of their atoms within certain small regions called domains. Under normal conditions, the various domains have fields that cancel, but they can be aligned with each other to produce extremely large magnetic fields. Various alloys, like NdFeB (an alloy of neodymium, iron, and boron), keep their domains aligned and are used to make permanent magnets. The strong magnetic field produced by a typical three-millimetre-thick magnet of this material is comparable to an electromagnet made of a copper loop carrying a current of several thousand amperes. In comparison, the current in a typical light bulb is 0.5 ampere. Since aligning the domains of a material produces a magnet, disorganizing the orderly alignment destroys the magnetic properties of the material. Thermal agitation that results from heating (heat) a magnet to a high temperature destroys its magnetic properties.
Typical magnetic fieldsMagnetic fields vary widely in strength. Some representative values are given in the Table (Typical magnetic fields).
Magnetic field of steady currents
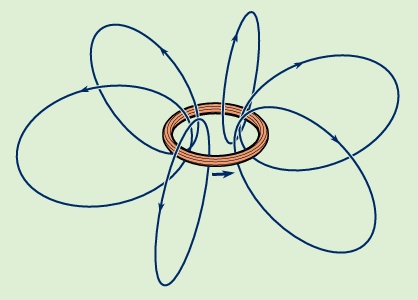 Magnetic fields produced by electric currents can be calculated for any shape of circuit using the law of Biot and Savart (Biot-Savart law), named for the early 19th-century French physicists Jean-Baptiste Biot and Félix Savart. A few magnetic field lines produced by a current in a loop are shown in Figure 1-->
Magnetic fields produced by electric currents can be calculated for any shape of circuit using the law of Biot and Savart (Biot-Savart law), named for the early 19th-century French physicists Jean-Baptiste Biot and Félix Savart. A few magnetic field lines produced by a current in a loop are shown in Figure 1--> . These lines of B form loops around the current. The Biot–Savart law expresses the partial contribution dB from a small segment of conductor to the total B field of a current in the conductor. For a segment of length and orientation dl that carries a current i,
. These lines of B form loops around the current. The Biot–Savart law expresses the partial contribution dB from a small segment of conductor to the total B field of a current in the conductor. For a segment of length and orientation dl that carries a current i, 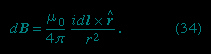
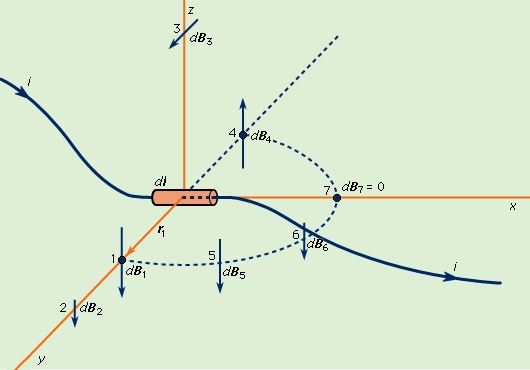 In this equation, μ0 is the permeability (magnetic permeability) of free space and has the value of 4π × 10−7 newton per square ampere. This equation is illustrated in Figure 2-->
In this equation, μ0 is the permeability (magnetic permeability) of free space and has the value of 4π × 10−7 newton per square ampere. This equation is illustrated in Figure 2--> for a small segment of a wire that carries a current so that, at the origin of the coordinate system, the small segment of length dl of the wire lies along the x axis.
for a small segment of a wire that carries a current so that, at the origin of the coordinate system, the small segment of length dl of the wire lies along the x axis.Comparing dB at points 1 and 2 shows the inverse square dependence of the magnitude of the field with distance. The vectors at points 1, 3, and 4, which are all at the same distance from dl, show the direction of dB in a circle around the wire. In position 1, the contribution to the field, dB1, is perpendicular both to the current direction and to the vector r1. Finally, the vectors at 1, 5, 6, and 7 illustrate the angular dependence of the magnitude of dB at a point. The magnitude of dB varies as the sine of the angle between dl and , where is in the direction from dl to the point. It is strongest at 90° to dl and decreases to zero for locations directly in line with dl. The magnetic field of a current in a loop or coil is obtained by summing the individual partial contributions of all the segments of the circuits, taking into account the vector nature of the field. While simple mathematical expressions for the magnetic field can be derived for a few current configurations, most of the practical applications require the use of high-speed computers.
The expression for the magnetic field B a distance r from a long straight wire with current i is

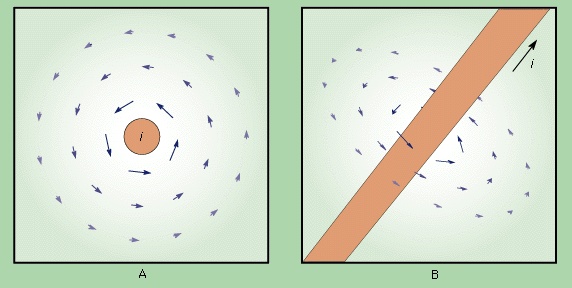
 where θ is a unit vector pointing in a circle around the wire. The B field near a long straight wire with current i can be seen in Figures 2A-->
where θ is a unit vector pointing in a circle around the wire. The B field near a long straight wire with current i can be seen in Figures 2A--> and 2B-->
and 2B--> from the electromagnetism article. The magnetic field at a distance r from a magnetic dipole with moment m is given by
from the electromagnetism article. The magnetic field at a distance r from a magnetic dipole with moment m is given by
Special Comp-->

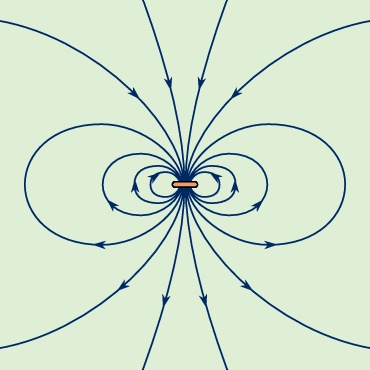 The size of the magnetic dipole moment is m in ampere times square metre (A · m2), and the angle between the direction of m and of r is θ. Both and θ are unit vectors in the direction of r and θ. It is apparent that the magnetic field decreases rapidly as the cube of the distance from the dipole. Equation (36-->
The size of the magnetic dipole moment is m in ampere times square metre (A · m2), and the angle between the direction of m and of r is θ. Both and θ are unit vectors in the direction of r and θ. It is apparent that the magnetic field decreases rapidly as the cube of the distance from the dipole. Equation (36--> ) is also valid for a small current loop with current i, when the distance r is much greater than the size of the current loop. A loop of area A has a magnetic dipole moment with a magnitude m = iA; its direction is perpendicular to the plane of the loop, along the direction of B inside the loop. If the fingers of the right hand are curled and held in the direction of the current in the loop, the extended thumb points in the direction of m. In Figure 1-->
) is also valid for a small current loop with current i, when the distance r is much greater than the size of the current loop. A loop of area A has a magnetic dipole moment with a magnitude m = iA; its direction is perpendicular to the plane of the loop, along the direction of B inside the loop. If the fingers of the right hand are curled and held in the direction of the current in the loop, the extended thumb points in the direction of m. In Figure 1--> , the dipole moment of the current in the loop points up; in Figure 3-->
, the dipole moment of the current in the loop points up; in Figure 3--> , m points down because the current flows in a clockwise direction when viewed from above.
, m points down because the current flows in a clockwise direction when viewed from above.


 The size of the magnetic dipole moment is m in ampere times square metre (A · m2), and the angle between the direction of m and of r is θ. Both and θ are unit vectors in the direction of r and θ. It is apparent that the magnetic field decreases rapidly as the cube of the distance from the dipole. Equation (36-->
The size of the magnetic dipole moment is m in ampere times square metre (A · m2), and the angle between the direction of m and of r is θ. Both and θ are unit vectors in the direction of r and θ. It is apparent that the magnetic field decreases rapidly as the cube of the distance from the dipole. Equation (36--> ) is also valid for a small current loop with current i, when the distance r is much greater than the size of the current loop. A loop of area A has a magnetic dipole moment with a magnitude m = iA; its direction is perpendicular to the plane of the loop, along the direction of B inside the loop. If the fingers of the right hand are curled and held in the direction of the current in the loop, the extended thumb points in the direction of m. In Figure 1-->
) is also valid for a small current loop with current i, when the distance r is much greater than the size of the current loop. A loop of area A has a magnetic dipole moment with a magnitude m = iA; its direction is perpendicular to the plane of the loop, along the direction of B inside the loop. If the fingers of the right hand are curled and held in the direction of the current in the loop, the extended thumb points in the direction of m. In Figure 1--> , the dipole moment of the current in the loop points up; in Figure 3-->
, the dipole moment of the current in the loop points up; in Figure 3--> , m points down because the current flows in a clockwise direction when viewed from above.
, m points down because the current flows in a clockwise direction when viewed from above. The magnetic field of the current loop in Figure 3-->
The magnetic field of the current loop in Figure 3--> at points far from the loop has the same shape as the electric field of an electric dipole; the latter consists of two equal charges of opposite sign separated by a small distance. Magnetic dipoles, like electric dipoles, occur in a variety of situations. Electrons (electron) in atoms have a magnetic dipole moment that corresponds to the current of their orbital motion around the nucleus. In addition, the electrons have a magnetic dipole moment associated with their spin. The Earth's magnetic field is thought to be the result of currents related to the planet's rotation. The magnetic field far from a small bar magnet is well represented by the field of a magnetic dipole. In most of these cases, moving charge produces a magnetic field B. Inside a long solenoid with current i and away from its ends, the magnetic field is uniform and directed along the axis of the solenoid. A solenoid of this kind can be made by wrapping some conducting wire tightly around a long hollow cylinder. The value of the field is
at points far from the loop has the same shape as the electric field of an electric dipole; the latter consists of two equal charges of opposite sign separated by a small distance. Magnetic dipoles, like electric dipoles, occur in a variety of situations. Electrons (electron) in atoms have a magnetic dipole moment that corresponds to the current of their orbital motion around the nucleus. In addition, the electrons have a magnetic dipole moment associated with their spin. The Earth's magnetic field is thought to be the result of currents related to the planet's rotation. The magnetic field far from a small bar magnet is well represented by the field of a magnetic dipole. In most of these cases, moving charge produces a magnetic field B. Inside a long solenoid with current i and away from its ends, the magnetic field is uniform and directed along the axis of the solenoid. A solenoid of this kind can be made by wrapping some conducting wire tightly around a long hollow cylinder. The value of the field is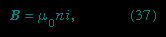
where n is the number of turns per unit length of the solenoid.
Magnetic forces (magnetic force)
Lorentz force
A magnetic field B imparts a force on moving charged particles. The entire electromagnetic force on a charged particle with charge q and velocity v is called the Lorentz force (after the Dutch physicist Hendrik A. Lorentz) and is given by

The first term is contributed by the electric field. The second term is the magnetic force and has a direction perpendicular to both the velocity v and the magnetic field B. The magnetic force is proportional to q and to the magnitude of v × B. In terms of the angle ϕ between v and B, the magnitude of the force equals qvB sin ϕ. An interesting result of the Lorentz force is the motion of a charged particle in a uniform magnetic field. If v is perpendicular to B (i.e., with the angle ϕ between v and B of 90°), the particle will follow a circular trajectory with a radius of r = mv/qB. If the angle ϕ is less than 90°, the particle orbit will be a helix with an axis parallel to the field lines. If ϕ is zero, there will be no magnetic force on the particle, which will continue to move undeflected along the field lines. Charged particle accelerators (particle accelerator) like cyclotrons make use of the fact that particles move in a circular orbit when v and B are at right angles. For each revolution, a carefully timed electric field gives the particles additional kinetic energy, which makes them travel in increasingly larger orbits. When the particles have acquired the desired energy, they are extracted and used in a number of different ways, from fundamental studies of the properties of matter to the medical treatment of cancer.
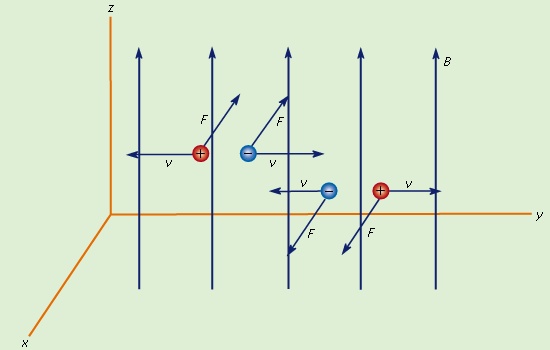
 The magnetic force on a moving charge reveals the sign of the charge carriers in a conductor. A current flowing from right to left in a conductor can be the result of positive charge carriers moving from right to left or negative charges moving from left to right, or some combination of each. When a conductor is placed in a B field perpendicular to the current, the magnetic force on both types of charge carriers is in the same direction. This force, which can be seen in Figure 3-->
The magnetic force on a moving charge reveals the sign of the charge carriers in a conductor. A current flowing from right to left in a conductor can be the result of positive charge carriers moving from right to left or negative charges moving from left to right, or some combination of each. When a conductor is placed in a B field perpendicular to the current, the magnetic force on both types of charge carriers is in the same direction. This force, which can be seen in Figure 3--> from the electromagnetism article, gives rise to a small potential difference between the sides of the conductor. Known as the Hall effect, this phenomenon (discovered by the American physicist Edwin H. Hall) results when an electric field is aligned with the direction of the magnetic force. As is evident in Figure 3-->
from the electromagnetism article, gives rise to a small potential difference between the sides of the conductor. Known as the Hall effect, this phenomenon (discovered by the American physicist Edwin H. Hall) results when an electric field is aligned with the direction of the magnetic force. As is evident in Figure 3--> from the electromagnetism article, the sign of the potential differs according to the sign of the charge carrier because, in one case, positive charges are pushed toward the reader and, in the other, negative charges are pushed in that direction. The Hall effect shows that electrons dominate the conduction of electricity in copper. In zinc, however, conduction is dominated by the motion of positive charge carriers. Electrons in zinc that are excited from the valence band leave holes (hole), which are vacancies (i.e., unfilled levels) that behave like positive charge carriers. The motion of these holes accounts for most of the conduction of electricity in zinc.
from the electromagnetism article, the sign of the potential differs according to the sign of the charge carrier because, in one case, positive charges are pushed toward the reader and, in the other, negative charges are pushed in that direction. The Hall effect shows that electrons dominate the conduction of electricity in copper. In zinc, however, conduction is dominated by the motion of positive charge carriers. Electrons in zinc that are excited from the valence band leave holes (hole), which are vacancies (i.e., unfilled levels) that behave like positive charge carriers. The motion of these holes accounts for most of the conduction of electricity in zinc.If a wire with a current i is placed in an external magnetic field B, how will the force on the wire depend on the orientation of the wire? Since a current represents a movement of charges in the wire, the Lorentz force given in equation (38--> ) acts on the moving charges. Because these charges are bound to the conductor, the magnetic forces on the moving charges are transferred to the wire. The force on a small length dl of the wire depends on the orientation of the wire with respect to the field. The magnitude of the force is given by idlB sin ϕ, where ϕ is the angle between B and dl. There is no force when ϕ = 0 or 180°, both of which correspond to a current along a direction parallel to the field. The force is at a maximum when the current and field are perpendicular to each other. The force is obtained from equation (38-->
) acts on the moving charges. Because these charges are bound to the conductor, the magnetic forces on the moving charges are transferred to the wire. The force on a small length dl of the wire depends on the orientation of the wire with respect to the field. The magnitude of the force is given by idlB sin ϕ, where ϕ is the angle between B and dl. There is no force when ϕ = 0 or 180°, both of which correspond to a current along a direction parallel to the field. The force is at a maximum when the current and field are perpendicular to each other. The force is obtained from equation (38--> ) and is given by
) and is given by
 ) acts on the moving charges. Because these charges are bound to the conductor, the magnetic forces on the moving charges are transferred to the wire. The force on a small length dl of the wire depends on the orientation of the wire with respect to the field. The magnitude of the force is given by idlB sin ϕ, where ϕ is the angle between B and dl. There is no force when ϕ = 0 or 180°, both of which correspond to a current along a direction parallel to the field. The force is at a maximum when the current and field are perpendicular to each other. The force is obtained from equation (38-->
) acts on the moving charges. Because these charges are bound to the conductor, the magnetic forces on the moving charges are transferred to the wire. The force on a small length dl of the wire depends on the orientation of the wire with respect to the field. The magnitude of the force is given by idlB sin ϕ, where ϕ is the angle between B and dl. There is no force when ϕ = 0 or 180°, both of which correspond to a current along a direction parallel to the field. The force is at a maximum when the current and field are perpendicular to each other. The force is obtained from equation (38--> ) and is given by
) and is given by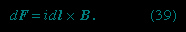
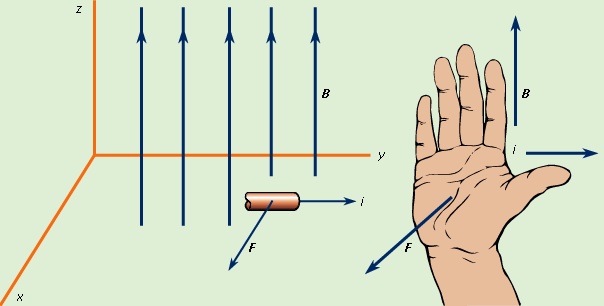 Again, the cross product denotes a direction perpendicular to both dl and B. The direction of dF is given by the right-hand rule illustrated in Figure 4-->
Again, the cross product denotes a direction perpendicular to both dl and B. The direction of dF is given by the right-hand rule illustrated in Figure 4--> . As shown, the fingers are in the direction of B; the current (or in the case of a positive moving point charge, the velocity) is in the direction of the thumb, and the force is perpendicular to the palm.
. As shown, the fingers are in the direction of B; the current (or in the case of a positive moving point charge, the velocity) is in the direction of the thumb, and the force is perpendicular to the palm.Repulsion or attraction between two magnetic dipoles
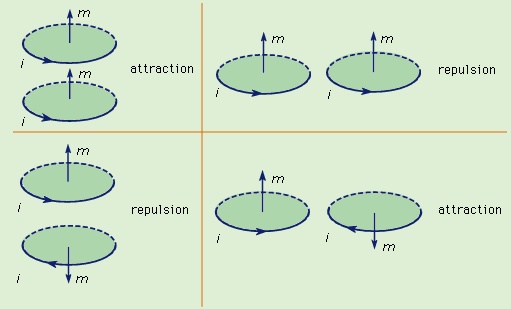





 The force between two wires, each of which carries a current, can be understood from the interaction of one of the currents with the magnetic field produced by the other current. For example, the force between two parallel wires carrying currents in the same direction is attractive. It is repulsive if the currents are in opposite directions. Two circular current loops, located one above the other and with their planes parallel, will attract if the currents are in the same directions and will repel if the currents are in opposite directions. The situation is shown on the left side of Figure 5-->
The force between two wires, each of which carries a current, can be understood from the interaction of one of the currents with the magnetic field produced by the other current. For example, the force between two parallel wires carrying currents in the same direction is attractive. It is repulsive if the currents are in opposite directions. Two circular current loops, located one above the other and with their planes parallel, will attract if the currents are in the same directions and will repel if the currents are in opposite directions. The situation is shown on the left side of Figure 5--> . When the loops are side by side as on the right side of Figure 5-->
. When the loops are side by side as on the right side of Figure 5--> , the situation is reversed. For two currents flowing in the same direction, whether clockwise or counterclockwise, the force is repulsive, while for opposite directions, it is attractive. The nature of the force for the loops depicted in Figure 5-->
, the situation is reversed. For two currents flowing in the same direction, whether clockwise or counterclockwise, the force is repulsive, while for opposite directions, it is attractive. The nature of the force for the loops depicted in Figure 5--> can be obtained by considering the direction of the currents in the parts of the loops that are closest to each other: same current direction, attraction; opposite current direction, repulsion. This seemingly complicated force between current loops can be understood more simply by treating the fields as though they originated from magnetic dipoles. As discussed above, the B field of a small current loop is well represented by the field of a magnetic dipole at distances that are large compared to the size of the loop. In another way of looking at the interaction of current loops, the loops of Figure 5A-->
can be obtained by considering the direction of the currents in the parts of the loops that are closest to each other: same current direction, attraction; opposite current direction, repulsion. This seemingly complicated force between current loops can be understood more simply by treating the fields as though they originated from magnetic dipoles. As discussed above, the B field of a small current loop is well represented by the field of a magnetic dipole at distances that are large compared to the size of the loop. In another way of looking at the interaction of current loops, the loops of Figure 5A--> and 5B-->
and 5B--> are replaced in Figure 6A-->
are replaced in Figure 6A--> and 6B-->
and 6B--> by small permanent magnets, with the direction of the magnets from south to north corresponding to the direction of the magnetic moment of the loop m. Outside the magnets, the magnetic field lines point away from the north pole and toward the south pole.
by small permanent magnets, with the direction of the magnets from south to north corresponding to the direction of the magnetic moment of the loop m. Outside the magnets, the magnetic field lines point away from the north pole and toward the south pole.
 It is easy to understand the nature of the forces in Figures 5-->
It is easy to understand the nature of the forces in Figures 5--> and 6-->
and 6--> with the rule that two north poles repulse each other and two south poles repulse each other, while unlike poles attract. As was noted earlier, Coulomb established an inverse square law of force for magnetic poles and electric charges; according to his law, unlike poles attract and like poles repel, just as unlike charges attract and like charges repel. Today, Coulomb's law refers only to charges, but historically it provided the foundation for a magnetic potential analogous to the electric potential.
with the rule that two north poles repulse each other and two south poles repulse each other, while unlike poles attract. As was noted earlier, Coulomb established an inverse square law of force for magnetic poles and electric charges; according to his law, unlike poles attract and like poles repel, just as unlike charges attract and like charges repel. Today, Coulomb's law refers only to charges, but historically it provided the foundation for a magnetic potential analogous to the electric potential.The alignment of a magnetic compass needle with the direction of an external magnetic field is a good example of the torque to which a magnetic dipole is subjected. The torque has a magnitude τ = mB sin ϑ. Here, ϑ is the angle between m and B. The torque τ tends to align m with B. It has its maximum value when ϑ is 90°, and it is zero when the dipole is in line with the external field. Rotating a magnetic dipole from a position where ϑ = 0 to a position where ϑ = 180° requires work. Thus, the potential energy of the dipole depends on its orientation with respect to the field and is given in units of joules by

Equation (40--> ) represents the basis for an important medical application—namely, magnetic resonance imaging (MRI), also known as nuclear magnetic resonance imaging. MRI involves measuring the concentration of certain atoms, most commonly those of hydrogen, in body tissue and processing this measurement data to produce high-resolution images of organs and other anatomical structures. When hydrogen atoms are placed in a magnetic field, their nuclei (protons) tend to have their magnetic moments preferentially aligned in the direction of the field. The magnetic potential energy of the nuclei is calculated according to equation (40-->
) represents the basis for an important medical application—namely, magnetic resonance imaging (MRI), also known as nuclear magnetic resonance imaging. MRI involves measuring the concentration of certain atoms, most commonly those of hydrogen, in body tissue and processing this measurement data to produce high-resolution images of organs and other anatomical structures. When hydrogen atoms are placed in a magnetic field, their nuclei (protons) tend to have their magnetic moments preferentially aligned in the direction of the field. The magnetic potential energy of the nuclei is calculated according to equation (40--> ) as −mB. Inverting the direction of the dipole moment requires an energy of 2mB, since the potential energy in the new orientation is +mB. A high-frequency oscillator provides energy in the form of electromagnetic radiation of frequency ν, with each quantum of radiation having an energy hν, where h is Planck's constant. The electromagnetic radiation from the oscillator consists of high-frequency radio waves, which are beamed into the patient's body while it is subjected to a strong magnetic (magnetic resonance) field. When the resonance condition hν = 2mB is satisfied, the hydrogen nuclei in the body tissue absorb the energy and reverse their orientation. The resonance condition is met in only a small region of the body at any given time, and measurement of the energy absorption reveals the concentration of hydrogen atoms in that region alone. The magnetic field in an MRI scanner is usually provided by a large solenoid with B of one to three teslas. A number of “gradient coils” insures that the resonance condition is satisfied solely in the limited region inside the solenoid at any particular time; the coils are used to move this small target region, thereby making it possible to scan the patient's body throughout. The frequency of the radiation ν is determined by the value of B and is typically 40 to 130 megahertz. The MRI technique does not harm the patient because the energy of the quanta of the electromagnetic radiation is much smaller than the thermal energy of a molecule in the human body.
) as −mB. Inverting the direction of the dipole moment requires an energy of 2mB, since the potential energy in the new orientation is +mB. A high-frequency oscillator provides energy in the form of electromagnetic radiation of frequency ν, with each quantum of radiation having an energy hν, where h is Planck's constant. The electromagnetic radiation from the oscillator consists of high-frequency radio waves, which are beamed into the patient's body while it is subjected to a strong magnetic (magnetic resonance) field. When the resonance condition hν = 2mB is satisfied, the hydrogen nuclei in the body tissue absorb the energy and reverse their orientation. The resonance condition is met in only a small region of the body at any given time, and measurement of the energy absorption reveals the concentration of hydrogen atoms in that region alone. The magnetic field in an MRI scanner is usually provided by a large solenoid with B of one to three teslas. A number of “gradient coils” insures that the resonance condition is satisfied solely in the limited region inside the solenoid at any particular time; the coils are used to move this small target region, thereby making it possible to scan the patient's body throughout. The frequency of the radiation ν is determined by the value of B and is typically 40 to 130 megahertz. The MRI technique does not harm the patient because the energy of the quanta of the electromagnetic radiation is much smaller than the thermal energy of a molecule in the human body.
 ) represents the basis for an important medical application—namely, magnetic resonance imaging (MRI), also known as nuclear magnetic resonance imaging. MRI involves measuring the concentration of certain atoms, most commonly those of hydrogen, in body tissue and processing this measurement data to produce high-resolution images of organs and other anatomical structures. When hydrogen atoms are placed in a magnetic field, their nuclei (protons) tend to have their magnetic moments preferentially aligned in the direction of the field. The magnetic potential energy of the nuclei is calculated according to equation (40-->
) represents the basis for an important medical application—namely, magnetic resonance imaging (MRI), also known as nuclear magnetic resonance imaging. MRI involves measuring the concentration of certain atoms, most commonly those of hydrogen, in body tissue and processing this measurement data to produce high-resolution images of organs and other anatomical structures. When hydrogen atoms are placed in a magnetic field, their nuclei (protons) tend to have their magnetic moments preferentially aligned in the direction of the field. The magnetic potential energy of the nuclei is calculated according to equation (40--> ) as −mB. Inverting the direction of the dipole moment requires an energy of 2mB, since the potential energy in the new orientation is +mB. A high-frequency oscillator provides energy in the form of electromagnetic radiation of frequency ν, with each quantum of radiation having an energy hν, where h is Planck's constant. The electromagnetic radiation from the oscillator consists of high-frequency radio waves, which are beamed into the patient's body while it is subjected to a strong magnetic (magnetic resonance) field. When the resonance condition hν = 2mB is satisfied, the hydrogen nuclei in the body tissue absorb the energy and reverse their orientation. The resonance condition is met in only a small region of the body at any given time, and measurement of the energy absorption reveals the concentration of hydrogen atoms in that region alone. The magnetic field in an MRI scanner is usually provided by a large solenoid with B of one to three teslas. A number of “gradient coils” insures that the resonance condition is satisfied solely in the limited region inside the solenoid at any particular time; the coils are used to move this small target region, thereby making it possible to scan the patient's body throughout. The frequency of the radiation ν is determined by the value of B and is typically 40 to 130 megahertz. The MRI technique does not harm the patient because the energy of the quanta of the electromagnetic radiation is much smaller than the thermal energy of a molecule in the human body.
) as −mB. Inverting the direction of the dipole moment requires an energy of 2mB, since the potential energy in the new orientation is +mB. A high-frequency oscillator provides energy in the form of electromagnetic radiation of frequency ν, with each quantum of radiation having an energy hν, where h is Planck's constant. The electromagnetic radiation from the oscillator consists of high-frequency radio waves, which are beamed into the patient's body while it is subjected to a strong magnetic (magnetic resonance) field. When the resonance condition hν = 2mB is satisfied, the hydrogen nuclei in the body tissue absorb the energy and reverse their orientation. The resonance condition is met in only a small region of the body at any given time, and measurement of the energy absorption reveals the concentration of hydrogen atoms in that region alone. The magnetic field in an MRI scanner is usually provided by a large solenoid with B of one to three teslas. A number of “gradient coils” insures that the resonance condition is satisfied solely in the limited region inside the solenoid at any particular time; the coils are used to move this small target region, thereby making it possible to scan the patient's body throughout. The frequency of the radiation ν is determined by the value of B and is typically 40 to 130 megahertz. The MRI technique does not harm the patient because the energy of the quanta of the electromagnetic radiation is much smaller than the thermal energy of a molecule in the human body.The direction of the magnetic moment m of a compass needle is from the end marked S for south to the one marked N for north. The lowest energy occurs for ϑ = 0, when m and B are aligned. In a typical situation, the compass needle comes to rest after a few oscillations and points along the B field in the direction called north. It must be concluded from this that the Earth's North Pole is really a magnetic south pole, with the field lines pointing toward that pole, while its South Pole is a magnetic north pole. Put another way, the dipole moment of the Earth currently points north to south. Short-term changes in the Earth's magnetic field are ascribed to electric currents in the ionosphere. There are also longer-term fluctuations in the locations of the poles. The angle between the compass needle and geographic north is called the magnetic declination (see Earth: The magnetic field of the Earth (geomagnetic field)).
Special Comp--> Special Comp-->
Special Comp-->
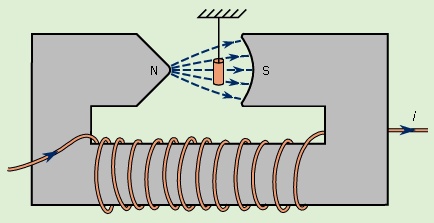 The repulsion or attraction between two magnetic dipoles can be viewed as the interaction of one dipole with the magnetic field produced by the other dipole. The magnetic field is not constant, but varies with the distance from the dipole. When a magnetic dipole with moment m is in a B field that varies with position, it is subjected to a force proportional to that variation—i.e., to the gradient of B. The direction of the force is understood best by considering the potential energy of a dipole in an external B field, as given by equation (40-->
The repulsion or attraction between two magnetic dipoles can be viewed as the interaction of one dipole with the magnetic field produced by the other dipole. The magnetic field is not constant, but varies with the distance from the dipole. When a magnetic dipole with moment m is in a B field that varies with position, it is subjected to a force proportional to that variation—i.e., to the gradient of B. The direction of the force is understood best by considering the potential energy of a dipole in an external B field, as given by equation (40--> ). The force on the dipole is in the direction in which that energy decreases most rapidly. For example, if the magnetic dipole m is aligned with B, then the energy is −mB, and the force is in the direction of increasing B. If m is directed opposite to B, then the potential energy given by equation (40-->
). The force on the dipole is in the direction in which that energy decreases most rapidly. For example, if the magnetic dipole m is aligned with B, then the energy is −mB, and the force is in the direction of increasing B. If m is directed opposite to B, then the potential energy given by equation (40--> ) is +mB, and in this case the force is in the direction of decreasing B. Both types of forces are observed when various samples of matter are placed in a nonuniform magnetic field. Such a field from an electromagnet is sketched in Figure 7-->
) is +mB, and in this case the force is in the direction of decreasing B. Both types of forces are observed when various samples of matter are placed in a nonuniform magnetic field. Such a field from an electromagnet is sketched in Figure 7--> .
.
 Special Comp-->
Special Comp-->
 The repulsion or attraction between two magnetic dipoles can be viewed as the interaction of one dipole with the magnetic field produced by the other dipole. The magnetic field is not constant, but varies with the distance from the dipole. When a magnetic dipole with moment m is in a B field that varies with position, it is subjected to a force proportional to that variation—i.e., to the gradient of B. The direction of the force is understood best by considering the potential energy of a dipole in an external B field, as given by equation (40-->
The repulsion or attraction between two magnetic dipoles can be viewed as the interaction of one dipole with the magnetic field produced by the other dipole. The magnetic field is not constant, but varies with the distance from the dipole. When a magnetic dipole with moment m is in a B field that varies with position, it is subjected to a force proportional to that variation—i.e., to the gradient of B. The direction of the force is understood best by considering the potential energy of a dipole in an external B field, as given by equation (40--> ). The force on the dipole is in the direction in which that energy decreases most rapidly. For example, if the magnetic dipole m is aligned with B, then the energy is −mB, and the force is in the direction of increasing B. If m is directed opposite to B, then the potential energy given by equation (40-->
). The force on the dipole is in the direction in which that energy decreases most rapidly. For example, if the magnetic dipole m is aligned with B, then the energy is −mB, and the force is in the direction of increasing B. If m is directed opposite to B, then the potential energy given by equation (40--> ) is +mB, and in this case the force is in the direction of decreasing B. Both types of forces are observed when various samples of matter are placed in a nonuniform magnetic field. Such a field from an electromagnet is sketched in Figure 7-->
) is +mB, and in this case the force is in the direction of decreasing B. Both types of forces are observed when various samples of matter are placed in a nonuniform magnetic field. Such a field from an electromagnet is sketched in Figure 7--> .
.Magnetization effects in matter
 Regardless of the direction of the magnetic field in Figure 7-->
Regardless of the direction of the magnetic field in Figure 7--> , a sample of copper is magnetically attracted toward the low field region to the right in the drawing. This behaviour is termed diamagnetism. A sample of aluminum, however, is attracted toward the high field region in an effect called paramagnetism. A magnetic dipole moment is induced when matter is subjected to an external field. For copper, the induced dipole moment is opposite to the direction of the external field; for aluminum, it is aligned with that field. The magnetization M of a small volume of matter is the sum (a vector sum) of the magnetic dipole moments in the small volume divided by that volume. M is measured in units of amperes per metre. The degree of induced magnetization is given by the magnetic susceptibility of the material χm, which is commonly defined by the equation
, a sample of copper is magnetically attracted toward the low field region to the right in the drawing. This behaviour is termed diamagnetism. A sample of aluminum, however, is attracted toward the high field region in an effect called paramagnetism. A magnetic dipole moment is induced when matter is subjected to an external field. For copper, the induced dipole moment is opposite to the direction of the external field; for aluminum, it is aligned with that field. The magnetization M of a small volume of matter is the sum (a vector sum) of the magnetic dipole moments in the small volume divided by that volume. M is measured in units of amperes per metre. The degree of induced magnetization is given by the magnetic susceptibility of the material χm, which is commonly defined by the equation
The field H is called the magnetic intensity and, like M, is measured in units of amperes per metre. (It is sometimes also called the magnetic field, but the symbol H is unambiguous.) The definition of H is

Magnetization effects in matter are discussed in some detail below. The permeability (magnetic permeability) μ is often used for ferromagnetic (ferromagnetism) materials such as iron that have a large magnetic susceptibility dependent on the field and the previous magnetic state of the sample; permeability is defined by the equation B = μH. From equations (41--> ) and (42-->
) and (42--> ), it follows that μ = μ0 (1 + χm).
), it follows that μ = μ0 (1 + χm).
 ) and (42-->
) and (42--> ), it follows that μ = μ0 (1 + χm).
), it follows that μ = μ0 (1 + χm).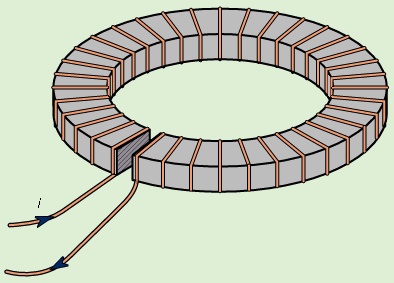

 The effect of ferromagnetic materials in increasing the magnetic field produced by current loops is quite large. Figure 8-->
The effect of ferromagnetic materials in increasing the magnetic field produced by current loops is quite large. Figure 8--> illustrates a toroidal winding of conducting wire around a ring of iron that has a small gap. The magnetic field inside a toroidal winding similar to the one illustrated in Figure 8-->
illustrates a toroidal winding of conducting wire around a ring of iron that has a small gap. The magnetic field inside a toroidal winding similar to the one illustrated in Figure 8--> but without the iron ring is given by B = μ0Ni/2πr, where r is the distance from the axis of the toroid, N is the number of turns, and i is the current in the wire. The value of B for r = 0.1 metre, N = 100, and i = 10 amperes is only 0.002 tesla—about 50 times the magnetic field at the Earth's surface. If the same toroid is wound around an iron ring with no gap, the magnetic field inside the iron is larger by a factor equal to μ/μ0, where μ is the magnetic permeability of the iron. For low-carbon iron in these conditions, μ = 8,000μ0. The magnetic field in the iron is then 1.6 tesla. In a typical electromagnet, iron is used to increase the field in a small region, such as the narrow gap in the iron ring illustrated in Figure 8-->
but without the iron ring is given by B = μ0Ni/2πr, where r is the distance from the axis of the toroid, N is the number of turns, and i is the current in the wire. The value of B for r = 0.1 metre, N = 100, and i = 10 amperes is only 0.002 tesla—about 50 times the magnetic field at the Earth's surface. If the same toroid is wound around an iron ring with no gap, the magnetic field inside the iron is larger by a factor equal to μ/μ0, where μ is the magnetic permeability of the iron. For low-carbon iron in these conditions, μ = 8,000μ0. The magnetic field in the iron is then 1.6 tesla. In a typical electromagnet, iron is used to increase the field in a small region, such as the narrow gap in the iron ring illustrated in Figure 8--> . If the gap is one centimetre wide, the field in that gap is about 0.12 tesla, a 60-fold increase relative to the 0.002-tesla field in the toroid when no iron is used. This factor is typically given by the ratio of the circumference of the toroid to the gap in the ferromagnetic material. The maximum value of B as the gap becomes very small is of course the 1.6 tesla obtained above when there is no gap.
. If the gap is one centimetre wide, the field in that gap is about 0.12 tesla, a 60-fold increase relative to the 0.002-tesla field in the toroid when no iron is used. This factor is typically given by the ratio of the circumference of the toroid to the gap in the ferromagnetic material. The maximum value of B as the gap becomes very small is of course the 1.6 tesla obtained above when there is no gap.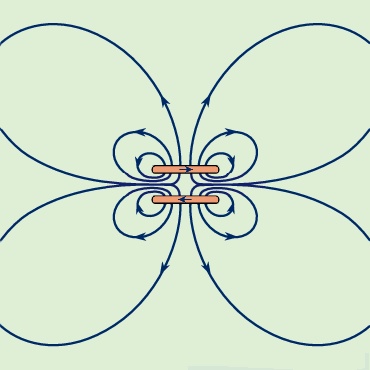 The energy density in a magnetic field is given in the absence of matter by 1/2B2/μ0; it is measured in units of joules per cubic metre. The total magnetic energy can be obtained by integrating the energy density over all space. The direction of the magnetic force can be deduced in many situations by studying distribution of the magnetic field lines; motion is favoured in the direction that tends to decrease the volume of space where the magnetic field is strong. This can be understood because the magnitude of B is squared in the energy density. Figure 9-->
The energy density in a magnetic field is given in the absence of matter by 1/2B2/μ0; it is measured in units of joules per cubic metre. The total magnetic energy can be obtained by integrating the energy density over all space. The direction of the magnetic force can be deduced in many situations by studying distribution of the magnetic field lines; motion is favoured in the direction that tends to decrease the volume of space where the magnetic field is strong. This can be understood because the magnitude of B is squared in the energy density. Figure 9--> shows some lines of the B field for two circular current loops with currents in opposite directions.
shows some lines of the B field for two circular current loops with currents in opposite directions.
 Because Figure 9-->
Because Figure 9--> is a two-dimensional representation of a three-dimensional field, the spacing between the lines reflects the strength of the field only qualitatively. The high values of B between the two loops of the figure show that there is a large energy density in that region and separating the loops would reduce the energy. As discussed above, this is one more way of looking at the source of repulsion between these two loops. Figure 10-->
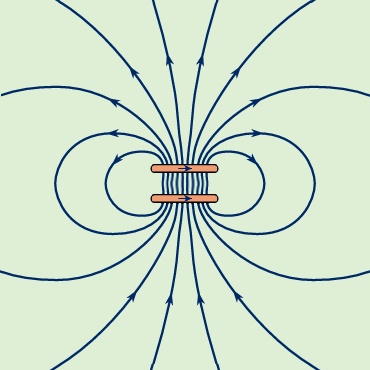
is a two-dimensional representation of a three-dimensional field, the spacing between the lines reflects the strength of the field only qualitatively. The high values of B between the two loops of the figure show that there is a large energy density in that region and separating the loops would reduce the energy. As discussed above, this is one more way of looking at the source of repulsion between these two loops. Figure 10--> shows the B field for two loops with currents in the same direction. The force between the loops is attractive, and the distance separating them is equal to the loop radius. The result is that the B field in the central region between the two loops is homogeneous to a remarkably high degree. Such a configuration is called a Helmholtz coil. By carefully orienting and adjusting the current in a large Helmholtz coil, it is often possible to cancel an external magnetic field (such as the magnetic field of the Earth) in a region of space where experiments require the absence of all external magnetic fields.
shows the B field for two loops with currents in the same direction. The force between the loops is attractive, and the distance separating them is equal to the loop radius. The result is that the B field in the central region between the two loops is homogeneous to a remarkably high degree. Such a configuration is called a Helmholtz coil. By carefully orienting and adjusting the current in a large Helmholtz coil, it is often possible to cancel an external magnetic field (such as the magnetic field of the Earth) in a region of space where experiments require the absence of all external magnetic fields.Magnetic properties of matter
All matter exhibits magnetic properties when placed in an external magnetic field. Even substances (metal) like copper and aluminum that are not normally thought of as having magnetic properties are affected by the presence of a magnetic field such as that produced by either pole of a bar magnet. Depending on whether there is an attraction or repulsion by the pole of a magnet, matter is classified as being either paramagnetic (paramagnetism) or diamagnetic (diamagnetism), respectively. A few materials, notably iron, show a very large attraction toward the pole of a permanent bar magnet; materials of this kind are called ferromagnetic (ferromagnetism).
In 1845 Faraday became the first to classify substances as either diamagnetic or paramagnetic. He based this classification on his observation of the force exerted on substances in an inhomogeneous magnetic field. At moderate field strengths, the magnetization M of a substance is linearly proportional to the strength of the applied field H. The magnetization is specified by the magnetic susceptibility χ (previously labeled χm), defined by the relation M = χH. A sample of volume V placed in a field H directed in the x-direction and increasing in that direction at a rate dH/dx will experience a force in the x-direction of F = χμ0VH (dH/dx). If the magnetic susceptibility χ is positive, the force is in the direction of increasing field strength, whereas if χ is negative, it is in the direction of decreasing field strength. Measurement of the force F in a known field H with a known gradient dH/dx is the basis of a number of accurate methods of determining χ.
Substances for which the magnetic susceptibility is negative (e.g., copper and silver) are classified as diamagnetic. The susceptibility is small, on the order of −10−5 for solids (solid) and liquids and −10−8 for gases. A characteristic feature of diamagnetism is that the magnetic moment per unit mass in a given field is virtually constant for a given substance over a very wide range of temperatures. It changes little between solid, liquid, and gas; the variation in the susceptibility between solid or liquid and gas is almost entirely due to the change in the number of molecules per unit volume. This indicates that the magnetic moment induced in each molecule by a given field is primarily a property characteristic of the molecule.
Substances for which the magnetic susceptibility is positive are classed as paramagnetic. In a few cases (including most metals), the susceptibility is independent of temperature, but in most compounds it is strongly temperature dependent, increasing as the temperature is lowered. Measurements by the French physicist Pierre Curie (Curie, Pierre) in 1895 showed that for many substances the susceptibility is inversely proportional to the absolute temperature T; that is, χ = C/T. This approximate relationship is known as Curie's law and the constant C as the Curie constant. A more accurate equation is obtained in many cases by modifying the above equation to χ = C/(T − θ), where θ is a constant. This equation is called the Curie–Weiss law (after Curie and Pierre-Ernest Weiss (Weiss, Pierre-Ernest), another French physicist). From the form of this last equation, it is clear that at the temperature T = θ, the value of the susceptibility becomes infinite. Below this temperature, the material exhibits spontaneous magnetization—i.e., it becomes ferromagnetic. Its magnetic properties are then very different from those in the paramagnetic or high-temperature phase. In particular, although its magnetic moment can be changed by the application of a magnetic field, the value of the moment attained in a given field is not always the same; it depends on the previous magnetic, thermal, and mechanical treatment of the sample.
Induced and permanent atomic magnetic dipoles
Whether a substance is paramagnetic or diamagnetic is determined primarily by the presence or absence of free magnetic dipole moments (i.e., those free to rotate) in its constituent atoms. When there are no free moments, the magnetization is produced by currents of the electrons in their atomic orbits. The substance is then diamagnetic, with a negative susceptibility independent of both field strength and temperature.
In matter with free magnetic dipole moments, the orientation of the moments is normally random and, as a result, the substance has no net magnetization. When a magnetic field is applied, the dipoles are no longer completely randomly oriented; more dipoles point with the field than against the field. When this results in a net positive magnetization in the direction of the field, the substance has a positive susceptibility and is classified as paramagnetic.
The forces opposing alignment of the dipoles with the external magnetic field are thermal in origin and thus weaker at low temperatures. The excess number of dipoles pointing with the field is determined by (mB/kT), where mB represents the magnetic energy and kT the thermal energy. When the magnetic energy is small compared to the thermal energy, the excess number of dipoles pointing with the field is proportional to the field and inversely proportional to the absolute temperature, corresponding to Curie's law. When the value of (mB/kT) is large enough to align nearly all the dipoles with the field, the magnetization approaches a saturation value.
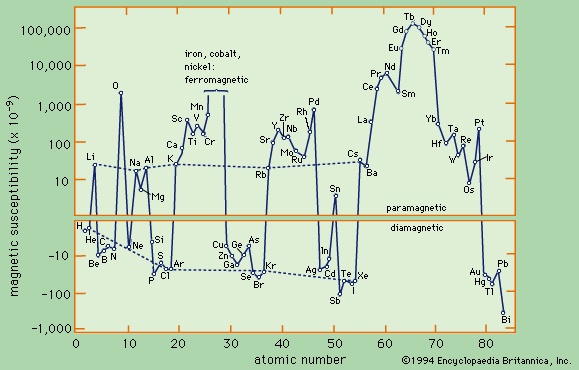 There is a third category of matter in which intrinsic moments are not normally present but appear under the influence of an external magnetic field. The intrinsic moments of conduction electrons in metals behave this way. One finds a small positive susceptibility independent of temperature comparable with the diamagnetic contribution, so that the overall susceptibility of a metal may be positive or negative. The molar susceptibility of elements is shown in Figure 11-->
There is a third category of matter in which intrinsic moments are not normally present but appear under the influence of an external magnetic field. The intrinsic moments of conduction electrons in metals behave this way. One finds a small positive susceptibility independent of temperature comparable with the diamagnetic contribution, so that the overall susceptibility of a metal may be positive or negative. The molar susceptibility of elements is shown in Figure 11--> .
.In addition to the forces exerted on atomic dipoles by an external magnetic field, mutual forces exist between the dipoles. Such forces vary widely for different substances. Below a certain transition temperature depending on the substance, they produce an ordered arrangement of the orientations of the atomic dipoles even in the absence of an external field. The mutual forces tend to align neighbouring dipoles either parallel or antiparallel to one another. Parallel alignment of atomic dipoles throughout large volumes of the substance results in ferromagnetism, with a permanent magnetization on a macroscopic scale. On the other hand, if equal numbers of atomic dipoles are aligned in opposite directions and the dipoles are of the same size, there is no permanent macroscopic magnetization, and this is known as antiferromagnetism. If the atomic dipoles are of different magnitudes and those pointing in one direction are all different in size from those pointing in the opposite direction, there exists permanent magnetization on a macroscopic scale in an effect known as ferrimagnetism. A simple schematic representation of these different possibilities is shown in Figure 12.
In all cases, the material behaves as a paramagnet above the characteristic transition temperature; it acquires a macroscopic magnetic moment only when an external field is applied.
Diamagnetism
When an electron moving in an atomic orbit is in a magnetic field B, the force exerted on the electron produces a small change in the orbital motion; the electron orbit precesses about the direction of B. As a result, each electron acquires an additional angular momentum that contributes to the magnetization of the sample. The susceptibility χ is given by

where Σ \\< r2 \\> is the sum of the mean square radii of all electron orbits in each atom, e and m are the charge and mass of the electron, and N is the number of atoms per unit volume. The negative sign of this susceptibility is a direct consequence of Lenz's law (see above). When B is switched on, the change in motion of each orbit is equivalent to an induced circulating electric current in such a direction that its own magnetic flux opposes the change in magnetic flux through the orbit; i.e., the induced magnetic moment is directed opposite to B.
Since the magnetization M is proportional to the number N of atoms per unit volume, it is sometimes useful to give the susceptibility per mole, χmole. For a kilogram mole (the molecular weight in kilograms), the numerical value of the molar susceptibility is

For an atom, the mean value of Σ \\< r2 \\> is about 10−21 square metre and χmole has values of 10−9 to 10−10; the atomic number Z equals the number of electrons in each atom. The quantity Σ \\< r2 \\> for each atom, and therefore the diamagnetic susceptibility, is essentially independent of temperature. It is also not affected by the surroundings of the atom.
A different kind of diamagnetism occurs in superconductors (superconductivity). The conduction electrons are spread out over the entire metal, and so the induced magnetic moment is governed by the size of the superconducting sample rather than by the size of the individual constituent atoms (a very large effective \\< r2 \\>). The diamagnetism is so strong that the magnetic field is kept out of the superconductor.
Paramagnetism
 Paramagnetism occurs primarily in substances in which some or all of the individual atoms, ions, or molecules possess a permanent magnetic dipole moment. The magnetization of such matter depends on the ratio of the magnetic energy of the individual dipoles to the thermal energy. This dependence can be calculated in quantum theory and is given by the Brillouin function, which depends only on the ratio (B/T). At low magnetic fields, the magnetization is linearly proportional to the field and reaches its maximum saturation value when the magnetic energy is much greater than the thermal energy. Figure 13-->
Paramagnetism occurs primarily in substances in which some or all of the individual atoms, ions, or molecules possess a permanent magnetic dipole moment. The magnetization of such matter depends on the ratio of the magnetic energy of the individual dipoles to the thermal energy. This dependence can be calculated in quantum theory and is given by the Brillouin function, which depends only on the ratio (B/T). At low magnetic fields, the magnetization is linearly proportional to the field and reaches its maximum saturation value when the magnetic energy is much greater than the thermal energy. Figure 13--> shows the dependence of the magnetic moment per ion in units of Bohr magnetons as a function of B/T. (One Bohr magneton equals 9.274 × 10−24 ampere times square metre.)
shows the dependence of the magnetic moment per ion in units of Bohr magnetons as a function of B/T. (One Bohr magneton equals 9.274 × 10−24 ampere times square metre.)In substances that have a nuclear magnetic dipole moment, there is a further contribution to susceptibility. The size of the nuclear magnetic moment is only about one-thousandth that of an atom. Per kilogram mole, χn is on the order of 10−8/T; in solid hydrogen this just exceeds the electronic diamagnetism of 1 K.
Curie's law should hold when mB is much smaller than kT, provided that no other forces act on the atomic dipoles. In many solids, the presence of internal forces may cause the susceptibility to vary in a complicated way. If the forces orient the dipoles parallel to each other, the behaviour is ferromagnetic (see below). The forces may orient the dipoles so that the normal state has no free moment. If the force is sufficiently weak, a small magnetic field can reorient the dipoles, resulting in a net magnetization. This type of paramagnetism occurs for conduction electrons in a metal. In normal metals, each occupied electron state has two electrons with opposite spin orientation. This is a consequence of the Pauli principle of quantum mechanics, which permits no greater occupancy of the energetically favoured states. In the presence of a magnetic field, however, it is energetically more favourable for some of the electrons to move to higher states. With only single electrons in these states, the electron moments can be oriented along the field. The resulting paramagnetic susceptibility is independent of temperature. The net susceptibility is independent of temperature. The net susceptibility of a metal can be of either sign, since the diamagnetic and paramagnetic contributions are of comparable magnitudes.
ferromagnetism
A ferromagnetic substance contains permanent atomic magnetic dipoles that are spontaneously oriented parallel to one another even in the absence of an external field. The magnetic repulsion between two dipoles aligned side by side with their moments in the same direction makes it difficult to understand the phenomenon of ferromagnetism. It is known that within a ferromagnetic material, there is a spontaneous alignment of atoms in large clusters. A new type of interaction, a quantum mechanical effect known as the exchange interaction, is involved. A highly simplified description of how the exchange interaction aligns electrons in ferromagnetic materials is given here.
Role of exchange interaction
The magnetic properties of iron are thought to be the result of the magnetic moment associated with the spin of an electron in an outer atomic shell—specifically, the third d shell. Such electrons are referred to as magnetization electrons. The Pauli exclusion principle prohibits two electrons from having identical properties; for example, no two electrons can be in the same location and have spins in the same direction. This exclusion can be viewed as a “repulsive” mechanism for spins in the same direction; its effect is opposite that required to align the electrons responsible for the magnetization in the iron domains. However, other electrons with spins in the opposite direction, primarily in the fourth s atomic shell, interact at close range with the magnetization electrons, and this interaction is attractive. Because of the attractive effect of their opposite spins, these s-shell electrons influence the magnetization electrons of a number of the iron atoms and align them with each other.
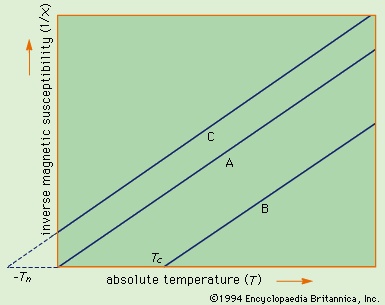 A simple empirical representation of the effect of such exchange forces invokes the idea of an effective internal, or molecular, field Hint, which is proportional in size to the magnetization M; that is, Hint = λM in which λ is an empirical parameter. The resulting magnetization M equals χp(H + λM), in which χp is the susceptibility that the substance would have in the absence of the internal field. Assuming that χp = C/T, corresponding to Curie's law, the equation M = C(H + λM)/T has the solution χ = M/H = C/(T − Cλ) = C/(T − Tc). This result, the Curie–Weiss law, is valid at temperatures greater than the Curie temperature Tc (see below); at such temperatures the substance is still paramagnetic because the magnetization is zero when the field is zero. The internal field, however, makes the susceptibility (magnetic susceptibility) larger than that given by the Curie law. A plot of 1/χ against T still gives a straight line, as shown in Figure 14-->
A simple empirical representation of the effect of such exchange forces invokes the idea of an effective internal, or molecular, field Hint, which is proportional in size to the magnetization M; that is, Hint = λM in which λ is an empirical parameter. The resulting magnetization M equals χp(H + λM), in which χp is the susceptibility that the substance would have in the absence of the internal field. Assuming that χp = C/T, corresponding to Curie's law, the equation M = C(H + λM)/T has the solution χ = M/H = C/(T − Cλ) = C/(T − Tc). This result, the Curie–Weiss law, is valid at temperatures greater than the Curie temperature Tc (see below); at such temperatures the substance is still paramagnetic because the magnetization is zero when the field is zero. The internal field, however, makes the susceptibility (magnetic susceptibility) larger than that given by the Curie law. A plot of 1/χ against T still gives a straight line, as shown in Figure 14--> , but 1/χ becomes zero when the temperature reaches the Curie temperature.
, but 1/χ becomes zero when the temperature reaches the Curie temperature. Curie temperatures for some ferromagnetic substancesSince 1/χ = H/M, M at this temperature must be finite even when the magnetic field is zero. Thus, below the Curie temperature, the substance exhibits a spontaneous magnetization M in the absence of an external field, the essential property of a ferromagnet. The Table (Curie temperatures for some ferromagnetic substances) gives Curie temperature values for various ferromagnetic substances.
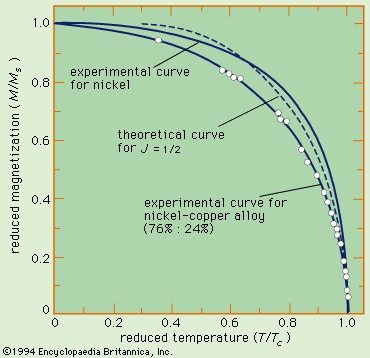 In the ferromagnetic phase below the Curie temperature, the spontaneous alignment is still resisted by random thermal energy, and the spontaneous magnetization M is a function of temperature. The magnitude of M can be found from the paramagnetic equation for the reduced magnetization M/Ms = f(mB/kT) by replacing B with μ(H + λM). This gives an equation that can be solved numerically if the function f is known. When H equals zero, the curve of (M/Ms) should be a unique function of the ratio (T/Tc) for all substances that have the same function f. Such a curve is shown in Figure 15-->
In the ferromagnetic phase below the Curie temperature, the spontaneous alignment is still resisted by random thermal energy, and the spontaneous magnetization M is a function of temperature. The magnitude of M can be found from the paramagnetic equation for the reduced magnetization M/Ms = f(mB/kT) by replacing B with μ(H + λM). This gives an equation that can be solved numerically if the function f is known. When H equals zero, the curve of (M/Ms) should be a unique function of the ratio (T/Tc) for all substances that have the same function f. Such a curve is shown in Figure 15--> , together with experimental results for nickel and a nickel–copper alloy.
, together with experimental results for nickel and a nickel–copper alloy.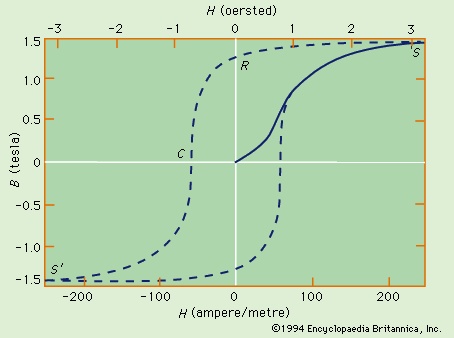 The molecular field theory explains the existence of a ferromagnetic phase and the presence of spontaneous magnetization below the Curie temperature. The dependence of the magnetization on the external field is, however, more complex than the Curie–Weiss theory predicts. The magnetization curve is shown in Figure 16-->
The molecular field theory explains the existence of a ferromagnetic phase and the presence of spontaneous magnetization below the Curie temperature. The dependence of the magnetization on the external field is, however, more complex than the Curie–Weiss theory predicts. The magnetization curve is shown in Figure 16--> for iron, with the field B in the iron plotted against the external field H. The variation is nonlinear, and B reaches its saturation value S in small fields. The relative permeability B/μ0H attains values of 103 to 104 in contrast to an ordinary paramagnet, for which μ is about 1.001 at room temperature. On reducing the external field H, the field B does not return along the magnetization curve. Even at H = 0, its value is not far below the saturation value.
for iron, with the field B in the iron plotted against the external field H. The variation is nonlinear, and B reaches its saturation value S in small fields. The relative permeability B/μ0H attains values of 103 to 104 in contrast to an ordinary paramagnet, for which μ is about 1.001 at room temperature. On reducing the external field H, the field B does not return along the magnetization curve. Even at H = 0, its value is not far below the saturation value.Remanence
When H = 0 (labeled R in the figure), the magnetic field constitutes what is termed the residual flux density, and the retention of magnetization in zero field is called remanence. When the external field is reversed, the value of B falls and passes through zero (point C) at a field strength known as the coercive force. Further increase in the reverse field H sets up a reverse field B that again quickly reaches a saturation value S′. Finally, as the reverse field is removed and a positive field applied, B traces out the lower broken line back to a positive saturation value. Further cycles of H retrace the broken curve, which is known as the hysteresis curve, because the change in B always lags behind the change in H. The hysteresis curve is not unique unless saturation is attained in each direction; interruption and reversal of the cycle at an intermediate field strength results in a hysteresis curve of smaller size.
To explain ferromagnetic phenomena, Weiss (Weiss, Pierre-Ernest) suggested that a ferromagnetic substance contains many small regions (called domains), in each of which the substance is magnetized locally to saturations in some direction. In the unmagnetized state, such directions are distributed at random or in such a way that the net magnetization of the whole sample is zero. Application of an external field changes the direction of magnetization of part or all of the domains, setting up a net magnetization parallel to the field. In a paramagnetic substance, atomic dipoles are oriented on a microscopic scale. In contrast, the magnetization of a ferromagnetic substance involves the reorientation of the magnetization of the domains on a macroscopic scale; large changes occur in the net magnetization even when very small fields are applied. Such macroscopic changes are not immediately reversed when the size of the field is reduced or when its direction is changed. This accounts for the presence of hysteresis and for the finite remanent magnetization.
The technological applications of ferromagnetic substances are extensive, and the size and shape of the hysteresis curve are of great importance. A good permanent magnet must have a large spontaneous magnetization in zero field (i.e., a high retentivity) and a high coercive force to prevent its being easily demagnetized by an external field. Both of these imply a “fat,” almost rectangular hysteresis loop, typical of a hard magnetic material. On the other hand, ferromagnetic substances subjected to alternating fields, as in a transformer, must have a “thin” hysteresis loop because of an energy loss per cycle that is determined by the area enclosed by the hysteresis loop. Such substances are easily magnetized and demagnetized and are known as soft magnetic materials.
antiferromagnetism
Neel temperature of antiferromagnetic substancesIn substances known asantiferromagnets, the mutual forces between pairs of adjacent atomic dipoles are caused by exchange interactions, but the forces between adjacent atomic dipoles have signs opposite those in ferromagnets. As a result, adjacent dipoles tend to line up antiparallel to each other instead of parallel. At high temperatures the material is paramagnetic, but below a certain characteristic temperature the dipoles are aligned in an ordered and antiparallel manner. The transition temperature Tn is known as the Néel temperature, after the French physicist Louis-Eugène-Félix Néel (Néel, Louis-Eugène-Félix), who proposed this explanation of the magnetic behaviour of such materials in 1936. Values of the Néel temperature for some typical antiferromagnetic substances are given in the Table (Neel temperature of antiferromagnetic substances).
The ordered antiferromagnetic state is naturally more complicated than the ordered ferromagnetic state, since there must be at least two sets of dipoles pointing in opposite directions. With an equal number of dipoles of the same size on each set, there is no net spontaneous magnetization on a macroscopic scale. For this reason, antiferromagnetic substances have few commercial applications. In most insulating chemical compounds, the exchange forces between the magnetic ions are of an antiferromagnetic nature.
ferrimagnetism
Lodestone, or magnetite (Fe3O4), belongs to a class of substances known as ferrites (ferrite). Ferrites and some other classes of magnetic substances discovered more recently possess many of the properties of ferromagnetic materials, including spontaneous magnetization and remanence. Unlike the ferromagnetic metals, they have low electric conductivity, however. In alternating magnetic fields, this greatly reduces the energy loss resulting from eddy currents. Since these losses rise with the frequency of the alternating field, such substances are of much importance in the electronics industry.
A notable property of ferrites and associated materials is that the bulk spontaneous magnetization, even at complete magnetic (magnetic dipole) saturation, does not correspond to the value expected if all the atomic dipoles are aligned parallel to each other. The explanation was put forward in 1948 by Néel, who suggested that the exchange forces responsible for the spontaneous magnetization were basically antiferromagnetic in nature and that in the ordered state they contained two (or more) sublattices spontaneously magnetized in opposite directions. In contrast to the simple antiferromagnetic substances considered above, however, the sizes of the magnetization on the two sublattices are unequal, giving a resultant net magnetization parallel to that of the sublattice with the larger moment. For this phenomenon Néel coined the name ferrimagnetism, and substances that exhibit it are called ferrimagnetic materials.
Additional Reading
Gerrit Verschuur, Hidden Attraction (1993), is a delightful popular account of the history and contemporary uses of magnetism. Edward Purcell, Electricity and Magnetism, 2nd ed. (1985), is a superbly written and illustrated college-level introduction to the basic physics and mathematics of magnetism.
- Otto, Sylke
- Otto V. Kuusinen
- Otto von Bismarck
- Otto von Böhtlingk
- Otto von Gerlach
- Otto von Guericke
- Otto von Kotzebue
- Otto von Pack
- Otto Wagner
- Otto Wallach
- Otto Warburg
- Otto Weddigen
- Otto Weininger
- Otto Yulyevich Shmidt
- ottrelite
- Ottumwa
- Ottweiler porcelain
- Otway, Thomas
- Ouachita Geosyncline
- Ouachita Mountains
- Ouachita orogeny
- Ouachita River
- Ouaddaï
- Ouagadougou
- Ouarzazate