mean-value theorem
mathematics
theorem in mathematical analysis dealing with a type of average useful for approximations and for establishing other theorems, such as the fundamental theorem of calculus (analysis).
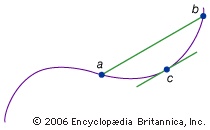The theorem states that the slope of a line connecting any two points on a “smooth” curve is the same as the slope of some line tangent to the curve at a point between the two points. In other words, at some point the slope of the curve must equal its average slope (see figure-->). In symbols, if the function f(x) represents the curve, a and b the two endpoints, and c the point between, then 【f(b)−f(a)】/(b−a)=f′(c), in which f′(c) represents the slope of the tangent line at c, as given by the derivative.Although the mean-value theorem seemed obvious geometrically, proving the result without appeal to diagrams involved a deep examination of the properties of real numbers (real number) and continuous functions (continuity). Other mean-value theorems can be obtained from this basic one by letting f(x) be some special function.
- Jan Žižka, Count (Hrabě)
- Japan
- Japan Airlines
- Japan Communist Party
- Japanese Alps
- Japanese baseball leagues
- Japanese beetle
- Japanese cedar
- Japanese Civil Code
- Japanese deer
- Japanese language
- Japanese law
- Japanese literature
- Japanese mythology
- Japanese Orthodox church
- Japanese philosophy
- Japanese Red Army
- Japanese spaniel
- Japanese torreya
- Japanese yew
- Japan, flag of
- Japanism
- japanning
- Japan Railways Group
- Japan, Sea of