nuclear process permitting the resonance absorption of gamma rays (gamma ray). It is made possible by fixing atomic nuclei in the lattice of solids so that energy is not lost in recoil during the emission and absorption of radiation. The process, discovered by the German-born physicist Rudolf L. Mössbauer (Mössbauer, Rudolf Ludwig) in 1957, constitutes a useful tool for studying diverse scientific phenomena.

In order to understand the basis of the Mössbauer effect, it is necessary to understand several fundamental principles. The first of these is the Doppler shift (Doppler effect). When a locomotive whistles, the frequency, or pitch, of the sound waves is increased while the whistle is approaching a listener and decreased as the whistle recedes. The Doppler formula expresses this change, or shift in frequency, of the waves as a linear function of the velocity of the locomotive. Similarly, when the nucleus of an atom radiates electromagnetic energy in the form of a wave packet known as a gamma-ray photon it is also subject to the Doppler shift. The frequency change, which is perceived as an energy change, depends on how fast the nucleus is moving with respect to the observer.

The second concept, that of nuclear recoil, may be illustrated by the behaviour of a rifle. If it is held loosely during firing, its recoil, or “kick,” will be violent. If it is firmly held against the marksman's shoulder, the recoil will be greatly reduced. The difference in the two situations results from the fact that momentum (the product of mass and velocity) is conserved: the momentum of the system that fires a projectile must be opposite and equal to that of the projectile. By supporting the rifle firmly, the marksman includes his body, with its much greater mass, as part of the firing system and the backward velocity of the system is correspondingly reduced. An atomic nucleus is subject to the same law. When radiation is emitted in the form of a gamma ray, the atom with its nucleus experiences a recoil due to the momentum of the gamma ray. A similar recoil occurs during absorption of radiation by a nucleus.

Finally, it is necessary to understand the principles governing the absorption of gamma rays by nuclei. Nuclei can exist only in certain definite energy states. For a gamma ray to be absorbed its energy must be exactly equal to the difference between two of these states. Such an absorption is called resonance absorption. A gamma ray that is ejected from a nucleus in a free atom cannot be resonantly absorbed by a similar nucleus in another atom because its energy is less than the resonance energy by an amount equal to the kinetic energy given to the recoiling source nucleus.

By embedding the same kind of nuclei in two solids, those in one solid being in a radiating or excited state and those in the other being in an absorbing or ground state, it is possible to use gamma radiation from the first solid for resonant absorption in the second. The method is so sensitive that if one solid moves relative to the other with a velocity as small as a 10th of a centimetre per second the resonance is destroyed by the Doppler shift in the gamma-ray energy. In this fact lies the usefulness of the Mössbauer effect as a tool of experimental physics. If an energy state of the radiating or absorbing nucleus is disturbed by any external effect, resonance absorption will also be nullified. Then, by varying the relative velocity of the radiating and absorbing solids until resonant absorption is reestablished, the precise magnitude of the disturbing effect can be determined.

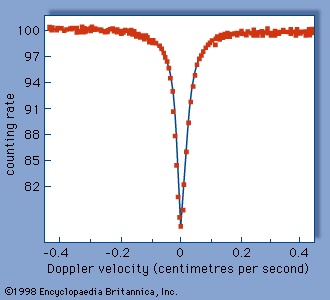
The Mössbauer effect has been observed in more than 35 isotopes. Suitable isotopes must have a stable or long-lived ground state and a low-lying excited state that decays to an appreciable extent by gamma-ray emission. The condition on the energy of the excited state arises from the need to achieve recoil-free gamma-ray emissions. Only if the free-atom recoil energy is small compared to the characteristic lattice vibration energy will there be a finite probability that momentum conservation is satisfied by the recoil of the crystal as a whole with negligible loss of energy. The resulting gamma ray has the full energy of the nuclear transition and is not broadened by thermal vibrations. It consequently has the exact energy for recoil-free resonant reabsorption by a nucleus in its ground state. The condition on the magnitude of the free-atom recoil energy generally restricts the Mössbauer effect to gamma rays with energy less than 150 KeV. The natural width of a resonance or nuclear level, Γ, is related to its lifetime, τ, by Γτ = h/2π, in which h is Planck's constant. The lifetime of the excited state must be greater than 10⁻¹¹ second; otherwise the resonance level would be so broad that the distinction between ordinary and recoil-free emission is lost. The longest useful lifetime is about 10⁻⁵ sec because the corresponding width is comparable to that due to other mechanisms.

Mössbauer's discovery has had far-reaching consequences because it has made available electromagnetic radiation (gamma rays) whose frequency is more precisely defined than any other known to date and has provided a new technique for measuring the interaction of nuclei with their environment. Energy resolution better than one part in 10¹² has been achieved with recoil-free gamma rays.

The Mössbauer effect has found application in many areas of science. In relativity studies the high precision with which the energy of the gamma ray can be measured has made possible a direct demonstration of the gravitational red-shift; i.e., the change in the energy of a quantum of electromagnetic radiation as it moves through a gravitational field. This was accomplished by measuring the Doppler shift required to compensate for the change in the energy of the gamma ray resulting from a change in vertical position of 2,260 centimetres through the Earth's gravitational field. The measured change amounted to 2.5 parts in 10¹⁵ (a Doppler velocity of 2.7 millimetres per hour) and was in close agreement with theoretical predictions. That is, it was found that a photon of energy E behaves as though it had a mass of E/c², in which c is the velocity of light. In a related experiment it was found that the energy of the recoil-free gamma ray decreases with increasing source temperature. This thermal red-shift can be interpreted in a number of ways. It may be viewed as a second-order relativistic Doppler effect resulting from the mean square velocity of the atoms in the solid; i.e., the thermal motion. On the other hand, it can be viewed as a direct demonstration of the relativistic time dilation; i.e., the slowing down of the clock in a moving coordinate system, here the atom, when viewed by a stationary observer. It has been argued that the Mössbauer effect thermal red-shift provides direct experimental resolution of the famous twin paradox of relativity by showing that a space traveler will be younger upon return to Earth than his stay-at-home twin.

Applications in nuclear physics are manifold. The Mössbauer effect makes possible the direct measurement of a gamma-ray line width, which corresponds to the width of the decaying nuclear level. Results are in close agreement with the measured decay time, indicating that the width of recoil-free gamma rays in fact is determined entirely by the lifetime of the decaying state. The isomer shift, the change in the energy of a nuclear gamma ray due to the electrostatic interaction between nuclear and electronic charge, provides a measurement of the change in the nuclear-charge radius when the nucleus is raised to an excited state. The splitting of nuclear levels into hyperfine components (hyperfine structure) by electric field gradients in crystals of low symmetry or by magnetic fields in ferromagnets makes possible the measurement of nuclear electric quadrupole and magnetic dipole moments. Both isomer shifts and hyperfine structure splittings are readily resolved in Mössbauer spectra. The energy width of a Mössbauer resonance provides a direct measurement of the width of the excited state involved in the gamma-ray emission and absorption process. From the width, the lifetime of the excited state can be directly obtained.

Applications in solid-state physics fall broadly into the categories of lattice dynamics and hyperfine interactions, although contributions have been made in other areas. The probability that a gamma-ray emission process will be recoil free depends on the amplitude of the thermal vibrations compared to the wavelength of the gamma ray. A measurement of the fraction of emission events that are recoil free as determined by their ability to be resonantly absorbed provides the mean square amplitude of the thermal motion in the solid. Using single crystals, the amplitude of the motion can be measured in specific crystallographic directions, providing a stringent test of lattice dynamical models. The thermal red-shift mentioned above gives in addition the mean square thermal velocity.

Magnetic hyperfine interactions have been particularly useful in the study of magnetically ordered materials; i.e., ferromagnets, ferrimagnets, and antiferromagnets. The hyperfine interaction gives an indirect measure of the magnetization of the lattice of magnetic ions and has been used to elucidate the details of magnetic interactions as well as their temperature dependence.

Applications in chemistry are based largely on the isomer shift and quadrupole splitting. The former measures the s-electron charge density at the nucleus and gives information on the character of chemical bonds; e.g., valence and covalence. The latter is sensitive both to the symmetry of the structural environment and to the wave function of the outer electrons of the atom containing the Mössbauer nucleus. The technique has been applied to the study of metal-organic compounds of tin and iron, including hemoproteins; to inorganic compounds of iron, tin, iodine, and the rare earths; as well as to clathrates, catalysts, and glasses containing dilute Mössbauer isotopes.