信息论(卷名:数学)
information theory
关于信息加工、存储与分析的理论。按B.麦克米伦和D.斯列皮恩的分类,信息论可分为狭义信息论、一般信息论与广义信息论。狭义信息论主要研究信息量与通信编码问题,关于信息量的引进与通信编码的可行性问题为仙农信息论,而编码的构造算法及它们在计算机上的实现问题称编码理论,因为它大量应用代数理论,又称代数码理论。一般信息论除研究上述编码理论外,还研究信号在噪声中的预测、滤波、检测及调制等问题,又称这些问题为维纳信息论。广义信息论涉及信息处理的有关问题,如计算机科学、经济、社会、心理、生物中的信息处理问题都属于这个范围,也包括关于“信息”等概念的哲学问题,因此它是多学科的综合性科学,又称信息科学。
信息论与数学关系很密切,它不仅深刻地应用了数学的许多分支,而且它的一些分支也是数学的分支。
信息与信息量 信息的一般概念是个哲学概念,它的定义甚多,但还没有一个是得到公认的。日本的《现代用语基础知识》一书中称信息是“生活主体与外部客体之间有关情况的消息”。在人类社会中,语言、文字、书刊报章、广告信件都是信息的表达形式,人与机器、机器与机器、人与生物、生物之间都有各种信息的交换。因此它是物质运动的一种特征形式,反映了各种运动的相互联系。
信息定量化是信息科学的基础。由于信息概念的普遍性与复杂性,信息的定量化过程是一个不断深化的过程,人们不可能通过一种或几种量的定义就可完成这个过程。对已有的各种不同的信息量只有通过它们产生的条件与它们的作用和性质来理解它们的本质。随着信息科学的不断发展,信息量的内容也日趋丰富。
仙农熵是人们首次进行信息定量化的成功尝试,因此人们把仙农信息论看作信息科学发展的开端。
仙农熵反映了一个随机试验(或随机变量)的不肯定性。一个随机试验可用
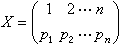 表示,其中1,2,…,n为可能发生的结果,pi为i发生的概率。x的不肯定性大小取决于n的大小与pi分布的均匀程度。这个不肯定性是(p1,p2,…,pn)的一个函数,记为H,它具有性质:(1)对称连续性,即H(p1,p2,…,pn)是p1,p2,…,pn的对称连续函数;(2)H(0,1)=0;(3)如q=pn+pn+1则
表示,其中1,2,…,n为可能发生的结果,pi为i发生的概率。x的不肯定性大小取决于n的大小与pi分布的均匀程度。这个不肯定性是(p1,p2,…,pn)的一个函数,记为H,它具有性质:(1)对称连续性,即H(p1,p2,…,pn)是p1,p2,…,pn的对称连续函数;(2)H(0,1)=0;(3)如q=pn+pn+1则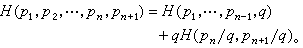 通过一定的数学推导,可得
通过一定的数学推导,可得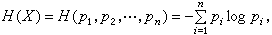 式中 log可分别取2、e、10为底,在工程中相应的H(x)的单位分别为比特(bit)、奈特(nat)、迪西特(decit)。H(x)的形式与热力学中的熵十分相似,因此称H(x)为x的仙农熵。
式中 log可分别取2、e、10为底,在工程中相应的H(x)的单位分别为比特(bit)、奈特(nat)、迪西特(decit)。H(x)的形式与热力学中的熵十分相似,因此称H(x)为x的仙农熵。如(x,Y)为二元随机变量,取值为(x,y),x=1,2…,m,y=1,2,…,n;联合概率分布为pij,则(x,Y)的仙农熵(又称联合熵)为
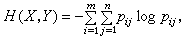 称H(Y|x)=H(x,Y)-H(x)(或H(x|Y)=H(x,Y)-H(Y))为Y关于x(或x关于Y)的条件熵,它表示条件不肯定性,称I(x;Y)=H(x)+H(Y)-H(x,Y)为x、Y的交互信息,它反映了x、Y的相互依赖程度。由仙农熵还可引出其他一系列有关信息量的定义,它们在通信编码中起着重要的作用。
称H(Y|x)=H(x,Y)-H(x)(或H(x|Y)=H(x,Y)-H(Y))为Y关于x(或x关于Y)的条件熵,它表示条件不肯定性,称I(x;Y)=H(x)+H(Y)-H(x,Y)为x、Y的交互信息,它反映了x、Y的相互依赖程度。由仙农熵还可引出其他一系列有关信息量的定义,它们在通信编码中起着重要的作用。信息定量化的一个重要发展是算法信息论的产生,它以计算复杂性作为事物信息的度量标准,它与仙农熵有许多本质上的不同。该理论把信息科学与计算机科学汇成一体,是信息科学的一个重大进展。
通信系统 通信系统由以下要素构成。
信源 即消息的来源,由一个消息符号表H与H上的一个概率分布p(x)表示,H表示消息可能使用的符号的全体,p(x)为符号x(x∈H)可能出现的概率,信源可用[H,p(x)]表示。记x为消息随机变量,它在H上取值,且概率分布为p(x)。
信道 由输入(拍发)信号集合U、输出(接收)信号集合炘与转移概率分布矩阵p(v|u)构成,其中u、v分别是U、V的元素,p(v|u)为拍发u条件下接收为v的概率,
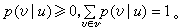 故信道可记为[U,p(v|u),V]。
故信道可记为[U,p(v|u),V]。如U=V=F2(F2为二元域),且p(1|0)=p(0|1)=p,p(0|0)= p(1|1)=1-p,则称这个信道为二元对称信道,如图1
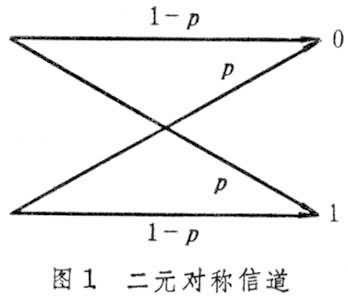 所示。
所示。信源序列与信道序列 在实际通信中,消息与信号是由一串符号向量构成的,消息为:
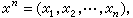 xj∈H,输入信号为
xj∈H,输入信号为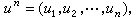 uj∈U,输出信号为
uj∈U,输出信号为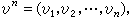 vi∈V;相应的概率分布与转移概率为p(xn),p(vn|un),称[Hn,p(xn)](n=1,2,…)为信源序列,其中 Hn为全体 xn的集合,而称 [Un,p(vn|un),Vn](n=1,2,…)为信道序列。如对任何xn=(x1,x2,…,xn)有
vi∈V;相应的概率分布与转移概率为p(xn),p(vn|un),称[Hn,p(xn)](n=1,2,…)为信源序列,其中 Hn为全体 xn的集合,而称 [Un,p(vn|un),Vn](n=1,2,…)为信道序列。如对任何xn=(x1,x2,…,xn)有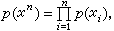 则称信源序列是无记忆的,且由[H,p(x)]决定。否则称为有记忆的。如对任何un=(u1,u2,…,un)、vn=(v1,v2,…,vn)有
则称信源序列是无记忆的,且由[H,p(x)]决定。否则称为有记忆的。如对任何un=(u1,u2,…,un)、vn=(v1,v2,…,vn)有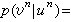
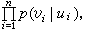 则信道序列是无记忆的且由[U,p(v|u),V]决定。
则信道序列是无记忆的且由[U,p(v|u),V]决定。编码 (encoding) 把信源消息变为信道输入信号的运算称为编码。在工程中由一系列调制所构成,在数学中可看作一个函数ƒn:Hn→Un。
译码 把信道的接收信号还原成信源消息的运算称为译码。在工程中由一系列解调设备构成,在数学中为函数gn:Vn→彑n其中彑n为Hn的复制消息。
又称(ƒn,gn)为编码(coding)。
以上各因素构成通信系统的框图,如图2
 所示。
所示。如信源[Hn,p(xn)]、信道 [Un,p(v|u),Vn]、编码(ƒn,gn)给定,则信源消息xn、输入信号Un、输出信号Vn、复制信号憫n的联合分布确定为
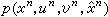
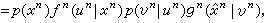 式中ƒn(un|xn)当un=ƒn(xn)时为1,其他情形为0;
式中ƒn(un|xn)当un=ƒn(xn)时为1,其他情形为0; 时为1,其他情形为0。如
时为1,其他情形为0。如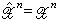 ,则称
,则称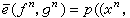
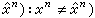 为通信系统的概率误差,其中p(xn,憫n)为由p(xn,un,vn,憫n)决定的边际概率分布。
为通信系统的概率误差,其中p(xn,憫n)为由p(xn,un,vn,憫n)决定的边际概率分布。通信系统的编码问题 对固定的信源与信道,如存在适当的编码(ƒn,gn),使
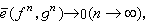 则称这个信源系列在信道序列上是可通过的。仙农信息论的基本问题就是讨论信源在信道上可通过的条件。这个问题又称为编码的存在性(或可行性)问题。为讨论通信系统的编码问题,需讨论信源与信道的结构特征。
则称这个信源系列在信道序列上是可通过的。仙农信息论的基本问题就是讨论信源在信道上可通过的条件。这个问题又称为编码的存在性(或可行性)问题。为讨论通信系统的编码问题,需讨论信源与信道的结构特征。无噪声信源编码问题 信源的编码分等长与不等长两大类型的问题,前者又称为信源的分组编码问题。以下记
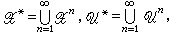 且取U= F2。
且取U= F2。①信源不等长编码问题 如[H,p(x)]为一个信源,称变换ƒ:H→U*为一个不等长编码。这时,对任何xn∈Hn,定义
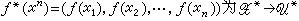 的变换。如ƒ为1-1变换,称ƒ为1-1码;如ƒ*为1-1变换,称ƒ为惟一可译码;如对任何x,x′∈H,ƒ(x)不为ƒ(x′)的前缀,称ƒ为前缀码。记l(ƒ(x))为ƒ(x)向量的长度,则
的变换。如ƒ为1-1变换,称ƒ为1-1码;如ƒ*为1-1变换,称ƒ为惟一可译码;如对任何x,x′∈H,ƒ(x)不为ƒ(x′)的前缀,称ƒ为前缀码。记l(ƒ(x))为ƒ(x)向量的长度,则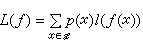 为编码ƒ的平均长度。
为编码ƒ的平均长度。定理1(不等长信源编码定理) a.前缀码必为惟一可译码;惟一可译码是1-1码,但逆命题不一定成立;b.如ƒ是惟一可译码,则L(ƒ)≥H(x );c.存在一个前缀码ƒ,使L(ƒ)≤H(x)+1。由此,这个定理给出了惟一可译码的平均长度与仙农熵之间的关系。
② 分组码的信源编码问题 对信源序列 [ Hn,p(xn)],n=1,2,…,如对任意ε>0,只要 n充分大,就存在一个An嶅Hn,使p(An)>1-ε,且
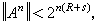 则称R为它的一个可达码率,其中‖A‖为集合A的元素的个数。R-可达码率的概念说明了[Hn,p(xn)]的概率集中在2nR个元素上。
则称R为它的一个可达码率,其中‖A‖为集合A的元素的个数。R-可达码率的概念说明了[Hn,p(xn)]的概率集中在2nR个元素上。定理2(无记忆信源编码定理) 如信源序列[Hn,p(xn)]为由[H,p(x)]决定的无记忆信源,则R=H(x)为最小可达码率。这个定理给出了无记忆信源消息的概率分布集中在2
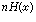 个元上,在工程上称之为信号体积。
个元上,在工程上称之为信号体积。对平稳、遍历的有记忆信源,仙农-麦克米伦-伯雷尼恩定理给出了类似的性质。
信道编码定理 对信道序列
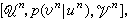 n=1,2,…,如对任意ε>0,只要n 充分大,就存在一列编码
n=1,2,…,如对任意ε>0,只要n 充分大,就存在一列编码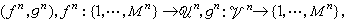 使Mn>2
使Mn>2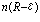 ,且
,且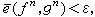 则称R为它的可达码率。这里取
则称R为它的可达码率。这里取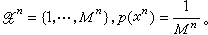 信道序列的最大可达码率称为信道容量,记为C。
信道序列的最大可达码率称为信道容量,记为C。定理3(无记忆信道编码定理) 由[U,p(v|u),V]决定的无记忆信道的信道容量为C=maxI(U;V),其中max对全体U上的概率分布{p(u)}而取,I(U;V)为交互信息。U、V的联合概率分布为p(u,v)= p(v)p(v|u),p(v|u)为无记忆信道转移概率矩阵。可以推出二元对称信道容量为C=1-h(p),其中 h(p)=-plogp-(1-p)log(1-p),这里,p=p(1|0)=p(0|1)。
对有记忆信道也有一系列类似的讨论,定理3的结果可推广到有限记忆信道的情形。
连续信号的通信问题 以上讨论的信息量与编码问题都是离散情形的,也就是消息、信号符号表H、U、V均为有限集合。有时也可取H、U、V为 d 维实数空间R
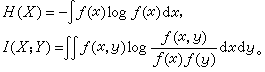 这时有关系式I(x;Y)=H(x)+H(Y)-H(x,Y)。如U=V=R1,且输入输出信号满足关系式V=U+Z,Z是一个与U独立的随机噪声变量,则称这个信道是可加噪声信道;如Z又服从正态分布,则称此信道是可加高斯信道。
这时有关系式I(x;Y)=H(x)+H(Y)-H(x,Y)。如U=V=R1,且输入输出信号满足关系式V=U+Z,Z是一个与U独立的随机噪声变量,则称这个信道是可加噪声信道;如Z又服从正态分布,则称此信道是可加高斯信道。定理4 (可加高斯信道容量公式)对可加高斯信道,如Z服从N (0,σ2)分布,输入信号U的平均功率不超过N,即
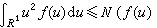 为U 的分布密度),这时信道容量为
为U 的分布密度),这时信道容量为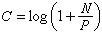 ,其中p=σ2为噪声功率,称
,其中p=σ2为噪声功率,称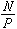 为信噪比。这个公式在工程中是常见的。
为信噪比。这个公式在工程中是常见的。率失真理论 又称具有允许畸变误差下的信源编码理论。在讨论信源编码问题时,考虑了一定程度的概率误差,但没有考虑由于信号的变形而产生的畸变误差,如电视图像中光点的位置与亮度均存在畸变。这些畸变在一定的视觉范围内可以忽略不计,利用这些允许的畸变误差就可以大大减少信号体积。这就是率失真理论的基本点。因此它也是图像、语声等数据压缩处理的理论基础。
在率失真理论中的信源为[H,p(x),
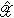 ,d(x,憫)],其中[H,p(x)]的定义如前,
,d(x,憫)],其中[H,p(x)]的定义如前,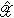 为H的复制信号集合,d(x,憫)为x、憫的误差度量,即x复制为憫的损失。同样定义
为H的复制信号集合,d(x,憫)为x、憫的误差度量,即x复制为憫的损失。同样定义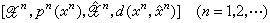 为信源序列。一个信源序列称之为无记忆的,如果[Hn,p(xn)] 是无记忆的,且对任何 xn= (x1, x2, …,xn)、
为信源序列。一个信源序列称之为无记忆的,如果[Hn,p(xn)] 是无记忆的,且对任何 xn= (x1, x2, …,xn)、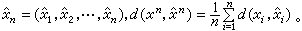
设D是一个允许误差,称R是一个D-可达码率,如果对任意ε>0,只要n充分大,就存在编码(ƒn,gn),ƒn:
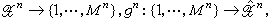 使
使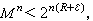 且
且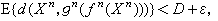 其中E{·}为数学期望,xn的分布为[Hn,p(xn)]。由此R为D-可达的意思是上述信源序列在平均误差不超过D 的条件下信号体积可压缩在2nR范围之内。称最小的D-可达码率为率失真函数,记为R(D)。
其中E{·}为数学期望,xn的分布为[Hn,p(xn)]。由此R为D-可达的意思是上述信源序列在平均误差不超过D 的条件下信号体积可压缩在2nR范围之内。称最小的D-可达码率为率失真函数,记为R(D)。定理5 (无记忆信源的率失真编码定理)如信源序列是无记忆的,则
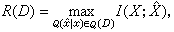 式中Q(D)为转移概率矩阵(Q(憫|x),x∈H,憫∈
式中Q(D)为转移概率矩阵(Q(憫|x),x∈H,憫∈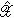 )的集合,
)的集合,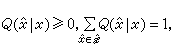 且
且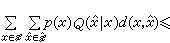 D。而X、憫 的联合分布为p(x,憫)=p(x)Q(憫|x)。
D。而X、憫 的联合分布为p(x,憫)=p(x)Q(憫|x)。如取
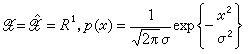 (即信源分布密度为正态分布),且
(即信源分布密度为正态分布),且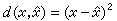 为均方误差,则可导出
为均方误差,则可导出 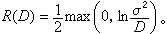 一般有记忆高斯平稳过程,如它的谱密度为
一般有记忆高斯平稳过程,如它的谱密度为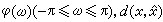 为均方误差,则
为均方误差,则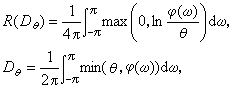 式中θ为参变量。
式中θ为参变量。多用信息论 图2
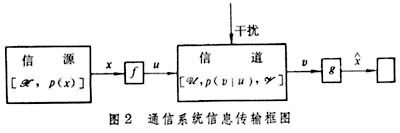 中讨论的通信系统称为简单系统,它的信源、信道输入输出都是单一的。如讨论的信源是多重的或信道的输入输出是多重的,则它们的编码问题都称为多用信息论编码问题。它有下列主要类型。
中讨论的通信系统称为简单系统,它的信源、信道输入输出都是单一的。如讨论的信源是多重的或信道的输入输出是多重的,则它们的编码问题都称为多用信息论编码问题。它有下列主要类型。多重相关信源编码问题 它讨论若干个不相独立的信源编码的压缩长度(信号体积)问题。重要的模型有如斯列皮恩-沃尔夫-科韦模型(图3),
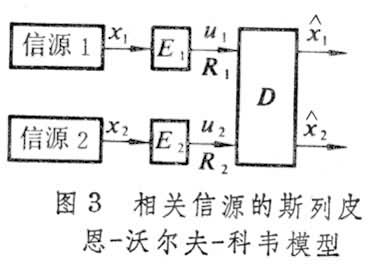
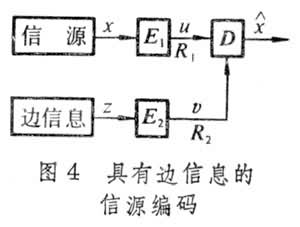
 其中R1、R2分别为信源x1、x2的压缩率,E1、E2为编码器,D为译码器。又如边信息模型(图4),Z为一个与x相关的边信息, E1、E2为编码器、译码器利用边信息的开关,R1、R2为信源与边信息的压缩码率。
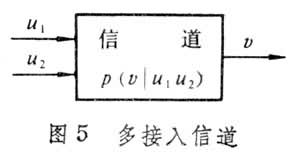
其中R1、R2分别为信源x1、x2的压缩率,E1、E2为编码器,D为译码器。又如边信息模型(图4),Z为一个与x相关的边信息, E1、E2为编码器、译码器利用边信息的开关,R1、R2为信源与边信息的压缩码率。多接入信道编码问题 它的背景是通信卫星模型。多接入信道具有多重输入信号和单重输出信号(图5)。
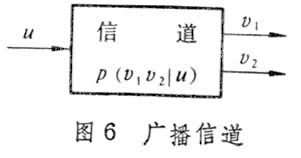
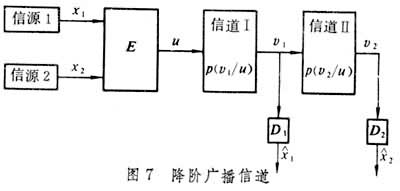
广播信道 模型来自电视卫星。该信道具有单重输入和多重输出,又可分为标准广播信道(图6)与降价(转播)广播信道(图7)。
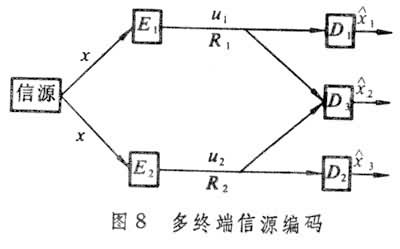
多终端信源编码问题 模型来自兼听系统。几个用户同时收听同一信源,他们分别独立地获取部分信息,关于这些信息的综合分析是多终端问题。如图8所示,这里,用户1、2分别从信源x上获取R1、R2的信息率,用户3可同时利用R1、R2的信息。要讨论的问题是这三个用户的失真度。
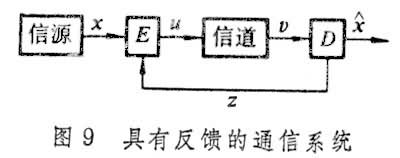
具有反馈信号的编码问题 如图9所示,Z为由终端反馈到编码器的信号,所要讨论的是在有反馈条件下信道容量的提高问题。
代数码 仙农信息论给出了通信系统的可行性,也确立了编码的若干原则,在工程上如何实现上述数据压缩编码与误差纠正编码则是十分复杂的,不仅要构造具体的编译码函数,还要建立在计算机上可实现的算法,因此必须借助于代数工具。
如取输入信号集合U=Fq为q元有限域, 则Un为Fq域上的n维线性空间;如U0为Un的一个k维线性子空间,则称U0为q元的(n,k)线性码。如记g嬫∈Un,i=1,2,…,k为U0的一组基,
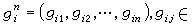 Fq,则称矩阵
Fq,则称矩阵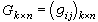 为线性码的生成矩阵。对任何un∈Un,定义d(un)为un的非零元分量数,称为汉明势,且记
为线性码的生成矩阵。对任何un∈Un,定义d(un)为un的非零元分量数,称为汉明势,且记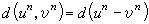 为un、vn的汉明距离,其中un-vn为向量空间Un上的差。这时称
为un、vn的汉明距离,其中un-vn为向量空间Un上的差。这时称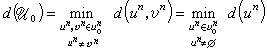 为线性码U0的最小距离,其中═为n维零向量。对任何un∈U0,如
为线性码U0的最小距离,其中═为n维零向量。对任何un∈U0,如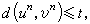 ,则vn唘U0,这时称u0码能检出t个错。对线性码U0,如存在一个使Un→U恄的函数g,且对任何
,则vn唘U0,这时称u0码能检出t个错。对线性码U0,如存在一个使Un→U恄的函数g,且对任何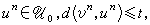 必有g(vn)=un,则称U0能纠正t个错。
必有g(vn)=un,则称U0能纠正t个错。定理6 线性码U0能检出d(U0)-1个错,且能纠正
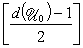 个错。
个错。若U0,U奿为两个线性码,且
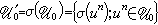 ,则称U0、U奿等价;其中σ为{1,2,…,n}的一个置换,且对任何
,则称U0、U奿等价;其中σ为{1,2,…,n}的一个置换,且对任何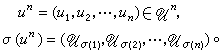 如U0的生成矩阵Gk×n=(Ik,Gk×(n-k)),则称U0为组织码;其中Ik为k阶幺矩阵。任何(n,k)线性码必等价于一个组织码。如
如U0的生成矩阵Gk×n=(Ik,Gk×(n-k)),则称U0为组织码;其中Ik为k阶幺矩阵。任何(n,k)线性码必等价于一个组织码。如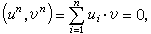 则称un⊥vn;其中和积运算均在Fq域中。如对任何un∈U0,vn⊥un,则称vn⊥U0,称
则称un⊥vn;其中和积运算均在Fq域中。如对任何un∈U0,vn⊥un,则称vn⊥U0,称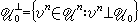 为U0的对偶码,这时U
为U0的对偶码,这时U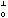 为(n,n-k)码且生成矩阵为
为(n,n-k)码且生成矩阵为 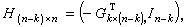 式中
式中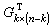 为
为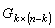 的转置矩阵,称H为U0的校验矩阵。
的转置矩阵,称H为U0的校验矩阵。如U0的生成矩阵是一个循环矩阵,即
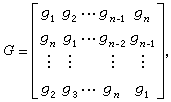 则称U0为一个循环码,
则称U0为一个循环码,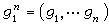 为U0的生成元。典型的循环码是BCH码:如记α为
为U0的生成元。典型的循环码是BCH码:如记α为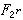 域的本原元,e为
域的本原元,e为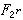 域的幺元,则
域的幺元,则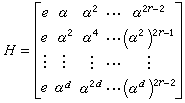 为一个dr×2r-1阶矩阵,这里把α看作一个2元r维列向量。如U0的校验矩阵是(30)的H,则称U0是BCH码。它是一个2元(2r-1,2r-1-dr)码,d称为设计距离,其纠错能力为
为一个dr×2r-1阶矩阵,这里把α看作一个2元r维列向量。如U0的校验矩阵是(30)的H,则称U0是BCH码。它是一个2元(2r-1,2r-1-dr)码,d称为设计距离,其纠错能力为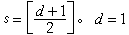 时的 BCH码为汉明码。循环码的编码器可通过移位寄存器实现,对BCH码与汉明码的纠错译码算法也比较简单。重要的循环码还有戈帕码与R-S码。
时的 BCH码为汉明码。循环码的编码器可通过移位寄存器实现,对BCH码与汉明码的纠错译码算法也比较简单。重要的循环码还有戈帕码与R-S码。如 U*为 Fq域上的一个无限维线性空间,元
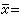
 的非零分量有限,设U0是U*的线性空间,生成矩阵为
的非零分量有限,设U0是U*的线性空间,生成矩阵为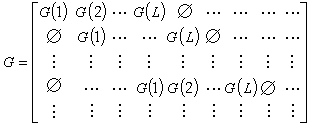 ,式中
,式中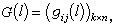 则称 U0为卷积码;
则称 U0为卷积码;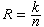 为码率;矩阵g=(G(1),G(2),…,G(L))为生成元。这时
为码率;矩阵g=(G(1),G(2),…,G(L))为生成元。这时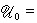
 其中M*为全体嚗=(m1,m2,…)向量的集合,mi∈Fq,且非零元有限。卷积码的编码可由移位寄存器实现,而译码可由序贯译码实现。重要的译码方法有费诺译码法、维特比译码法等。
其中M*为全体嚗=(m1,m2,…)向量的集合,mi∈Fq,且非零元有限。卷积码的编码可由移位寄存器实现,而译码可由序贯译码实现。重要的译码方法有费诺译码法、维特比译码法等。保密学 这是一门古老而又神秘的学科。在古代,人们就知道用密写、暗语来传递机密。随着无线电通信的发展,它形成了一门学科,在战争中起重要作用。近年来,计算机的广泛应用为保密学提出了一系列新的课题,如保密系统的标准化、加密密钥的公开化等。近代保密学包括密码编码学和密码分析学两大内容,讨论的还有网络系统加密、密钥管理等问题。
一个保密系统是由明文、密文、密钥空间所构成。明文就是普通信源;密文是伪装后的明文,非授权者一般不能了解它的内容;密钥就是加密运算,密钥空间是可能使用的加密密钥。建立一个保密系统必须遵循一些原则,例如,它在理论上或实际计算上具有不可破性,系统在使用过程中部分信息泄露不危及系统在以后使用中的机密,加密设备的简易性与计算机的匹配性,密钥使用与更换的方便性等。
经典的加密方法主要是置换法,如单字母的卡萨尔系统与多字母的维基尼系统。第二次世界大战中许多国家使用转轮加密机,这是一种利用转动机械的加密装置。DES (数据加密标准)体制是由美国国家标准局公布、于1977年7月15日生效的一种标准加密体制,它是由对64比特数的一系列标准运算构成,因此它的设备与使用具有通用化的特征。公开密钥体制是一种正在研究中的加密体制,其主要特点是加密密钥与解密密钥不同且由加密密钥不能直接算出解密密钥。每个用户可将自己的加密密钥象电话号码本那样公开,任何人可根据这个密钥将消息通知这个用户,其他用户由于不了解该用户的解密密钥,因此无法了解这些消息的内容。重要的公开密钥体制有对数运算体制、背包体制与RSA体制。
量子信号的检测与估值 经典的信号检测、估值理论是一般信息论的一个重要组成部分。它的问题背景来自雷达信号的一系列处理问题,涉及信息论、统计理论与随机过程理论等学科。近些年,在光通信中,由于激光信号的量子性,出现了一系列关于量子信号、激光信号的检测与估值问题。因此该理论是经典检测理论与量子场理论的综合问题,在激光通信中有着十分重要的意义。
参考书目
万哲先著,《代数和编码》,科学出版社,北京,1980。
R.G.Gallager,InforMation Theory and Reliable Com-munication, John Wiley & Sons,New York, 1968.R.J.McEliece,The Theory of InforMation and Co-ding-A MatheMatical Framework for Communication,Addison-Wesley, Reading, Mass., 1977.
T.Berger,rate Distortion Theory, Prentice-Hall, Eng-lewood Cliffs, N. J., 1971.
A.G.Konheim,Cryptography, A Primer, John Wiley& Sons, New York, 1981.
C.W.Helstrom,Quantum Detection and EstiMation Theory, AP, New York, 1976.