亥姆霍兹方程(卷名：物理学)
Helmholtz equation
在数学上具有(墷2+k2)ψ =f形式的双曲型偏微分方程。式中墷2为拉普拉斯算子，在直角坐标系中为
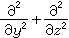；ψ为待求函数;k2为常数；f为源函数。当f等于零时称为齐次亥姆霍兹方程;f不等于零时称为非齐次亥姆霍兹方程。在电磁学中，当函数随时间作简谐变动时，波动方程化为亥姆霍兹方程。例如，在均匀各向同性媒质中，电场和磁场强度满足下述波动方程
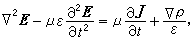(1)
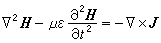。 (2)当一个函数F(x，y，z，t)随时间作简谐变动时，可以表成F(x，y，z)ejwt的形式，这时д/дt相当于jω，д2/дt2相当于－ω2，代入式(1)、(2)，并利用电荷与电流之间的连续方程墷·J＝-дρ/дt，可得
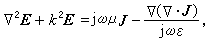(3)
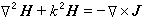， (4)式中k＝ω(με)┩，称为波数。在场强的非齐次亥姆霍兹方程中，右边的源函数比较复杂。若换用电磁势，源函数可得到简化。洛伦兹规范下，简谐变化的A和嗞满足下述非齐次亥姆霍兹方程
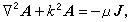(5)
(6)在没有源的区域，式(5)、(6)变为齐次亥姆霍兹方程
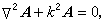(7)
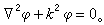(8)若此区域是有界的，例如在波导中，则因边界条件的限制，方程的解可以用离散的本征模式的线性组合来表示。每一模式的系数取决于源函数和待定函数的边值(见电磁场的边值问题)。