中国数学史(卷名：数学)
history of mathematics in China
数学是中国古代科学中一门重要的学科，它的历史悠久，成就辉煌。根据它本身发展的特点，可以分为五个时期：①中国古代数学的萌芽；②中国古代数学体系的形成；③中国古代数学的发展；④中国古代数学的繁荣；⑤中西方数学的融合。
中国古代数学的萌芽 原始公社末期，私有制和货物交换产生以后，数与形的概念有了进一步的发展，仰韶文化时期出土的陶器，上面已刻有｜，
，
，
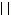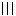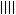等表示1，2，3，4的符号。《易·繫辞》中说:“上古结绳而治，后世圣人易之以书契。”这就是说，到原始公社末期，人们已开始用文字符号取代结绳记事了。西安半坡出土的陶器有用1～8个圆点组成的等边三角形和分正方形为100个小正方形的图案，半坡遗址的房屋基址都是圆形和方形(见彩图)。为了画圆作方，确定平直，人们还创造了规、矩、准、绳等作图与测量工具。据《史记·夏本纪》记载。夏禹治水时已使用了这些工具。
商代中期，在甲骨文中已产生一套十进制数字和记数法，其中最大的数字为三万；与此同时，殷人用十个天干和十二个地支组成甲子、乙丑、丙寅、丁卯等60个名称来记60天的日期。在周代，又把以前用阴(--)、阳(-)符号构成的八卦表示8种事物发展为六十四卦，表示64种事物。公元前1世纪的《周髀算经》 提到西周初期用矩测量高、深、广、远的方法，并举出勾股形的勾三、股四、弦五以及环矩可以为圆等例子。《礼记·内则》篇提到西周贵族子弟从九岁开始便要学习数目和记数方法，他们要受礼、乐、射、驭、书、数的训练，作为“六艺”之一的数已经开始成为专门的课程。
春秋战国之际，筹算已得到普遍的应用。筹算记数法已使用十进位值制。约公元前 4世纪的《墨经》描述这种记数法时说：“一少于二而多于五。说在建位。”这就是说，一在个位少于二，在十位就多于五，每个数字的大小除由它本身所表示的数值决定外，还要看它在整个数中所处的位置。根据后来约公元 4世纪的《孙子算经》的记载，任何数都是由九个纵排数字｜
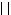
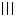
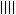
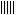
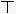
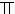
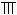和九个横排数字－＝
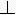
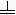
按个、百、万等用纵筹，十、千等用横筹来表示，零用空位表示。这种记数法对世界数学的发展是有划时代意义的。这个时期的测量数学在生产上有了广泛应用，在数学上亦有相应的提高。在《考工记》中，已分别用矩、勾、倨、宣、、柯、磬析表示直角、锐角、钝角、45°、67°30′、101°15′、151°52.5′（或135°），还有用规(圆周)的部分(圆弧)来表示刀和弓的大小，例如“合六而成规”，“合九而成规”，“合七而成规”等等。战国时期的百家争鸣也促进了数学的发展，尤其是对于正名和一些命题的争论直接与数学有关。名家认为经过抽象以后的名词概念与它们原来的实体不同，他们提出“矩不方，规不可以为圆”，把“大一”（无穷大）定义为“至大无外”，“小一”（无穷小）定义为“至小无内”，还提出“轮不辗地”、“南方无穷而有穷”、“一尺之棰，日取其半，万世不竭”等命题。而墨家则认为名来源于物，名可以从不同方面和不同深度反映物。墨家给出一些数学定义。例如，圆：一中同长也（从中心到周界有相同长度）；方：柱隅四殻也（四边四角皆正）；平：同高也（高度相等）；直：参也（三点相齐）；次（相切）：无间而不相樱也（既无大小又不相合）；端(点)：体之无厚而最前者也(部分中没有大小并处于最前缘者)，等等。墨家提出“环俱抵”（圆环转动时每一点都与地面接触而形成一根直线）来反驳名家的“轮不辗地”，次的定义显然来源于此。他们认为，在区域的前缘连一根线也容纳不下（域不容尺）称为“有穷”；不论区域多大，在其前缘总能容下一线之宽(莫不容尺)，称为“无穷”。因此在墨家看来，一个具体的空间不能既是“有穷”，又是“无穷”的。墨家也不同意“一尺之棰”的命题，提出一个“非半”的命题来进行反驳：将一线段按一半一半地无限分割下去，就必将出现一个不能再分割的“非半”，这个“非半”就是点（非半弗则不动，说在端）。名家的命题论述了有限长度可分割成一个无穷序列，墨家的命题则指出了这种无限分割的变化和结果。名家和墨家的数学定义和数学命题的讨论对中国古代数学理论的发展是很有意义的。中国古代数学体系的形成 秦汉是封建社会的上升时期，经济和文化均得到迅速发展。中国古代数学体系正是形成于这个时期，它的主要标志是算术已成为一个专门的学科以及《九章算术》为代表的数学著作的出现。《汉书·艺文志》载有《许商算术》2卷和《杜忠算术》16卷，但均已失传。1983年12月在湖北江陵张家山出土一本西汉初年的《算数书》，收有许多应用的数学问题。现有传本的著作是公元前1世纪的《周髀算经》和公元1世纪的《九章算术》(见彩图)。《周髀算经》是一部讲述盖天学说的天文著作，书中有较复杂的开方、分数运算和勾股定理的应用等数学问题。
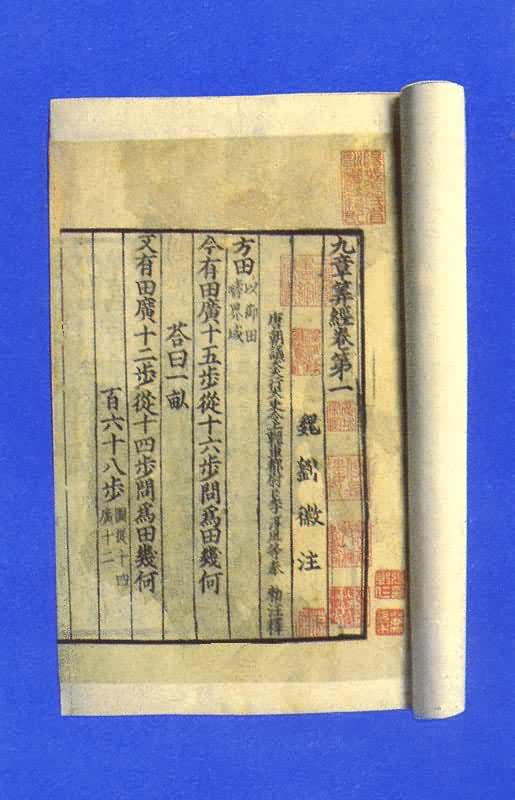
《九章算术》是战国、秦、汉封建社会创立并巩固时期数学发展的总结，就其数学成就来说，堪称是世界数学名著。例如分数四则运算，今有术(西方称三率法)，开平方与开立方（包括二次方程数值解法），盈不足术（西方称双设法），各种面积和体积公式，线性方程组解法，正负数运算的加减法则，勾股形解法（特别是勾股定理和求勾股数的方法）等，水平都是很高的，其中方程组解法和正负数加减法则在世界数学发展上是遥遥领先的。就其特点来说，它形成了一个以筹算为中心、与古希腊数学完全不同的独立体系。
《九章算术》有几个显著的特点：①采用按类分章的数学问题集的形式；②算式都是从筹算记数法发展起来的，这些算式表示法紧密地依赖于数字在图式上的位置；③以算术、代数为主，几何也是偏重于量的计算，很少涉及图形的性质;④重视应用，缺乏理论阐述。这些特点同当时社会条件与学术思想有关。秦汉时期，一切科学技术要求密切为当时确立和巩固封建制度以及发展社会生产服务。秦始皇为了推行中央集权制，重用荀派儒学和法家刑名之学，甚至不惜采取焚书坑儒的措施。汉武帝以后，为了巩固封建政权，接受董仲舒“罢黜百家，独尊儒术”的意见，把经董仲舒改造的儒家思想作为统治阶级的思想。西汉末年著名学者刘歆曾经谈到对数学的看法，他说:“夫推历、生律、制器、规圆、矩方、权重、衡平、准绳、嘉量、探赜索隐，钩深致远，莫不用焉。度长短者不失毫厘，量多少者不失圭撮，权轻重者不失黍絫。”刘歆这种强调数学应用的看法是具有代表性的。最后成书于东汉初年的《九章算术》，排除了战国时期在百家争鸣中出现的名家和墨家重视名词定义与逻辑的讨论，偏重于与当时生产、生活密切相结合的数学问题及其解法，这与当时社会的发展情况是完全一致的。
《九章算术》在隋唐时期曾传到朝鲜、日本，并成为这些国家当时的数学教科书。它的一些成就如十进位值制、今有术、盈不足术等还传到印度和阿拉伯，并通过印度、阿拉伯传到欧洲，促进了世界数学的发展。
中国古代数学的发展 魏、晋数学的发展 魏、晋时期出现的玄学，不为汉儒经学束缚，各抒己见，思想比较活跃；它诘辩求胜，又能善于运用逻辑思维，分析义理。这些都有利于数学从理论上加以提高。吴国赵爽注《周髀算经》，汉末魏初徐岳撰《九章算术》注 2卷（已失传），魏末晋初刘徽撰《九章算术》注10卷(263)、《九章重差图》1卷（已失传）都是出现在这个时期，赵爽与刘徽的工作为中国古代数学体系奠定了理论基础。
赵爽是中国古代对数学定理和公式进行证明与推导的最早的数学家之一。他在《周髀算经》书中补充的“勾股圆方图及注”和“日高图及注”是十分重要的数学文献。在“勾股圆方图及注”中他提出用弦图证明勾股定理和解勾股形的5个公式；在“日高图及注”中，他用图形面积证明汉代普遍应用的重差公式，赵爽的工作是带有开创性的，在中国古代数学发展中占有重要地位。
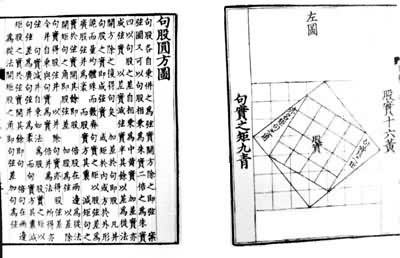
刘徽约与赵爽同时，他继承和发展了战国时期名家和墨家的思想，主张对一些数学名词特别是重要的数学概念给以严格的定义，认为对数学知识必须进行"析理"，才能使数学著作简明严密，利于读者。他的《九章算术》注不仅是对《九章算术》的方法、公式和定理进行一般的解释和推导，而且在论述的过程中有很大的发展。例如，刘徽从率（后称为比）的定义出发论述了分数运算和今有术的道理，并推广今有术得到合比定理，他根据率、线性方程组和正负数的定义阐明方程组解法中消元的道理，指出方程式个数少于未知数个数时，方程组的解只能是一个比值；在一个方程式中，正与负可以同时变号；减法消元和加法消元可以统一为一种方法。刘徽指出，在开方求得整数后，还可以继续开方，“求其微数”。这不仅解决了求无理根的问题，而且提出了十进小数的方法。他创造割圆术，利用极限的思想证明圆的面积公式，并首次用理论的方法算得圆周率
和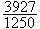
。他提出用无穷分割的方法证明直角方锥与直角四面体的体积之比恒为2:1，解决了一般立体体积的关键问题。在证明方锥、圆柱、圆锥、圆台的体积时，刘徽实际上应用了下列公理：等高的两立体，若其任意同高处的水平截面积成比例，则这两立体体积亦成同样的比例；并根据这个公理，指出球的体积与其外切“牟合方盖”(两个等半径的圆柱正交的共同部分，（见彩图)的体积之比为π:4，为彻底解决球的体积提出了正确的途径。
刘徽在数学理论上取得如此重大的成就，除和他那个时代重视理论探讨的学术风气有关外，作为个人，有两点是十分重要的。第一，反对今文经学中的阴阳奇偶学说。在《九章算术·少广》章开立圆术注中，刘徽批评张衡在推导球的体积时，为了附会阴阳奇偶的学说而不顾疏密是一种弊病。第二，反对古文经学的繁琐和守旧思想。在《九章算术·方田》章圆田术注和《九章算术·方程》章末题注中他批评当时学者的"踵古"思想和“胶柱调瑟”不知变通的思想，认为数学如“疱丁之理”，应该讲求技巧，见简即用。
南北朝数学的发展 东晋以后，中国长期处于战争和南北分裂的状态。在北方，由于当时社会的需要，在《九章算术》的基础上，数学仍在继续发展。《孙子算经》、《夏侯阳算经》（已失传）、《张丘建算经》就是这个时期的著作。从留传下来的《孙子算经》与《张丘建算经》来看，它们仍依《九章算术》的体例，甚至有些题目也是为了解释《九章算术》的算法。也有一些难题和解法超出《九章算术》的范围，并对后来数学的发展有着相当的影响，例如一次同余式组解法，等差级数求和、求公差、求项数的方法和不定方程解法等。
祖冲之父子的工作则是经济文化南移以后南方数学发展的具有代表性的工作，他们在《九章算术》刘徽注的基础上，把传统数学大大向前推进了一步。根据史书的记载，祖冲之曾经注解《九章算术》，并与他的儿子祖暅共撰《缀术》六卷。这些著作均已失传。在《隋书·律历志》与李淳风《九章算术》注等零星记载中，他们的数学工作主要有下列几项。
① 圆周率 据推测， 祖冲之在刘徽割圆术的基础上，算出圆内接正6144边形和正12288边形的面积，从而得到 3.1415926< π <3.1415927。他又创造了新的方法，得到圆周率两个分数值，即约率22/7和密率355/113。祖冲之这一工作，使中国在圆周率计算方面，比西方领先约一千年之久。
② 祖暅公理和球体积 祖暅总结了刘徽的有关工作，提出“幂势既同则积不容异”即等高的两立体，若其任意高处的水平截面积相等，则这两立体体积必相等，这就是著名的祖暅公理。祖暅应用这个公理，解决了刘徽尚未解决的球体积公式。
③ 二次与三次方程 《隋书· 律历志》在叙述祖冲之的圆周率以后说：“又设开差幂，开差立，兼以正负参之。指要精密，算氏之最者也。”中国古代称正系数的二次与三次方程解法为开带从平方和开带从立方，祖冲之用“差幂”取代带从平方，用“差立”取代带从立方，应指包括负系数在内的二次与三次方程的解法，因为只有负系数的方程在开方时才需“兼以正负参之”。这一数学工作确实是划时代的重大成就。
祖冲之父子这些成就也和他们的数学思想有关。和刘徽一样，祖冲之强烈反对踵古，他在大明六年(462)和戴法兴辩论历法时，提出对古代一切历法理论都要加以核验，决不“虚推古人”。他重视实践，为了制定一个准确的历法，他不辞劳苦，长期进行观测。他认为日、月、五星运行的速度“非出神怪，有形可验，有数可推”。祖暅也十分重视数学思维和数学推理，他提出，如果不能从已知条件直接导出结论时，可以假借相同的条件来进行分析（控远以演类，借况以折微）；在谈到球体积公式还没有解决时说：“夫岂难哉，抑末之思也。”言外之意是，他的球体积公式是经过逻辑思维推得的。
隋、唐数学的发展 隋炀帝好大喜功，大兴土木，客观上促进了数学的发展。唐初王孝通的《缉古算经》，主要是讨论土木工程中计算土方、工程的分工、验收以及仓库和地窖的计算问题，反映了这个时期数学发展的情况。已知不等高的长方棱台体积和上底、下底、高、长的差，求上底、下底、高和长是一个三次方程问题。王孝通的主要贡献是在《九章算术》的基础上，在不用数学符号的情况下，立出数字三次方程，不仅解决了当时社会的需要，也为后来天元术的建立打下基础。此外，对传统的勾股形解法，他也有所发展，已知勾股形的勾股积与勾股差（或股弦差），求勾股，这类问题王孝通也是用数字三次方程解决的（见王孝通）。
唐初封建统治者继承隋制，656年在国子监设立算学馆，设有算学博士和助教，学生30人。由太史令李淳风等编纂注释《算经十书》，作为算学馆学生用的课本。明算科考试亦以这些算书为准。李淳风等编纂的《算经十书》，对保存数学经典著作、为数学研究提供文献资料方面是很有意义的;他们给《周髀算经》、《九章算术》以及《海岛算经》所作的注解，对读者是有帮助的(见《算经十书》)。
隋唐时期，由于历法的需要，天算学家创立了二次函数的内插法，丰富了中国古代数学的内容。206年，为了确定合朔时刻，刘洪在《乾象历》中首次提出用一次内插公式来确定月球在n+s（n为正整数，s<1）日共行的度数。600年，隋代天文学家刘焯在《皇极历》中提出一个推算日、月、五星视行度数的等间距二次内插公式。727年一行（张燧，683～727）在他的《大衍历》中又提出一个不等间距的二次内插公式。唐代其他历法，都应用内插法进行计算。
计算技术的改革 算筹是中国古代的主要计算工具，它具有简单、形象、具体等优点，但也存在布筹占用面积大，运筹速度加快时容易摆弄不正而造成错误等缺点，因此很早就开始进行改革。现传本《数术记遗》（题东汉徐岳撰，北周甄鸾注）载有“积算”、“太乙”、“两仪”、“三才”、“五行”、“八卦”、“九宫”、“运筹”、“了知”、“成数”、“把头”、“龟算”、“珠算”、“计数”等14种算法，反映了这种改革的情况。其中“太乙算”、“两仪算”、“三才算”和“珠算”都是用珠的槽算盘，在技术上是一项重要的改革。尤其是“珠算”，它继承了筹算五升十进与位值制的优点，又克服了筹算纵横记数与置筹不便的缺点，优越性十分明显。但由于当时乘除算法仍然不能在一个横列中进行。算珠还没有穿档，携带不方便，因此仍没有普遍应用。
唐中期以后，商业繁荣，数字计算增多，迫切要求改革计算方法，从《新唐书》等文献留下来的算书书目，可以看出这次算法改革主要是简化乘、除算法，书目中提到的“一位算法”、“求一”、“得一”的内容就是用分解因数的方法；化多位乘除为个位乘除；或用折半、加倍、退位的方法把乘除数化为首位是1的数，从而变乘除为加减。现传本《夏侯阳算经》记有很多这样的例子，例如“九因五添”、“添四四”、“身外减二”、“隔位加二”、“损一位”等等，唐代的算法改革使乘除法可以在一个横列中进行运算，它既适用于筹算，也适用于珠算。中国古代数学的繁荣 960年，北宋王朝的建立结束了五代十国割据的局面。北宋的农业、手工业、商业空前繁荣，科学技术突飞猛进，火药、指南针、印刷术三大发明就是在这种经济高涨的情况下得到广泛应用。1084年秘书省第一次印刷出版了《算经十书》。1213年鲍澣之又进行翻刻。这些情况为数学发展创造了良好的条件。从11～14世纪约300年期间，出现了一批著名的数学家和数学著作，如贾宪（11世纪中期）的《黄帝九章算法细草》(已失传)，刘益(12世纪中期)的《议古根源》（已失传），秦九韶的《数书九章》 (1247)，李冶的《测圆海镜》 (1248)和《益古演段》 (1259)，杨辉的《详解九章算法》(1261)、《日用算法》（1262）和《杨辉算法》(1274～1275)，朱世杰的《算学启蒙》（1299）和《四元玉鉴》 (1303)等，很多领域都达到古代数学的高峰。其中一些成就也是当时世界数学的高峰。
增乘开方法与贾宪三角（二项系数表） 从开平方、开立方到4次以上的开方，在认识上是一个飞跃，实现这个飞跃的是贾宪。杨辉在《九章算法纂类》中载有贾宪“增乘开平方法”、“增乘开立方法”；在《详解九章算法》中载有贾宪的“开方作法本源”图（见彩图）
“增乘方法求廉草”和用增乘开方法开 4次方的例子。根据这些记录可以确定贾宪已发现二项系数表，创造了增乘开方法。这两项成就对整个宋元数学发生重大的影响，其中贾宪三角比巴斯卡三角形早600多年。高次方程数值解法 把增乘开方法推广到数字高次方程（包括系数为负的情形）解法的是刘益（12世纪中期）。《杨辉算法》中《田亩比类乘除捷法》卷下介绍了原书中22个二次方程和1个四次方程，后者是用增乘开方法解三次以上的高次方程的最早例子。秦九韶是高次方程解法的集大成者，他在《数书九章》中收集了21个用增乘开方法解高次方程（最高次数为10）的问题。为了适应增乘开方法的计算程序，秦九韶把常数项规定为负数。他把高次方程解法分成各种类型，如：n次项系数不等于1的方程，奇次幂系数均为零的方程，进行x=y+с代换后常数项变号的方程与常数项符号不变而绝对值增大的方程等。方程的根为非整数时，秦九韶采取继续求根的小数，或用减根变换方程各次幂的系数之和为分母、常数为分子来表示根的非整数部分，这是《九章算术》和刘徽注处理无理数方法的发展。在求根的第 2位数时，秦九韶还提出以一次项系数除常数项为根的第 2位数的试除法。秦九韶的方法比霍纳方法早500多年。
高阶等差级数求和 高阶等差级数求和起源于沈括的"隙积术"。沈括在《梦溪笔谈》卷十八中提出，用棋子之类的东西堆成长方垛，棋子总数为
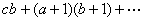
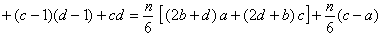(αb)是第一层的个数，сd是第n层的个数)。杨辉在《详解九章算法》中讨论了上述垛积的 3个特例。即方亭垛(α＝b，с＝d)、方锥垛(α=b=1，с=d=n)和三角垛
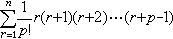
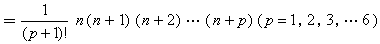。朱世杰把高阶等差级数求和问题与二项系数表结合起来，得到三角形垛
和岚形垛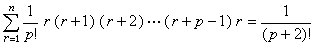
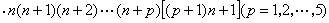。内插法 元代天文学家王恂、郭守敬等在《授时历》(1280)中解决了三次函数的内插值问题。秦九韶在“缀术推星”题、朱世杰在《四元玉鉴》“如象招数”题都提到内插法（他们称为招差术），朱世杰得到一个四次函数的内插公式。
一次同余式组解法 《孙子算经》“物不知数”题已提到一次同余式组解法的例子，秦九韶把它一般化。在这个方法中有一个必须解决的关键问题是求同余式kiGi呏1(mod αi)中的ki，式中
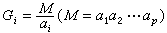。秦九韶在《数书九章》大衍类里，用更相减损的方法给出ki一个计算程序，完满地解决了这个问题，此外，秦九韶还讨论了模数αi是收数(小数)、通数(分数)、元数（一般正整数）、复数（10n的倍数）非两两互素的情形，并分别给出变上述4种数为两两互素的模数的方法。高次方程立法 用天元（相当于现在的 x）作为未知数符号，立出高次方程，古代称为天元术。这是中国数学史上首次引入符号，并用符号运算来解决建立高次方程的问题。现存最早的天元术著作是李冶的《测圆海镜》。李冶在一次项系数右旁记一“元”字（或在常数项右旁记一“太”字）。元以上的系数分别表示各正次幂，元以下的系数表示常数和各负次幂（在《益古演段》中又把这个次序倒转过来）。建立方程的具体方法是，根据问题的已知条件，列出两个相等的多项式p1(x)和p2(x)，令二者相减，即得一个数字高次方程。若其中一个多项式是分式多项式，如
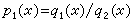，李冶则变另一多项式p2(x)为
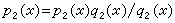，使二者相减时消去分式多项式的分母，得 
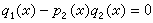。这是刘徽关于率的概念在多项式运算中的应用与发展。高次联立方程组 从天元术推广到二元、三元和四元的高次联立方程组，是宋元数学家的又一项杰出的创造。祖颐在《四元玉鉴》后序中提到，平阳李德载《两仪群英集臻》有天、地二元，霍山刘大鉴《乾坤括囊》有天、地、人三元。燕山朱汉卿“按天、地、人、物立成四元”。前二书已失传，留传至今并对这一杰出创造进行系统论述的是朱世杰的《四元玉鉴》。朱世杰的四元高次联立方程组表示法无疑是在天元术的基础上发展起来的，他把常数放在中央。四元的各次幂放在上、下、左、右四个方向上，其他各项放在四个象限中。朱世杰的最大贡献是提出四元消元法。其方法是先择一元为未知数，其他元组成的多项式作为这未知数的系数，列成若干个一元高次方程式，然后应用互乘相消法逐步消去这一未知数。重复这一步骤便可消去其他未知数，得到一个一元高次方程。最后用增乘开方法求解。这是线性方法组解法的重大发展。朱世杰的方法比西方同类方法早400多年。
勾股形解法 勾股形解法在宋元时期有新的发展，朱世杰在《算学启蒙》卷下提出已知勾弦和、股弦和求解勾股形的方法， 补充了《九章算术》的不足。 李冶在《测圆海镜》对勾股容圆问题进行了详细的研究，得到一系列的结果。他把容圆勾股形分成14个相似的勾股形，除按传统的方法给出这些勾股形的名称外，还用文字作符号来表示，与现今用字母A，B，C，…表示几何图形相似。从14个勾股形中，李冶得到692条“识别杂记”，阐明各勾股形的线段之间与线段的和、差、积之间的关系。除原有的勾股容圆外，李冶得到勾上容圆、股上容圆、弦上容圆、勾股上容圆、勾外容圆、股外容圆、弦外容圆、勾外容圆半、股外容圆半等9个容圆公式，大大丰富了中国古代几何学的内容。
弧矢割圆术 已知黄道与赤道的夹角和太阳从冬至点向春分点运行的黄经余弧，求赤经余弧和赤纬度数，是一个解球面直角三角形的问题。传统历法都是用内插法进行计算。元代王恂、郭守敬等则用传统的勾股形解法、沈括的会圆术(已知弦、矢、半径求弧长的近似公式)和天元术解决了这个问题。由于王恂、郭守敬求直径时用圆周率3以及沈括的公式是一个近似公式，因此结果不够精确。除此以外，整个推算步骤是正确无误的。从数学意义上讲，这个方法开辟了通往球面三角法的途径。
纵横图 纵横图又称幻方，根据《乾凿度》和东汉郑玄注，至迟在汉代已有一个三行纵横图。宋元时期，纵横图研究有了很大发展，杨辉在《续古摘奇算法》中记录了这方面的成就。杨辉指出，九宫图是一个从1～32的9个自然数排成三行三列，其行、列或对角线之和均为15的三行纵横图。这种图可以推广到从 1到n2的情形，它的行、列或对角线之和为n(1+n2)/2。他还列出四行、五行、六行、七行、八行、九行、十行8个纵横图，并指出三行和四行纵横图的构造方法。杨辉的这一工作为这个领域的研究开辟了道路。
小数 现传本《夏侯阳算经》已有化名数为十进小数的例子。宋元时代，这种十进小数有了广泛应用和发展，秦九韶用名数作为小数的符号，例如18.56寸表示如图1;李冶则依靠算式的位置表示，例如－8.25x2+2.673=0表示如图2。杨辉和朱世杰的化斤价为两价的歌诀，是小数的具体应用。
珠算的出现 中国古代计算技术改革的高潮也是出现在宋元时期。宋元明的历史文献中载有大量这个时期的实用算术书目，其数量远比唐代为多。改革的主要内容仍是乘除法。“留头乘”最早见于朱世杰《算学启蒙》。“九归”最早出现在沈括的《梦溪笔谈》，杨辉在《乘除通变本末》(1274)、朱世杰在《算学启蒙》中进一步把它完善。“归除”最早见于《算学启蒙》，“撞归”、“起一”是朱世杰首先提出来的，丁巨（著有《丁巨算法》，1355）、何平予（著有《详明算法》，1373）和贾亨（著有《算法全能集》）把它具体化。“留头乘”与“归除”的出现，使乘除法不需任何变通便可在一个横列里进行，与现今珠算的方法完全一样。与算法改革的同时，穿珠算盘在北宋已可能出现。但如果把现代珠算看成是既有穿珠算盘，又有一套完善的算法和口诀，那么应该说它最后完成于元代。
宋元数学的繁荣，是社会经济发展和科学技术发展的必然结果，是传统数学发展的必然结果。此外，数学家们的科学思想与数学思想也是十分重要的。宋元数学家都在不同程度上反对理学家的象数神秘主义。李冶曾批评朱熹著作，说它不通的地方很多。他指出，说数学难认识是可以的，但说数学不能认识就不对；他认为数学来源于自然界，“苟能推自然之理”就可以“明自然之数”。秦九韶虽曾主张数学与道学同出一源，但他后来也认识到，“通神明”的数学是不存在的，只有“经世务类万物”的数学。莫若在《四元玉鉴》序文中提出的“用假象真，以虚问实”则代表了朱世杰高度抽象思维的思想方法，杨辉对纵横图结构进行研究，揭示出洛书的本质，有力地批判了象数神秘主义。所有这些，无疑是促进数学发展的重要因素。
中、西方数学的融合 明代进入了封建社会的晚期，封建统治者实行极权统治，宣传唯心主义哲学，施行八股考试制度。在这种情况下，除珠算外，数学发展逐渐衰落。16世纪末以后，西方初等数学陆续传入中国，使中国数学研究出现一个中西融合贯通的局面。鸦片战争以后，近代数学开始传入中国，中国数学便转入一个以学习西方数学为主的时期，直到19世纪末与20世纪初，近代数学研究才真正开始。
珠算的普及 从明初到明中叶，商品经济有所发展，和这种商业发展相适应的是珠算的普及。明初《魁本对相四言杂字》(1371)和《鲁班木经》(15世纪上半叶)的出现，说明珠算已十分流行。前者是儿童看图识字的课本，后者把算盘作为家庭必需用品列入一般的木器家具手册中。随后，珠算著作也陆续出现。如吴敬《九章详注比类算法大全》（1450）、王文素《古今算学宝鉴》(1524)、徐心鲁《盘珠算法》(1573)、柯尚迁《数学通轨》(1578)、朱载堉的《算学新说》（1584）、程大位《直指算法统宗》(1592)等。随着珠算的普及，珠算算法和口诀也逐渐趋于完善。例如王文素和程大位增加并改善撞归、起一口诀；徐心鲁和程大位增添加、减口诀并在除法中广泛应用归除，从而实现了珠算四则运算的全部口诀化；朱载堉和程大位把筹算开平方和开立方的方法应用到珠算，程大位用珠算解数字二次、三次方程等等。程大位的著作在国内外流传很广，影响很大。
早期传入的西方数学 1582年意大利传教士利玛窦到中国，1607年以后，先后与徐光启翻译《几何原本》前6卷(1607)、《测量法义》1卷(1607～1608)，与李之藻编译《圜容较义》(1608)和《同文算指》(1613)。1629年，徐光启被礼部任命在历局督修历法，在他主持下，编译《崇祯历书》137卷。《崇祯历书》主要是介绍欧洲天文学家第谷的地心学说，作为这一学说的数学基础，希腊的几何学，欧洲玉山若干的三角学以及纳皮尔算筹，伽利略比例规等计算工具也同时介绍进来。
在传入的数学中，影响最大的是《几何原本》。《几何原本》是现传的中国第一部数学翻译著作。绝大部分数学名词都是首创，其中许多至今仍在沿用。徐光启认为对它“不必疑”，“不必改”，“举世无一人不当学”。他所著的《测量异同》和《勾股义》，就是应用《几何原本》的逻辑推理方法论证中国的勾股测望术。他主编的《崇祯历书》，天文学和数学基本理论占全书30％，充分说明他对理论的重视。《几何原本》是明清两代数学家必读的数学书，对他们的研究工作也颇有影响。其次，应用最广的是三角学。介绍西方三角学的著作有邓玉函编译的《大测》2卷(1631)、《割圆八线表》6卷和罗雅谷的《测量全义》10卷（1631）。《大测》主要说明三角八线（正弦、余弦、正切、余切、正割、余割、正矢、余矢）的性质，造表方法和用表方法。《测量全义》除增加一些《大测》所缺的平面三角外，比较重要的是积化和差公式和球面三角（直角三角形的弧与角的关系式和一般三角形的正弦定理和余弦定理）。所有这些，在当时历法工作中都是随译随用的。
中西数学的会通 1646年，波兰传教士穆尼阁来华，跟随他学习西方科学的有薛凤祚、方中通等。穆尼阁去世后，薛凤祚据其所学，编成《历学会通》，想把中法西法融会贯通起来。《历学会通》中的数学内容主要有《比例对数表》1卷（1653）、《比例四线新表》1卷和《三角算法》1卷(1653)。前两书是介绍英国数学家 J.纳皮尔和H.布里格斯发明增修的对数。后一书除《崇祯历书》介绍的球面三角外，尚有半角公式、半弧公式、德氏比例式（Delambres analogies）、 纳氏比例式(Nepiers analogies)等。方中通所著《数度衍》(1641)，对对数理论进行解释。对数的传入是十分重要，它在历法计算中立即就得到应用。
清初学者研究中西数学有心得而著书传世的很多，影响较大的有王锡阐《图解》1卷，梅文鼎《梅氏丛书辑要》60卷(其中数学著作13种共40卷)，年希尧《视学》2卷等。王锡阐的工作主要是证明两角和、差的正弦和余弦公式。为了证明上述公式，他对涉及的名词概念都逐一加以定义，引入“折”的概念取代角;由于缺乏直角坐标系的概念，在证明时他还把两弧和两弧的和差分为小于象限或大于象限的各种情形，方法是独具一格的。梅文鼎是集中西数学之大成者。他对传统数学中的线性方程组解法、勾股形解法和高次幂求正根方法等方面进行整理和研究，使濒于枯萎的明代数学出现了生机，在介绍西方数学中有校正、证明和补充。例如：校正了罗雅谷关于比例规叙述中的错误，证明三角学中没有证明的公式和定理等。梅文鼎认为传统的勾股形解法就是西方的几何学和三角学，他用勾股形解法的公式证明《几何原本》前6卷的15个定理，用勾股方法证明球面直角三角形的边角关系公式。他创造一种直角射影的方法证明球面三角学的余弦定理。对《测量全义》介绍的 5种多面体公式，他证明了其中4种，其中关于二十面体的计算，他纠正了《测量全义》和罗雅谷的错误等。梅文鼎肯定数学来源于实际；对西方数学，他认为“技取其长而理唯其是”，“法有可采何论东西，理所当明何分新旧”，应该“去中西之见，以平心观理”，态度是比较正确的。年希尧的《视学》是中国第一部介绍西方透视学的著作。
清康熙皇帝十分重视西方科学，他除了亲自学习天文数学外，还培养了一些人才和翻译了一些著作。1712年康熙皇帝命梅瑴成任蒙养斋汇编官，会同陈厚耀、何国宗、明安图、杨道声等编纂天文算法书。1721年完成《律历渊源》100卷，以康熙“御定”的名义于1723年出版。其中《数理精蕴》53卷主要由梅瑴成负责，分上下2编，上编包括《几何原本》3卷、《算法原本》1卷，均译自法文著作；下编40卷，包括算术、代数、平面几何、平面三角、立体几何等初等数学，附有素数表、对数表和三角函数表。《数理精蕴》的基本内容除传统数学和早期传入的西方数学外，新传入的数学有借根方比例、“连比例”方法，椭圆面积和椭球体积以及计算尺、素数表等。由于它是一部比较全面的初等数学百科全书，并有康熙“御定”的名义，因此对当时数学研究是具有一定影响的。
1701年法国人杜德美带来J.格雷果里的“弧求正弦”、“弧求正矢”和I.牛顿的“圆径求周”三个无穷级数的公式，但没有证明。1800年前后，明安图、董祐诚、项名达各自依据《数理精蕴》提出的“连比例”方法，对这些级数进行研究，获得一些创造性结果。明安图著有《割圆密率捷法》4卷 (1774年由他的学生陈际新定稿)，他除了证明杜德美传入的 3个公式外，还创造“弧求通弦”、“弧求正矢”、“通弦求弧”、“正矢求弧”、“正弦求弧”、“正矢求弧” 6个新的公式。董祐诚著有《割圜连比例图解》2卷(1819)，他把明安图9个公式概括为“分弧通弦求全弧通弦”、“分弧中矢求全弧中矢”、“分弧通弦求通弧通弦”、“分弧中矢求通弦中矢”4个公式。1837年项名达又把董祐诚的4个公式概括为“分弧通弦求全弧通弦”、“分弧中矢求全弧中矢”两个公式。他著有《象数一原》6卷(1837，由戴煦续成)。著作后面附有《椭圆求周术》，正确地解决了椭圆求周长的问题。
戴煦对三角函数的幂级数公式和椭圆求周的问题也有研究，著有《外切密率》4卷(1852)，补充正切、余切、正割、余割四个幂级数公式。为了简化对数的计算，他创立了指数为任何有理数的二项式定理展开式，从而也得到对数函数的幂级数公式。这些成果记载在他著的《对数简法》2卷(1845)和《续对数简法》1卷(1846)中。
与戴煦同时，李善兰在1845年著有《方圆阐幽》1卷，《弧矢启秘》2卷与《对数探源》2卷。他创造尖锥术，并用它来论证二项平方根的幂级数公式，π的幂级数公式，“正弦求弧”、“正切求弧”、“弧求正弦”、“弧求正切”、“弧求正矢”、“弧求正割”等三角函数幂级数公式以及对数函数幂级数公式。所谓尖锥术是指对一切自然数n的乘方数 xn都可用线段长表示，它们可以积迭成 n乘尖锥面。这种尖锥面由相互垂直的底线、高(h)和凹向的尖锥曲线组成。其面积为
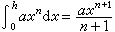。这种尖锥面表示法已具有解析几何的坐标表示的思想，求积法相当于幂函数的定积分公式。综上述可以看到，清代数学家对西方数学做了大量的会通工作，并取得许多独创性的成果。这些成果，如和传统数学比较，是有进步的，但和同时代的西方比较，则明显落后了。
传统数学的整理和研究 雍正即位(1723)以后，对外闭关自守，导致西方科学停止输入中国，对内对汉族士大夫实行高压政策。在这种情况下，一般学者既不能接触西方数学，又不敢过问经世致用之学，因而埋头于究治古籍。乾嘉年间逐渐形成一个以考据学为主的乾嘉学派。1773年开设四库全书馆，辑录《永乐大典》保存佚书和征集私家藏书，于1781年编成《四库全书》，先后收集到《算经十书》和宋元时期的数学著作。纂修兼分校官戴震（1724～1777）对《周髀算经》、《九章算术》、《孙子算经》、《五经算术》 4部著作详加校勘，改正许多误文夺字，对学者是有帮助的。随后，李潢(?～1811)著的《九章算术细草图说》9卷，《海岛算经细草图说》1卷和《辑古算经考注》2卷，李锐注的《数书九章》、《测圆海镜》和《益古演段》，沈钦裴著的《四元玉鉴细草》2 卷（1829）和罗士琳撰的《四元玉鉴细草》24卷(1834)都很有参考价值。
随着《算经十书》与宋元数学著作的收集与注释，出现了一个研究传统数学的高潮。其中能突破旧有框框并有发明创造的有焦循、汪莱、李锐、李善兰等。焦循在《加减乘除释》（1798）中，用甲、乙、丙、丁……等天干字表示具体的数，列出加、减、乘、除的几个基本定律，用这些符号和定律来说明古代算法原理，这在中国数学史上是一个创造。汪莱著有《衡斋算学》 7册(1796～1805)。在第五册(1801)中，他讨论了二次、三次方程有多少正根以及正根和系数的关系问题，得到与韦达定理相当的结果。在第七册(1805)中专门讨论三项方程xn-pxm+q=0（n>m 都是正整数，p、q都是正数），他用归纳法得到上述方程有正根的条件相当于
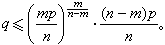1802年李锐见到汪莱的《衡斋算学》第五册算书后，写了“第五册算书跋”，提出 n次高次方程只有一个正根与多于一个正根和方程系数的符号有关，和得到一个正根后的(n-1)次方程的系数符号有关，他的结论基本上是正确的。在《开方说》(1817)中李锐进一步指出：高次方程系数符号变化一次的有1正根，变化二次的有2正根，变化三次的有3正根或1正根，变化四次的有4正根或2正根，所缺正根称为“无数”，“凡无数必两，无一无数者”。这些与笛卡儿的符号规则基本相同。他还指出：二次方程有2根，三次方程有3根或1根，四次方程有4根或2根（以上均包括负根）；若方程有正、负根，将方程系数的正负号隔位易之，则正负根互换符号；方程的重根与“无数”不同等等。汪莱、李锐的工作，和宋元时代的代数学比较是青出于蓝而胜于蓝的；和西方代数学比较，在时间上晚了一些，但他们的成果是在没有受到西方近代数学的影响下独立得到的。对朱世杰的垛积术进行研究并有重大成果的是李善兰，在《垛积比类》（约1859）中，李善兰创造了一个著名的恒等式：
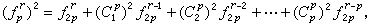式中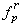
为朱世杰三角垛的一般项，
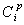是二项式定理系数。利用三角垛求和公式就得出一个中外驰名的三角自乘垛求和公式：
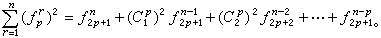他还得到三角变垛
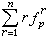、三角再变垛
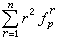和三角三变垛
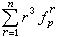的公式。与传统数学研究出现高潮的同时，阮元与李锐等编写了一部天文数学家传记──《畴人传》(1795～1810)。《畴人传》收集从黄帝时期到嘉庆四年(1799)已故的天文学家和数学家270余人(其中有数学著作传世的不足50人)和明末以来介绍西方天文数学的传教士 41人。这部著作全由“掇拾史书，荃萃群籍，甄而录之”而成，收集的完全是第一手的原始资料，在学术界颇有影响。
近代数学的传入 鸦片战争（1840）以后，西方近代数学开始传入中国。首先是英人在上海设立墨海书馆，介绍西方数学。第二次鸦片战争(1860)后，曾国藩、李鸿章等官僚集团开展“洋务运动”，也主张介绍和学习西方数学。1864年美国长老会教士狄考文于山东登州设立文会馆。1866年恭亲王奕建议在同文馆内添设算学，1868年曾国藩、李鸿章于上海江南制造局内添设翻译馆，中国数学工作者在上述部门和外国人一起翻译了一批近代数学著作。其中较重要的有李善兰与伟烈亚力翻译的《几何原本》后 9卷（1857）、《代数学》13卷(1859)、《代微积拾级》18卷(1859)；华蘅芳与英人傅兰雅合译的《代数术》25卷 (1872)、《微积溯源》8卷（1874）、《决疑数学》10卷(1880)；邹立文与狄考文编译的《形学备旨》10卷(1885)、《代数备旨》13卷(1891)；《笔算数学》3册 (1892)；谢洪赉与潘慎文合译的《代形合参》3卷(1893)，《八线备旨》4卷(1894)等等。《代微积拾级》是中国第一部微积分学译本，《代数学》是英国数学家A.德·摩根所著，是一部重要的符号代数学译本，《决疑数学》是第一部概率论译本。在这些译著中，创造了许多数学名词和术语，至今还在应用，但所用数学符号一般已被淘汰了。戊戌变法(1898)以后，各地兴办新法学校，上述一些著作便成为主要教科书。在翻译西方数学著作的同时，中国学者也进行一些研究，写出一些著作，较重要的有李善兰的《尖锥变法解》1卷、《考数根法》1卷(1872);夏鸾翔(1823～1864)的《洞方术图解》2卷(1857)、《致曲术》1卷、《致曲图解》1卷等等，都是会通中西学术思想的研究成果。
由于输入的近代数学需要一个消化吸收的过程，加上清末统治者十分腐败，在太平天国运动的冲击下，在帝国主义列强的掠夺下，焦头烂额，无暇顾及数学研究。直到1919年五四运动以后近代数学的研究才真正开始。