全连续算子(卷名：数学)
completely continuous operator
又称紧算子，是最接近于有限维空间上线性算子的一类重要算子。
在线性代数中，关于线性变换所相应的线性方程组的求解问题已被完全解决了，其主要结果是：非齐次线性方程组有惟一解，当且仅当相应的齐次方程组只有零解；如果齐次方程是退化的，那么共轭方程也是退化的，非齐次方程组可解当且仅当自由项必与共轭的齐次方程组非零解相正交，并且在可解时，还可写出它的解的一切形式（即通解）。20世纪初，在讨论第二类线性积分方程时，也得到了和线性方程组完全类似的弗雷德霍姆理论。后来，人们发现这种理论对（线性）全连续算子也是成立的。
全连续线性算子 设x为巴拿赫空间， T为x到自身的线性算子，如果对x中一切有界序列{xn}，存在子序列{x
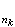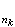)，使Tx收敛，就称T为全连续算子(或紧算子)。如果x中某子集内的每个序列都有收敛子序列，就称这个集为列紧集。全连续算子的定义可以改述为:把x中有界集映为列紧集的算子。如果对x中集M，定义M的非紧性测度为
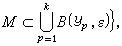式中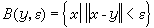
，那么全连续算子T的定义又可以改述为：对一切有界集M，满足v(TM)＝0的算子。x 上的有限秩算子（即值域是有限维的有界线性算子）就是一类重要的全连续算子。在希尔伯特空间中，每个全连续算子必为有限秩算子的一致极限（见线性算子）。这个性质在巴拿赫空间中是否成立一直为人们所注意。后来，P.恩夫洛举了一个反例，对此作了否定的回答，由此更引起人们对巴拿赫空间结构研究的兴趣。
全连续算子的另一个重要的典型例子是L2[0，1]上的积分算子：如果K(s，t)为正方形D＝{(s，t)｜0≤s，t≤1}上平方可积函数，则称由
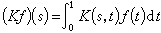确定的L2[0，1]到自身的算子K是以K(s，t)为核的积分算子，它是L2[0，1]上的全连续算子。特别，如果当s<t时，K(s，t)＝0，即有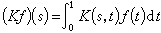，这种积分算子称为沃尔泰拉算子。巴拿赫空间x上全连续算子T有下述重要性质：①全连续算子的共轭算子是全连续算子;②T的值域不能包含无限维闭线性子空间；③对任何复数λ≠0，λI-T（I为单位算子）的值域必是闭线性子空间。
全连续算子谱分析 下面是由F.里斯和J.P.绍德尔完成的所谓巴拿赫空间上全连续算子的弗雷德霍姆理论：设T是巴拿赫空间x上的全连续算子，①当x是无限维时，零必是T的谱点，且T的谱的极限点只可能是零；②如果λ≠0是T的谱点，则它必是T的特征值，也是T
的特征值，而且T和 T相应于λ的特征子空间是两个维数相同的有限维子空间；③如果λ1，λ2，…，λn是T的任意有限个不同的特征值，x1，x2，…，xn为相应的特征向量，则x1，x2，…，xn必线性无关;④如果λ，μ分别是T，T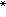的谱点，并且λ≠μ时，则T相应于λ的特征向量x与T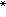相应于μ的特征向量ƒ必“正交”，即ƒ(x)=0;⑤设λ≠0，则方程(λI-T)x＝y对一切y∈x可解的充要条件是(λI-T)x=0只有零解；⑥如果λ是T的非零特征值，则方程(λI-T)x=y可解的充要条件是y与T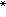相应于λ的一切特征向量ƒ正交;⑦如果λ0是T的非零特征值，则在λ0的某个邻域中，(λI-T)-1必有P.A.洛朗展开：
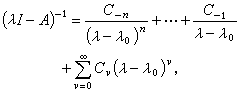式中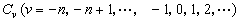
是 x上有界线性算子。迹算子 对希尔伯特空间上的全连续算子T，则进一步还可以找到两个就范正交系{en}和{φn}以及一列非负实数λn→0，使
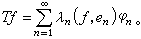称{λn｜n＝1，2…}为T的奇异数。如果奇异数满足
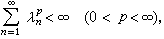就称T为σp类全连续算子，而其中σ1类算子又称为迹类算子，σ2类算子称为希尔伯特-施密特算子。对迹类算子T，它的所有特征值组成一个绝对收敛级数，称T的特征值之和为迹，记为trT。对希尔伯特－施密特算子，以它奇异数平方和的平方根作范数，也成为一个希尔伯特空间，这时内积(T，S)＝tr(S
T)。卡金代数 全连续算子类有一个重要的代数性质：在巴拿赫空间x的有界线性算子全体B(x)中，全连续算子全体H(x)是一个闭的双侧理想，即当T为全连续算子时，对任何A，B∈B(x)，ATB仍是全连续算子。在无限维空间中，单位算子不是全连续的，所以H(x)是B(x)的一个真理想。由此可以构造一个商代数B(x)/H(x)，称为卡金代数。
弗雷德霍姆算子 设π为B(x)到B(x)/H(x)的典型映射:π(A)＝A+H(x)，如果π(A)在B(x)/H(x)中可逆，就称A为弗雷德霍姆算子。这时，R(A)为闭的，且KerA和x/R(A)是有限维空间。定义A的指标
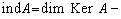
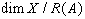，x上的弗雷德霍姆算子全体记为F(x)。A到ind A的映射是F(x)到整数群Z的连续同态，而且在紧扰动下不变，即对
，成立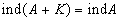
。在希尔伯特空间的情况下，若
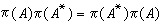，则称A为本质正常算子。对本质正常算子，利用弗雷德霍姆指标，有下面非常重要的结果。布朗－道格拉斯－菲尔莫定理 在复可分希尔伯特空间H中，T1，T2为H上本质正常算子，则存在酉算子U，使
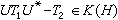的充分必要条件是
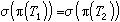，且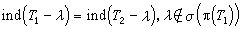
。在非线性算子理论中也可引入全连续算子，虽然它失去了上述全连续线性算子的许多重要性质，但仍是很重要的一类非线性算子。