三角级数(卷名:数学)
trigonometric series
一种特殊的正交函数级数。形如
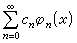 的级数称为正交函数级数,其中сn是和x无关的实数,{φn(x)}是在某固定区间[α,b]上正交的函数系,特别当正交函数系是[0,2π]上的三角函数系时,相应的级数可写作
的级数称为正交函数级数,其中сn是和x无关的实数,{φn(x)}是在某固定区间[α,b]上正交的函数系,特别当正交函数系是[0,2π]上的三角函数系时,相应的级数可写作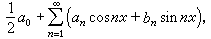 (1)称为三角级数。 式中αn(n=0,1,2,…)和bn(n=1,2,…)是与x无关的实数,称为三角级数(1)的系数。
(1)称为三角级数。 式中αn(n=0,1,2,…)和bn(n=1,2,…)是与x无关的实数,称为三角级数(1)的系数。三角级数(1)还可以写成下面复数形式的级数:
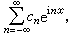 (2)式中系数
(2)式中系数 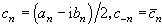 (叿n表示сn的共轭复数)。级数(2)的部分和Sn理解为
(叿n表示сn的共轭复数)。级数(2)的部分和Sn理解为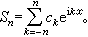
如果三角级数(1)对一切实数x都收敛,那么(1)表示了实数轴上的一个周期为2π周期函数ƒ(x),即ƒ(x+2π)=ƒ(x)对一切x∈(- ∞,∞)都成立。这是因为(1)中每一项都是周期为2π的周期函数。但是实际问题往往是,对给定的函数ƒ,如果它是具有周期2π的周期函数,需要把它表示成三角级数(1)。19世纪初,法国科学家J.-B.-J.傅里叶在研究热的流动时,为了求解热方程,首先就提出了这个想法。他的设想,虽然从现在的观点看,缺乏理论的严谨性,但却是人们对三角级数进行研究的出发点,对于近代数学以及物理、工程等许多学科都有着深远的影响。
如果三角级数(1)一致收敛于连续函数ƒ(x),那么用coskx或sinkx去乘级数(1),再在区间(0,2π)上进行积分,注意到逐项积分的可能性,就得到系数αn,bn与函数ƒ的关系式:
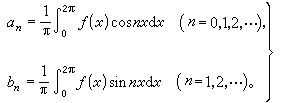 (3)公式(3)表达的系数αn,bn称为函数ƒ的傅里叶系数,以ƒ的傅里叶系数为系数的三角级数就称为ƒ的傅里叶级数。上面的事实说明:一致收敛于函数ƒ的三角级数必为ƒ的傅里叶级数。
(3)公式(3)表达的系数αn,bn称为函数ƒ的傅里叶系数,以ƒ的傅里叶系数为系数的三角级数就称为ƒ的傅里叶级数。上面的事实说明:一致收敛于函数ƒ的三角级数必为ƒ的傅里叶级数。对于给定的周期函数ƒ(x),如果ƒ是可积的,那么从(3)式仍然可以得到αn,bn,从而得到相应的傅里叶级数(1)。这就建议人们去研究ƒ 的傅里叶级数是否收敛于ƒ以及有关的许多问题。从19世纪到现在,傅里叶级数的理论逐步得到建立,已成为三角级数理论中的一个基础分支,也是一个具有广泛应用的工具学科(见傅里叶级数)。
傅里叶级数的性质,由函数ƒ可以通过(3)进行研究。自然要问,任意的三角级数(1),是否为某函数的傅里叶级数呢?这个问题的答案是否定的。因为根据傅里叶系数的性质,傅里叶系数αn,bn必须满足条件
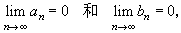 由此可知系数不趋于0的三角级数不可能是傅里叶级数,例如
由此可知系数不趋于0的三角级数不可能是傅里叶级数,例如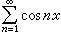 是三角级数,而不是傅里叶级数。
是三角级数,而不是傅里叶级数。那么系数αn,bn趋于0的三角级数(1),是否为傅里叶级数呢?下面的例子
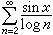 说明,它的系数趋于0,而且级数处处收敛于某函数ƒ(x),但因
说明,它的系数趋于0,而且级数处处收敛于某函数ƒ(x),但因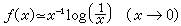 在原点附近不可积,公式(3)不成立,所以上述三角级数不可能是ƒ(x)的傅里叶级数。进一步可以证明,上述级数不可能是傅里叶级数。
在原点附近不可积,公式(3)不成立,所以上述三角级数不可能是ƒ(x)的傅里叶级数。进一步可以证明,上述级数不可能是傅里叶级数。三角级数(1)的共轭级数是
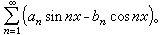 (4)(1)和(4)分别是单位圆(|z|≤1)内幂级数
(4)(1)和(4)分别是单位圆(|z|≤1)内幂级数 (5)当z=eix(x为实数,i为虚单位)时的实部和虚部。所以三角级数(1)和它的共轭级数(4)的性质正好反映了幂级数(5)表示的解析函数在单位圆边界附近的性质。
(5)当z=eix(x为实数,i为虚单位)时的实部和虚部。所以三角级数(1)和它的共轭级数(4)的性质正好反映了幂级数(5)表示的解析函数在单位圆边界附近的性质。值得注意的是,傅里叶级数的共轭级数未必是傅里叶级数。例如,级数
 是傅里叶级数,而它的共轭级数
是傅里叶级数,而它的共轭级数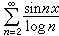 却不是傅里叶级数。但是可以证明,如果级数(1)是某函数ƒ的傅里叶级数,并且|ƒ|p是可积的,其中p>1,那么它的共轭级数(4)也是傅里叶级数。
却不是傅里叶级数。但是可以证明,如果级数(1)是某函数ƒ的傅里叶级数,并且|ƒ|p是可积的,其中p>1,那么它的共轭级数(4)也是傅里叶级数。一般的三角级数,由于不存在关系式(3),因此增加了它的复杂性。到目前为止,人们对它的了解还是十分初步的。值得注意的是,三角级数往往可以提供许多奇特的函数,这对数学理论的基础研究,有着重大的意义。
例如,用所谓F.里斯的无穷乘积
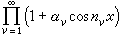 (6)逐项乘得的三角级数,只要正整数nυ满足条件
(6)逐项乘得的三角级数,只要正整数nυ满足条件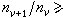
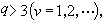 且系数
且系数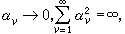 那么(6)乘得的三角级数几乎处处收敛于0,而它的系数却不全为0。
那么(6)乘得的三角级数几乎处处收敛于0,而它的系数却不全为0。又例如缺项很多的三角级数
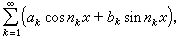 (7)当它的缺项满足条件
(7)当它的缺项满足条件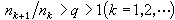 时,称为阿达马缺项三角级数。它具有很奇特的性质:要么几乎处处收敛于一个平方可积函数,要么几乎处处不收敛,如属后者,则它不是傅里叶级数。
时,称为阿达马缺项三角级数。它具有很奇特的性质:要么几乎处处收敛于一个平方可积函数,要么几乎处处不收敛,如属后者,则它不是傅里叶级数。中国在三角级数方面开展研究最早的是陈建功。他从1928年开始就在日本《东京皇家科学院学报》发表关于正交函数级数的文章,他于1930年在日本岩波书店出版的《三角级数论》是国际上三角级数论方面较早的专著之一。