抽样(卷名：现代医学)
sampling
从研究对象的全体（统计学上称为总体）中随机抽取一部分(统计学上称为样本)进行研究，并据以论断总体特征的统计学方法。在医学中广泛采用。例如，为了制订中国少年儿童生长发育时身体的正常值，中国3亿少年儿童就是研究的总体，在用抽样方法进行研究时，只需从总体中抽取一个样本(如10万人)进行身体测量，最后以此10万人的测量结果来推论全国少年儿童身体生长发育的正常值。用样本来推论总体是有条件的，并不是从总体中抽取的任何一部分样本都可用来推论总体，只有在解决了样本的代表性、可比性的前提下，掌握了抽样误差的大小及发生概率时，才能用样本来推论总体。此即抽样研究中的四性（代表性、可靠性、可比性、显著性）。
样本的代表性 一个有代表性的样本，必须是总体的一个具体而微的缩影，也就是说，样本除了比总体小以外，在组成、变异等特征方面，均应与总体相同。上例中，中国的3亿少年儿童是由地理区域、民族、家庭经济状况、文化背景各不相同的少年儿童组成。从中抽取的10万人的样本，也必须包括地理区域、民族、家庭经济状况、文化背景各不相同的少年儿童，而且各特征的内部构成必须与总体基本一致。如果只抽南方儿童，某个测量指标将偏低，如果只抽北方儿童，此测量指标必然偏高。又如，欲了解某药对急性细菌性痢疾的疗效，如果只抽取在传染病院住院的急性菌痢病人为样本，那么它对总体来说就没有代表性，因为急性菌痢有轻有重，而病情的轻重是影响疗效的重要因素，住院者多为重症，故其疗效实际是对重症急性菌痢的疗效，而不能代表全部急性菌痢的疗效。为了保证样本具有代表性，首先要对研究的总体有十分明确的认识，例如，为了研究某药对细菌性痢疾的疗效，研究总体就应包括急性、慢性、不同年龄不同病情不同菌型的患者的全体。具有代表性的样本就必须包括上述各种类型的病人。又如为了研究某药对儿童急性普通型菌痢的疗效，则研究总体就是15岁以下，不合并中毒性休克的急性菌痢患者的全体。此时抽样只需包括15岁以下，无中毒性休克的急性菌痢病人。上述第一种情况中，总体范围太大，样本数量必然很大，而实际工作中，往往不能达到如此大的样本。后一种情况中，由于总体范围较小，抽样容易得多，但其结论也只能推论14岁以下普通型急性菌痢的疗效，而不能推广至各种类型的菌痢患者。另外，当研究总体不够明确、具体时，往往易导致系统误差。例如，要研究3岁儿童的身高，就必须明确规定出生年月的范围（如1986年满 3周岁的儿童应为1983年1月1日至1983年12月31日出生的儿童），否则由于各地计算年龄的方法不同，则很可能将不到3岁的孩子误抽为样本，这样必然影响研究结果的准确性。
为了保证样本具有代表性，抽样时还应当遵守随机的原则，即要保证总体中，每个个体都有同等机会被抽到。例如，要在某工厂内观察某中药对某病的疗效，除对影响该病的因素（如病程、病情等）要作明确具体的规定外，还要使在规定范围内的全体病人中，每个人都有同等的被抽取为观察对象的机会。如可按病人的工作证号编码抽样，也可按车间班组抽样，而不能由医务室提供受试者名单，因为这样提供的名单往往是病程长、病情重或经其他药物治疗无效者的名单。同样，也不能让患者自愿报名受试。因为一般中药服用较麻烦，且味苦，故多数患者往往先选择服用简便的药物，如果让患者自愿报名，则多数受试者，必然是疗程过长或其他药物治疗无效者。
样本的可靠性 一个有代表性的样本，不一定就可以用来推论总体，这是因为从有变异的总体中抽取样本，即使遵循了随机化的原则，偶然的抽样机遇也会使样本与总体之间有一定的差异。例如，在某地正常成年人的总体中，随机抽取1000人，测定血清谷氨酸－丙氨酸转氨酶(GPT)的平均值为85单位。在同样条件下(抽样方法、检测技术、仪器试药均相同)再抽取1000人进行测定，则平均值不一定仍是85单位，而可能是75、80或90单位等。如果由于偶然的机会，多抽取了一些GPT高的人，所得平均值就偏高。多抽取了一些 GPT低的人，平均值就偏低。这种偶然的抽样机会导致的误差，在统计学上称为抽样误差。抽样误差在抽样调查中客观存在，不可避免。因此，在用样本推论总体时，必须考虑抽样误差的大小及其发生规律，从而借此确定用样本推论总体的可信程度。
标准误 用来表示抽样误差大小的指标，实际是均数的标准差（见平均数、变异度）。在统计学中标准差是反映事物变异程度的指标。例如20岁左右女青年的身高可以1.5米至1.9米，但若分别测量两组同年龄的女青年（宾馆服务员和大学生）的身高并计算其标准差，则结果必然是大学生组的标准差大于宾馆服务员组。这是因为招收宾馆服务员时身高有一定的要求，过矮过高的都不录取，故她们的身高变异程度小，或者说身高较整齐；而大学生的身高并非录取条件，故她们的身高参差不齐，或者说变异程度大。设有一研究总体，总体均数为 μ，在此总体中，多次重复抽样，每次抽样均可得到一个样本均数，这些样本均数必然有的比 μ大，有的比μ 小；有的距离μ 较近，有的距离μ 很远。这些样本均数也有一个变异程度，用来表示这种变异程度的指标就是均数的标准差，或称为标准误。
测量资料（平均数）的标准误的计算公式为
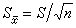式中S塣为标准误，S为标准差，n为样本数。计数资料（比例数）的标准误计算公式为
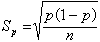式中Sp为比例数的标准误，p为样本的比例数（如治愈率等），n为样本数。由以上计算公式可以看出：标准误（抽样误差）的大小与该事物的变异程度成正比（从变异大的总体中抽样，抽样误差大，反之抽样误差小），与样本数的平方根成反比（样本数愈大，抽样误差愈小）。
可信限 也称可信区间。样本统计值与总体统计值之间，由于偶然的抽样机遇总会存在一定的差异。因此，用样本推论总体时，只能推论总体所在的范围，及在此范围内的概率，而不可能确切推论总体的统计值。这种用样本推论总体所在的范围，即称为可信限，常用的有95％及99％的可信限。以下简述其原理及计算方法。
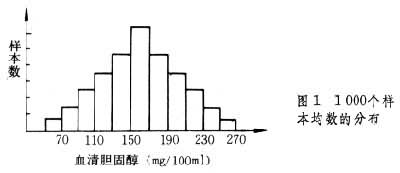
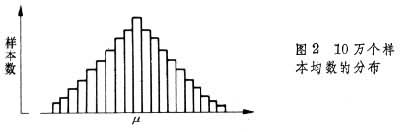
假设某地区全部正常成年人的血清胆固醇的总平均值为160mg/100ml，在此总体内重复抽样1000次，则可得1000个样本均数。可以看到这些样本均数有的比 160大，有的比160小，但与160接近的最多，距离160往两端愈远的愈少。如果把这些样本均数的分布用直方图表示，即可得图1。图中横轴为均数的组段（血清胆固醇），纵轴为样本数。若抽样次数再增加，组再分细，则可得图2。当抽样次数增加到无限多，直方图的锯齿消失，成为一条光滑的曲线，即图3，此曲线与统计学中的正态曲线极为近似。因此可以借用正态曲线的规律来推论总体所在的范围。
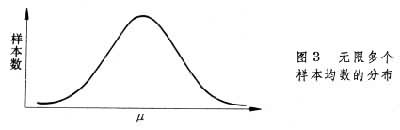
正态曲线 以总体均数为中心（最高点），往两端逐渐降低但与横轴永不相交，两侧完全对称的钟形曲线（图 4）。若以此曲线下的总面积为100％，以μ 表示总体均数，σ塣表示总体标准误，则曲线下各部分的面积有如下分布规律：
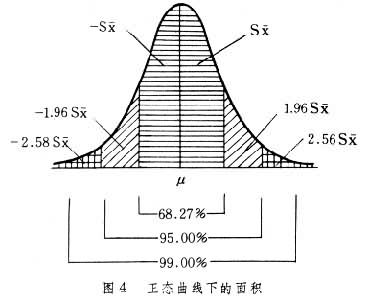
μ±σ塣的面积占曲线下总面积的68.27％
μ±1.96σ塣的面积占曲线下总面积的95.00％
μ±2.58σ塣的面积占曲线下总面积的99.00％总体标准误 σ塣 是说明样本均数围绕总体均数变异程度的指标，在实际工作中常用样本标准误S塣来代替。μ±S塣的面积占总面积的68％的含义是：若从同一总体中重复抽取100个样本，则这100个样本均数有68个在 μ±S塣的范围内，比 μ－S塣小的和比μ＋S塣大的样本均数各有16个。换一个角度来说，68％就是一个样本均数落在μ－S塣至 μ＋S塣范围内的概率。
同理， μ±1.96S塣的面积占总面积的95％，这说明一个样本均数落在 μ－1.96S塣至μ＋1.96S塣范围内的可能性是95％，而比 μ－1.96S塣小的和比μ＋1.96S塣大的可能性各有2.5％。μ±2.58S塣的面积，占总面积的99％，这说明一个样本均数落在 μ－2.58S塣至μ＋2.58S塣范围内的可能性是99％，在此范围以外的可能性只有1％。
以上规律是样本均数(塢)，距离总体均数(μ)的规律，但也可把它视为总体均数离开样本均数的规律，因为在实际工作中，可以得到的是样本均数，要推论的是总体均数。既然样本均数与总体均数相差±S塣的概率是68％，相差±1.96S塣的概率是95％；那么总体均数与样本均数相差±S塣的概率当然也是68％，总体均数与样本均数相差 ±1.96S塣的概率也是95％ 。因此所谓 塢±1.96S塣即95％的可信限。它的含意是:总体均数在塢±1.96S塣范围内的概率是95％。或者说总体均数在 塢±1.96S塣范围内的可信程度是95％。所谓塢±2.58S塣即99％的可信限，它的含意是，总体均数在 塢±2.58S塣范围内的概率是99％，或者说总体均数在 塢±2.58S塣范围内的可信程度为99％。
例如，为了了解某地正常成年人血清胆固醇的平均值，随机抽取500人，测得样本均值塢＝165.0mg/100ml，标准差S=52.0mg/ml，并由n=500求得S塣＝2.33mg/100ml;则95％的可信限为：165±1.96×2.33，即160.43～169.57mg/100ml。这说明该地区正常成年人血清胆固醇的平均值在160.43～169.57mg/100ml范围内的概率为95％。
样本的可比性 在医学研究中，常常需要判断某种治疗或预防措施的效果；也常需要分析研究影响疾病发生及转归的因素。在解决这两类问题时，往往要同时抽取两个或两个以上的样本进行对比分析，因为许多疾病可能自愈或自然缓解，没有对比分析就很难下结论。例如，有人用柳树叶治疗急性黄疸型肝炎（以下简称急黄肝）120例，10周后基本治愈者93例，治愈率为 77.5％。于是下结论：“柳叶治疗急黄肝疗效好”。这样的结论是不科学的。实际上，急黄肝只要注意休息、营养，不给任何特殊治疗，10周后也必然会有一部分人自愈。如有人曾对与上述病人相同的70例急黄肝进行观察，除维生素B、C及酵母外，不给其他任何药物，10周后基本治愈的49例，治愈率70％，这说明急黄肝不给特殊治疗，也有70％自愈，所谓77.5％的柳树叶疗效实际上是虚假的。
在对比分析研究时，最重要的前提是对比组之间必须具有可比性。样本间的可比性指相互比较的样本之间，除了要比较的因素（如不同药物）以外，其他影响研究结果的主要因素要控制得基本相同。例如，要比较不同治疗方法对高血压病的疗效时，比较组间除治疗方法不同以外，其他影响治疗效果的主要因素，如病情、病人的年龄等均应控制得基本相同。
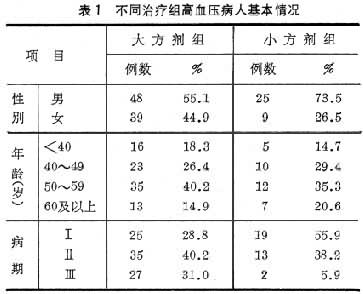
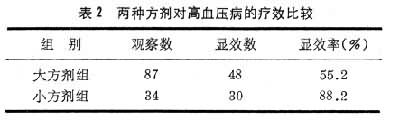
表1、表2为不同方剂对高血压病疗效的资料。不能根据表2就得出结论:小方剂的疗效比大方剂好，因为从表1可以看出两组病人的病情相差很大。大方剂组中Ⅰ期病人占28.8％，其余为Ⅱ、Ⅲ期病人;而小方剂组中Ⅰ期病人占55.9％，其余为Ⅱ、Ⅲ期病人。这说明大方剂组病人病情重得多。这组病人的疗效不好是因为治疗方法不好（方剂过大）还是病情较重，据此资料是不能断定的。
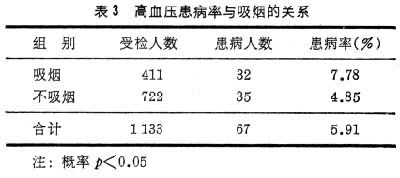
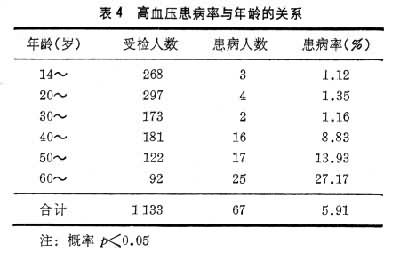
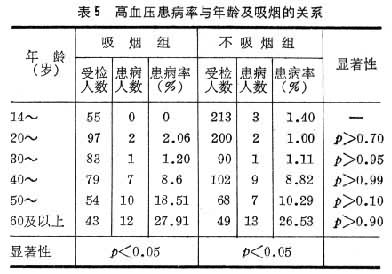
控制样本间的可比性，实际是去除混杂因素的干扰。表3、表4为高血压流行学调查报告的资料。研究者分析了高血压的患病率与吸烟和年龄的关系，经显著性检验后，认为这两个因素均影响高血压的患病率。两个表的观察总数均为1133，但表 3在吸烟组与不吸烟组中，并未控制年龄基本相同；而表4未控制各年龄组中，吸烟者的比重基本一致，故上述结论是站不住脚的。正确的做法应该将两个因素放在一起来考虑，如表5所示，表中纵向看为吸烟的和不吸烟的不同年龄组的患病率；横向看则为在同一年龄组中(即控制年龄相同)吸烟者和不吸烟者的患病率。表5表明高血压的患病率与病人的年龄有关(随年龄升高而升高)，而与吸烟无关。应该指出表5这样的组合表的分析，只适用于因素较少的情况（一般3～4个因素）。因素过多时，分组过多，每个格子内的数据就少，而样本往往达不到足够分析的数量，因素较多时，一般用多元分析的方法处理（见多变量统计分析）。
样本的显著性 若同时抽取多个样本进行研究，则同样也存在抽样误差问题。大量实践证明，黄连素治疗急性普通型细菌性痢疾的疗效为90％。设某中草药治疗同类痢疾的总有效率为70％。若从黄连素治疗的急性菌痢总体中抽样，由于抽样机遇完全可能得到p1及p2的样本（图5），当然，也可以得到其他数值的样本。同理，在用中草药治疗的急性菌痢总体中抽样，也完全可能得到p3及p4的样本。p1和p2来自同一总体，它们之间有10％的差异，这是由于抽样的偶然机遇所致。p1与p3之间也有10％的差异，但它们来自不同的总体，这种差异是本质因素（本例为治疗药物不同）不同所致。由此可见：当两样本（或多样本）间有差异时，其来源有两种可能性，一是两样本间本来没有什么差异，它们来自同一总体，它们之间的差异是偶然的抽样机遇所致，是没有意义的；另一种情况是两样本来自本质不同的两个总体，它们之间的差异不能用偶然的抽样机遇来解释，是有意义的。统计学中的显著性检验，即用以检验这两类差异中，哪一类发生的可能性大。显著性检验的方法很多，但无论哪一种方法，其基本原理都是先假设两样本来自同一总体，即先假设两样本之间的差异是偶然的抽样机遇所致，是没有意义的（这一假设在统计学上，称为检验假设或无效假设）。然后根据一定的公式计算，获得两样本之差由偶然的抽样机遇所致的概率p值。若p值大，说明两样本之间的差异由偶然的抽样机遇所致的机会大，符合原假设，不能推翻原假设，也即两样本之间，无本质差别，或差异无意义（无显著性）。若p值小，说明两样本之间的差异由偶然的抽样机遇所致的机会小，故可以推翻原假设，也即两样本之间的差异是由某些本质因素不同所致，是有意义的（有显著性）。统计学上人为规定显著性的界限如下:p≤0.05为有显著性，p>0.05为无显著性，p≤0.01为有极(高度)显著性。应当强调的是，p值的大小与样本间差异的大小是两回事，p值说明的是样本间的差异由偶然抽样机遇所致的概率大小，而不是样本间的差异大小。另外，只有在样本具有可比性的前提下，进行显著性检验才有意义，否则p值再小，也不能反映样本间的差异有意义。
