地球流体力学(卷名：力学)
geophysical fluid dynamics
━━━━━━━━━━━━━━━━━━━━━━━━
学科的形成
研究方法
研究内容
基本方程
拉普拉斯潮汐方程组
斜压原始方程组
位涡量守恒方程
基本无量纲参数
罗斯比数RO
埃克曼数Ek
运动的分类
重力－惯性波
行星波
埃克曼流
大气环流
大洋环流
准地转运动
非地转运动
基本动力过程
地转适应过程
准地转演变过程
准地转模式
应用和发展趋势
━━━━━━━━━━━━━━━━━━━━━━━━
流体力学的一个分支，研究地球以及其他星体上的自然界流体的宏观运动，着重探讨其中大尺度运动的一般规律。它是 20世纪 60年代发展起来的一个新学科。geophysical fluid dynamics按字义为“地球物理流体力学”，由于考虑到地球和自然界还有包含化学反应的许多流动过程也日渐成为这一学科的研究内容，故以译作地球流体力学为宜。另外，这个学科在国际上还有一些别的名称，其中一个比较流行的是“自然流体力学”(natural fluid dynamics)。
学 科 的 形 成
近百年来，人类对天气预报、航海和海洋资源开发的需要不断增长，大气大尺度运动和海洋大尺度运动的研究得到了发展，逐渐形成了大气动力学和海洋动力学。随着空间科学技术的发展，研究近地空间和其他星体的流体运动已成为现实，而随着地质和地球物理学的发展，研究地幔运动也成为重要的课题。流体力学的一般原理虽然也适用于上述自然界流体运动，但像天气系统和大洋环流等流体运动是由自然界中巨大的能源所推动，其时间尺度和空间尺度都比气体动力学和水动力学（见液体动力学）等与生产技术有关的流体运动的尺度要大得多，而引力、星体的自旋以及能量的交换和转移过程又在其中起着主要作用，因而这些流动具有非常鲜明的特点和共同的基本规律。研究这些共同的基本规律能使人类对大气或海洋等各种具体运动的特点和规律有深刻的认识。地球流体力学正是在这种背景下逐渐形成的。
研 究 方 法
地球流体力学同大气动力学或海洋动力学之间并无明确的界限。一般说，地球流体力学研究的对象较广并侧重一般规律，主要任务是建立由自然界流体运动抽象出来的模式和研究如何抽象的方法。而对大气运动和海洋运动的具体形态的研究则分别属于大气动力学和海洋动力学的范围。
地球流体力学的研究方法有理论分析法、模拟实验法和数值试验法。理论分析法是通用的。模拟实验法对研究地球流体运动的机理很有用，但难于在实验室中复制大气运动和海洋运动，因为不可能同时满足众多的相似条件。数值试验法起着愈来愈重要的作用，因为自然界流体运动中各种现象往往同时并存，起作用的因子很多，机制极其复杂，非做数值计算难于得到较精确的结果。此外，实地观测虽也是认识自然界流体运动的基本方法，但它属于气象学和海洋学的范围，不包括在地球流体力学之中。
研 究 内 容
地球流体力学目前主要通过建立有关模式来研究大气和海洋大尺度运动，并且研究支配这些运动的基本方程、基本运动形态和基本动力学过程。
基本方程 一般的流体力学基本方程组也适用于地球流体力学，但须考虑具体条件进行适当的修改。
拉普拉斯潮汐方程组 P.-S.拉普拉斯最早用流体动力学观点研究海洋潮汐所使用的偏微分方程组，也是地球流体力学的基本方程组。
设在半径为α的球面上覆盖着密度为ρ的均质流体，自由表面高度为h，其平均值为媢；并设流体在垂直方向是静力平衡的，只有水平方向的运动而且是上下均匀的。这样，流体力学基本方程组中的运动方程可简化为两个标量方程，而连续性方程则化成一个描写自由表面高度随时间变化的方程，即
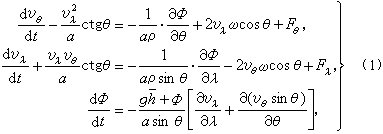式中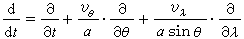
；ф＝g(h-媢);g和 ω分别为地球重力加速度和地球自转角速度；θ、λ为余纬和经度;vθ、vλ为流体质点相对运动的速度分量;Fθ、Fλ为外力分量，研究潮汐时即为引潮力分量。上述方程组称为非线性潮汐方程组，又称正压原始方程组;略去其非线性项即得拉普拉斯潮汐方程组。它从本质上说明潮汐是由引潮力引起的波动。因它过于简单，而海底和海岸又是很复杂的，不能用此方程作实际的潮汐计算。但它是描写流体在重力和科里奥利力（见相对运动）作用下运动状况的基本方程组，在推广为三维问题时，还可以解释大气中（尤其是平流层以上高空）的大气潮汐现象（太阳辐射作用激发出来的大气日变化）。斜压原始方程组 描述大气和海洋三维大尺度运动的基本方程组。通过它可以研究外界能流对自然界流体运动的影响。对水平尺度远大于垂直尺度的运动，可略去运动方程的垂直加速度，使垂直方向的运动方程变为静力平衡方程；再补上连续性方程、热力学第一定律和状态方程即得斜压原始方程组。此外，由于大气中的水汽相变过程和海洋中的盐分循环过程很重要，常常还要将和这些过程相应的方程补充进去。斜压原始方程组是基本的，但很复杂，故在理论研究中还需进一步简化。
位涡量守恒方程 由正压原始方程组 (1)导出的一个方程，说明在理想流体中每个质点的位涡量守恒（不随时间变化）。该方程比原始方程组更便于作理论研究。由正压原始方程组(1)可定义出位涡量
Ωp＝ф
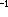(Ω＋2ωcosθ)，式中
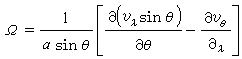为流体相对运动的涡量的垂直分量。当 Fθ=Fλ=0时，就有位涡量守恒方程dΩp/dt=0。对理想斜压气体，有位涡量Ωp=ρ-1墷s·(Ω+2ω)和位涡量守恒方程dΩp/dt=0，式中s为气体质点的熵；墷为梯度算符；Ω和ω分别为相对运动的涡量和坐标系自转角速度。用不同的简化基本方程，位涡量的形式也稍有不同。例如，若自由表面的平均高度很大，而变化很小，则在正压原始方程组中可用(g媢)-1(Ω+2ωcosθ)代替位涡量Ωp，于是得到绝对涡量2ωcosθ＋Ω 守恒。
基本无量纲参数 将运动方程中各种力的特征量与科里奥利力的特征量相比就得到地球流体力学中所特有的各种无量纲参数。最重要的有罗斯比数和埃克曼数等。
罗斯比数RO 惯性力与科里奥利力之比的特征数，芝加哥气象学派为纪念其创立者 C.-G.A.罗斯比而取此名。但此参数实由气象学家И.А.基别尔最先引进，故又常称罗斯比－基别尔数。设运动的特征水平尺度和特征水平流速分别为L和U，记科里奥利参数 2ωcosθ为f，并设惯性力的特征量由平流项(如vθдvλ/aдθ)所决定，则有RO=U／fL。RO《1说明科里奥利力支配着运动的特性，此时基本方程组可大为简化。
埃克曼数Ek 耗散力与科里奥利力之比的特征数，为纪念海洋学家V. W. 埃克曼而命名。设耗散力主要由
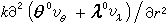决定，则有Ek=k/fD2式中k为耗散系数；r为半径（或垂直高度）；D为运动在垂直方向的特征长度；θ0和λ0为单位矢量。在靠近地球表面或别的行星固体表面的厚度为Dθ＝
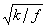的流体层内有 Ek≈1，耗散力和科里奥利力同等重要，形成行星边界层。运动的分类 地球流体运动按空间尺度或性质可分为下列数种类型：重力－惯性波、行星波、埃克曼流、大气和大洋环流、涡旋、重力波和对流等。后三者为一般流体力学所共有，这里不单独解释。
重力－惯性波 地球流体的一种基本运动形式，由重力和科里奥利力共同作用所形成。相速常远大于流速。若波长较短，则科里奥利力影响极小，它与通常分层流动中的重力波无异。但若波长较长，特别是波长和地球（或别的行星）同量级时，科里奥利力影响明显，则波的相速和结构都和重力波有明显的不同。
行星波 地球的大气运动、海洋运动及其他行星大气大尺度运动最明显和最重要的形式，流场弯曲如波状，波长大都与行星半径同量级（在洋流中波长较短），因而得名。罗斯比在研究大气运动时和H.阿尔文在研究太阳流体运动时都强调这种波，因而它常被称为罗斯比-阿尔文波或罗斯比波。行星波与大型天气系统有密切关系，又是大气环流或大洋环流的主要组成部分，故为大气动力学、海洋动力学和地球流体力学的主要研究对象。行星波相速和流速同量级，涡量远大于散度，故又称为涡旋波。事实上，若ω=0，和式(1)相应的线性方程除有重力波解外，还有定常的涡旋场解。若ω厵0，则涡旋场为非定常，成为涡旋波；且忽略二维可压缩性（取二维散度为零）时，它也存在；能量来源于流体运动自身的惯性，故又称为惯性波。
埃克曼流 行星边界层内的流动，由埃克曼首先阐明，故名。亦常称为行星边界层流。其主要特征是流体速度水平分量沿高度呈螺线变化，称为埃克曼螺线。埃克曼流常诱发垂直速度，称埃克曼抽吸，影响行星边界层外的大尺度运动。
大气环流 大气中各种大尺度运动的全体组成的具有最大空间尺度的运动。现已发现两种非常不同的大气环流型。
① 罗斯比环流型 由明显的行星波组成的非轴对称的大气环流型，为纪念阐明行星波的罗斯比而命名。地球大气环流即属此型。
② 哈得莱环流型 大气环流表现为对星体自旋轴对称和准对称的大气环流型。由G.哈得莱首先阐明，故名。木星大气环流即属此型。
大气环流型主要取决于星体自转角速度 ω以及星体大气受太阳辐射而造成极地和赤道之间的温差|ΔT|。若大气加热呈轴对称分布而星体不自转，则热量交换取纯对流形式，即热气反抗重力作用而上升，冷气下沉且从底层流向暖区，此即纯哈得莱环流型。但若星体自转，则在科里奥利力作用下，大气运动中沿子午圈的速度分量vθ产生沿纬圈上的速度分量vλ。ω和|vθ|愈大，则|vλ|愈大。大到一定程度后，由这种轴对称运动所导致的热量沿子午圈的流量过小，积集起来的热量由非轴对称的水平方向的运动来输送，形成明显的行星波，大气环流变为罗斯比环流型。故当 ω和|ΔT|为中等大小时，大气环流为罗斯比环流型。但若|ΔT|固定而 ω增到一定程度，或ω固定而|ΔT|增加过大，则|vλ|过大，轴对称环流又占主要地位，转变为哈得莱环流型。人类经历了两百多年的研究，特别是最近三十年通过旋转圆盘内流体运动的模拟实验以及相应的理论分析才最后弄清上述机理，这对认识大气环流的本质有很重要的意义。
若大气环流为罗斯比环流型，则在一些纬度带内，暖气下沉，冷气上升，和哈得莱环流型的情况相反。这些地带的子午圈环流称为反哈得莱环流。地球大气在中纬度地区即属此情况。
大洋环流 地球上海洋中各种大尺度运动的全体组成的最大空间尺度的运动。大洋环流和大气环流有许多共性，但海岸的几何约束对洋流有明显的影响，使大洋环流具有特点。最简单的一种大洋环流模式是惯性洋流，它具有地球上大洋环流的主要特征。在这种模式中，有定常的风应力作用于洋面上，风应力、科里奥利力和惯性力三者相平衡。在开阔洋面上洋流为风应力所驱动，然后受惯性力作用流向海岸地带，科里奥利力随纬度的变化使向西流动的洋流加速，称西向强化现象；子午线走向的海岸的几何约束，使洋流转向流向高纬地区并强化（北向强化现象）。这是大西洋弯流和太平洋暖流的显著特点。
地球流体运动也常按科里奥利力影响的程度分为准地转运动（quasigeostrophic motion）和非地转运动(ageostrophic motion)两大类：
准地转运动 满足RO《1和Ek《1的运动。在这类运动中，重力、压强梯度力和科里奥利力三者几乎平衡，且运动为准水平的，沿重力方向的速度分量很小。大气和海洋环流、行星波以及大尺度涡旋属于准地转运动，是地球流体大尺度运动的主要类型。
非地转运动 除准地转运动面外的地球流体运动。在这类运动中，重力、压强梯度力和科里奥利力三者不处于几乎平衡状态。在自由流体中RO《1不成立。重力-惯性波、重力波、对流、尺度较小的强涡旋和埃克曼流属于非地转运动。
基本动力过程 支配地球流体大尺度运动的动力过程有地转适应过程(geostrophic adjustment)和准地转演变过程(quasigeostrophic evolution)等。
地转适应过程 使地球流体非地转运动很快地调整为准地转运动的动力过程。若局部地区有非地转运动，则重力波和重力- 惯性波的能量很快地沿水平和垂直方向弥散，而科里奥利力作用则使运动较快地变为准地转运动。这就是地转适应过程的实质，也是使地球流体大尺度运动经常保持为准地转运动的重要机理。
准地转演变过程 准地转运动随时间变化的动力过程。控制此过程的因子是涡量或位涡量沿空间分布的不均匀、能源和耗散力。大气动力学、海洋动力学和地球流体力学着重研究准地转演变过程。所谓天气形势预报就是预报天气系统（大尺度大气流场）随时间的变化。
准地转模式 描写准地转运动的动力学的理论模式称准地转模式(quasigeostrophic model)。在数学上它用一个只含有流函数的偏微分方程描写，这个方程也常被称为准地转模式。引入流函数，并将速度场、温度场和压强场等按罗斯比数展开，代入位涡量守恒方程，只取零级近似，即得准地转模式。还可再引入一些小的近似，例如，用直角坐标(x，y)代替球坐标(λ，θ)，并近似地用线性关系f0+βy来代替f＝2ωcosθ，由式(1)得到正压准地转模式如下：
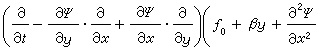
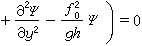， (2)式中Ψ为流函数。最常用的斜压准地转模式为：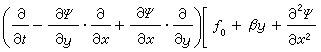 
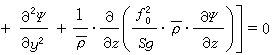， (3)孒(z)为平均情况下密度随高度的分布；
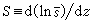称为层结参数，埅为平均情况下熵随高度的分布。在地球流体力学中，准地转模式研究得最多，应用也最广，迄今为止有关自然界大尺度运动的重要结论大都由此得出。
应用和发展趋势
近二十年来，地球流体力学的发展已促成大气动力学和海洋动力学的统一化，使这两个学科日渐成为具有严格理论基础的科学。近十年来，地球流体力学主要研究海洋动力学提出来的问题，对后者的促进尤为显著，并在海洋开发工程中得到直接应用。地球流体力学的发展趋势，一是更加理论化，且研究内容进一步扩大到包括自然界中一切受自然力作用的流体运动；二是研究更多的实用问题，例如天气和气候预报、洋流和渔汛预报、海洋运动对海洋和海岸工程影响等问题。而对特有的计算方法的研究则有可能发展成为计算地球流体力学。
参考书目
D.Fultz， Development in Controlled Experiment on Large-scale Geophysical Problems， Advances in Geophysics， Vo1.7，pp.1～103， 1961.
H.P.Greenspan，The Theory of Rotating Fluids，Cambridge Univ.Press，Cambridge，1969.J.Pedlosky，Geophysical Fluid Dynamics，Springer-Verlag， New York， 1979.
曾庆存著：大气动力学的一些问题，《力学进展》，第10卷，第1期，1980。