拉普拉斯变换(卷名：数学)
Laplace transform
一种特殊的积分变换，是狄利克雷级数到积分的推广。从已知一般可取复值的函数ƒ(t) (0≤t<+∞)，用下式定义的函数（如果下式中积分存在）
(1)称为ƒ(t) 的拉普拉斯变换，或简称拉氏变换，式中s=σ+iτ可以是复数，ƒ(t)称为原像函数，F(s)称为其像函数。为了强调F(s)是从ƒ(t)经(1)式变换得来，也常记F=Lƒ。
在一定条件下，从式(1)可以解出ƒ(t)：
(2)式中积分是沿着无穷长直线Res=σ进行的。式(2)称为拉氏反变换，记作ƒ=L-1F。式(1)与式(2)称为一对互为反演的公式，其成立有各种的充分条件。例如，设式(1)对于任何σ(=Res)>σ0绝对收敛（或在勒贝格意义下可积），这里σ0为某常数，且ƒ(t)在任何有限区间内是有界变差的，则式(2)对任何σ>σ0成立，但已假定ƒ(t)规范化，即
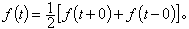
容易看出，如果(1)对于s0=σ0+iτ0收敛，则对一切s=σ+iτ，只要σ>σ0，它也收敛。因此F(s)在这里是解析的，亦即，存在一个收敛横坐标σc，使得F(s)在半平面Res>σc中解析（除非σc=+∞）。这时，有以下求导公式
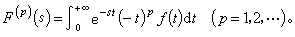若满足反演条件，这时有
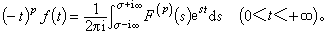换句话说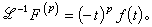
这样，拉氏反变换就把像函数的求导运算变成了原像函数和(-t)p的乘积运算。拉氏变换还有所谓卷积公式，把
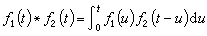叫做ƒ1，ƒ2的卷积，且F1=Lƒ1，F2=Lƒ2。这时有F1·F2=L(ƒ1*ƒ2)。
关于ƒp(t)的拉氏变换，由分部积分法（在一定条件下）可得
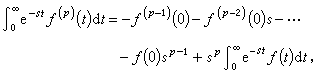即
因此，ƒ(t)的常系数线性微分方程的初值问题就可化为有关L(ƒ)的代数方程问题，而后者是极容易求解的。求出L(ƒ)后，再利用拉氏反变换公式(2)，便可求得ƒ本身。这样，拉氏变换就成为求解常微分方程的一个有力工具。同样道理，用拉氏变换的方法，可以把含两个自变量的偏微分方程化为常微分方程，或一般，把含n个自变量的偏微分方程化为含n-1个自变量的偏微分方程，使问题得以简化。以上说的是单边拉氏变换，还有所谓双边拉氏变换
(3)在一定条件下，有反演公式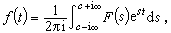
(4)式中с=Res取在使(3)绝对收敛之处。此外，还可以在不同空间，例如l2(0，∞)内考虑拉氏变换。此时积分的收敛也就要在相应的极限意义下来理解，也有相应的一系列理论。另外，还可考虑更一般的拉普拉斯－斯蒂尔杰斯变换
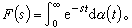(5)拉氏变换概念还可推广到广义函数上。例如，对于著名的δ函数，可定义其拉氏变换为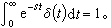
拉氏变换的理论可从傅里叶变换转化而来。
几个简单的函数的拉氏变换见表
。参考书目
河田龙夫著，钱瑞壮译：《富里哀变换与拉普拉斯变换》，上海科学技术出版社，上海，1961。(河田龍夫著：《Fourier变换とLaplace变换》，岩波，東京，1957。)
窦志著，张义良译:《拉普拉斯变换的理论和应用导论》，科学出版社，北京，1966。(G.Doetsch，Einf╇hrung in Theorie und Anwendung der laplace-TransforMati-on，Birkhuser Verlag，Basel und Stuttgart，1958.)
D.V.Widder，The laplace Transform，PrincetonUniv.Press， Princeton， 1941.
D.V.Widder，An Introduction to Transform Theory，Academic Press， New York， 1971.
G.Doetsch，Handbuch der laplace-TransforMation，Vol.1～3， Birkhuser， Basel， 1955， 1956.