平面(卷名：数学)
plane
构成几何图形的基本元素之一。在建立了空间直角坐标系Oxyz并在其上建立了坐标向量后，设n{A，B，C}为通过定点M0(x0，y0，z0)的平面π的垂直向量；点M0的向径为r0；平面π内任意点M(x， y，z)的向径为r(图1
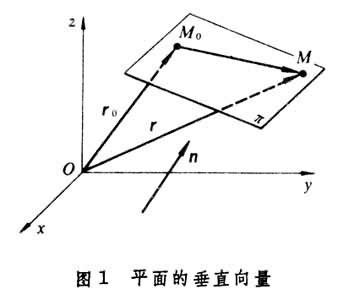)，那么平面π的向量方程为n·(r-r0)＝0，化为普通方程，为
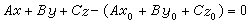。设
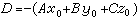，平面 π的方程即Ax+By+Cz+D=0（A、B、C不全为0）。这种形式的方程，叫平面方程的一般式。如果M1(x1，y1，z1)，M2(x2，y2，z2)，M3(x3，y3，z3)是不共线的三点，它们的向径分别为r1、r2、r3设M(x，y，z)是通过M1、M2、M3三点的平面π内的任意点，向径为r。那么平面π的向量方程为
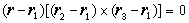。它的普通方程为
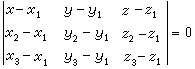或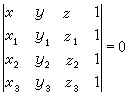
，这种形式的平面方程，叫做平面方程的三点式。如果平面π在Ox、Oy、Oz轴上的截距分别分α、b、с，那么平面π的方程为
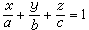。这种形式的平面方程，叫做平面方程的截距式。如果从坐标原点O至平面π的距离为｜OT｜=p（图2
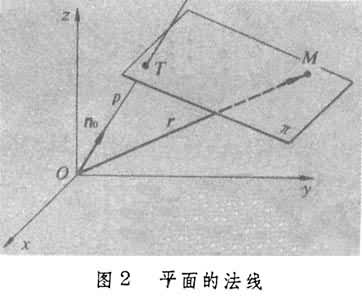）；由O 向π 的方向的单位垂线向量为n0；M(x，y，z)是π内任意点，其向径为r，那么π的向量方程为r·n0-p=0。它的普通方程为
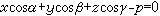(α、β、γ分别为向量n0与Ox、Oy、Oz三轴的夹角)。这种形式的平面方程，叫做平面方程的法线式。在同一直角坐标系Oxyz中，一平面的方程一般式为Ax+By+Cz+D＝0，方程的法线式为
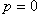，那么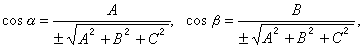
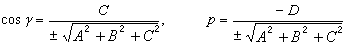
一平面
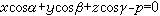至一定点M0(x0，y0，z0)的距离为
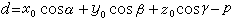。如果此平面的方程为Ax+By+Cz+D＝0，那么
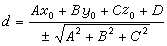（根式符号与D的符号相反）。若平面 π1、π2的方程分别为
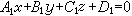和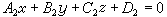
，π1、π2夹角的余弦为：
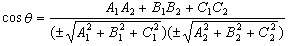（符号选取与前述同）。π1与π2平行的充要条件为
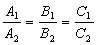。当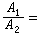
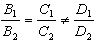时，π1和π2不交；当
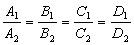时，π1和π2重合。π1与π2垂直的充要条件是A1A2+B1B2+C1c2=0。在空间直角坐标系Oxyz中，
建立了坐标向量后，过定点M0(x0，y0，z0)且与一非零向量n{l，m，n}同向的直线的向量方程为r＝r0+tn，其中r0为M0的向径，r为直线上任意点M(x，y，z)的向径，t为任意实数，化为普通方程为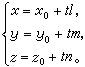
在空间直角坐标系中，这种形式的直线方程，叫做直线方程的参数式。方向系数为l、m、n，且过定点M0(x0，y0，z0)的直线方程为
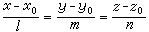，这种形式的直线方程，叫做直线方程的标准式。通过两定点M1(x1，y1，z1)和M2(x2，y2，z2)的直线方程为
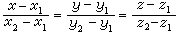，这种形式的直线方程，叫做直线方程的两点式。通过一直线的两个平面方程联立，也作为这直线的方程。一般地，两平面方程联立：方程组
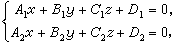其中相当项系数不成比例时，即为一直线的方程。这种形式叫做直线方程的一般式。两直线 
共面的充要条件为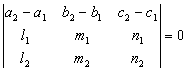
。方程仍如上述的两直线夹角的余弦为
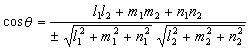，式中符号依两不同角选取。方程仍如上述的两直线，其垂直的充要条件为
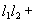
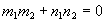。其平行的充要条件为
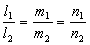。如果一直线的方程为
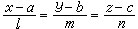，一平面的方程为Ax+By+Cz+D=0，那么它们的夹角的正弦为
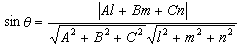。方程仍如上述的直线和平面平行的充要条件为Al＋Bm＋Cn＝0；垂直的充要条件为
。
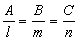