序数(卷名：数学)
ordinal number
集合论基本概念之一，是日常使用的第一、第二等表示次序的数的推广。序数概念是建立在良序集概念之上的，而良序集又是偏序集、全序集的特殊情形。
偏序、全序和良序 次序是二元关系（见映射）的一个非常重要的类型。设R是定义在A上的满足下列条件的二元关系：①对于一切x∈A有xRx（自反性）；② 对于一切x，y∈A，由xRy与yRx可得x=y（反对称性）；③对于一切x，y，z∈A，由xRy与yRz可得xRz（传递性），就称R是定义在A上的偏序，也称半序。偏序R通常记为≤或
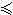，α≤b)读作α在b前。集合A连同其上定义的偏序≤，称为偏序集，记为〈A，≤〉。实数集上的通常的大小关系、集合之间的被包含关系、自然数之间的可整除关系都是偏序的例。设≤为A上的偏序。如果在A上定义一个关系<，使得x<y当且仅当x≤y且x≠y，则关系<满足条件：①′对任何x∈A，x<x不成立，②′由x<y与y<z可得x<z。这时<称为严格偏序。反之，设<为严格偏序，如果定义x≤y当且仅当x<y或x=y，则≤必为偏序。因此在偏序与严格偏序之中只需讨论一种就够了。设〈A，≤〉为一偏序集，如果x0∈A且在A中没有其他x使x≤x0，则称x0为A的一个极小元（素）。如果对于一切x∈A有x0≤x，则称x0为A中的最小元（素），正整数集在整除的偏序下1是最小元，但若只限于大于1的整数，则只有极小元（每个质数）而无最小元。仿此可定义极大元与最大元。设x为偏序集〈A，≤〉的子集，如果存在α∈A，使得对于一切x∈x，有α≤x，则称α为x（关于A）的一个下界。如果x的关于A的一切下界有一最大元α0，就称α0为x（关于A）的下确界，记为infx。仿此可定义上界和上确界，后者记为supx。A上的偏序≤，如果再加上条件④对于一切x，y∈A，总有x≤y或y≤x（至少有一成立），就称≤为A上的全序，也称线序。〈A，≤〉称为全序集。显然，在全序集中x<y，x=y，x>y，三者必居其一且仅居其一。实数集及其任何子集在通常的≤关系下是全序集的例。对于全序集〈A，≤〉如果再加上条件⑤A的任一非空子集都有最小元，就称≤为A上的良序，〈A，≤〉称为良序集。按任何顺序排起来的有限集，按自然顺序的自然数集，将所有奇数排在前面、所有偶数排在后面的自然数集{1，3，5，…，2，4，6，…}都是良序集之例。但整数全体，区间［0，1］，就不是良序集。设<A，≤1>，<B，≤2>为两个偏序集，如果存在A到B的双射φ使得对于一切x，y∈A，x≤1y当且仅当φ(x)≤2φ(y)，便称两偏序集为序同构，记为A埍B。例如奇数集与偶数集序同构，但是上面列举的三个良序集没有两个是序同构的。序数的定义 序数原来被定义为良序集的序型，而良序集A的序型凴，作为从A的元素的属性中抽象出来的结果，是所有与A序同构的一切良序集的共同特征，即凴定义为{B｜B埍A}。这个定义从形式上看来是十分简单明瞭的，但在ZFC公理系统中不能证明它构成一个集合。事实上，{B｜B埍A}是一个真类。因此，原来的那个定义是不成功的，必须修正，另走别的途径。设 α是一个良序集，ξ∈α，称S(ξ)＝{β∈α|β<ξ}为在良序集α中由ξ所生成的初始截段。1923、1928年，J.冯·诺伊曼把序数定义为满足下述条件的良序集α:对于一切ξ∈α，S(ξ)=ξ。例如在集合9={0，1，2，…，8}中取一个元素2，S(2)={0，1}=2，9中任何其他元素也具有这个性质，所以9是一个序数。
集A称为归纳集，如果①═∈A，②只要α∈A就有α′＝α∪{α}∈A。归纳集A的存在性是由无限公理保证的。A的一切归纳子集之交N称为自然数集，它是最小的归纳集。N是良序的，并且其中任一元素n的初始截段S(n)={0，1，2，…，(n-1)}=n，所以N是一个序数，这个序数通常用ω表示。N 的每一个元素n都是序数，称为有限序数。有限序数以属于每一个归纳集作为特征。其他序数称为超限序数，ω 就是最小的超限序数。1937年R，M.鲁宾逊给出了序数的另一等价定义，良序集<α∈>是一个序数，若〈α，∈〉是传递集，即只要x∈α且y∈x就有y∈α，这些定义没有康托尔原来定义的缺点。
序数有三种，第一种是0；第二种是某一序数α的后继α′=α∪{α}，称为后继序数；其他序数属于第三种，称为极限序数。对于任何良序集A，必有一个且仅有一个序数α使A与α序同构，此时α称为A的序数，用凴 =α表示。任何两个具有相同序数的良序集，必定序同构，因此序数是同构良序集的共同特征，这正是康托尔序数概念的实质。
序数的算术 设αξ（ξ<λ）为一序数列，在集合A=
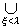
中规定其任意两个元素〈γ，i〉、〈δ，j〉的次序如下：<γ，i>＜<δ，j>当且仅当i＜j或者i=j且γ＜δ；则〈A，＜〉构成一个良序集。A的序数可定义为序数列αξ(ξ<λ)之和，用
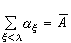表示之。特别地，当λ=2，α0=α，α1=β时，
可简写为α+β；当对于任何ξ<λ，αξ=α时，可写成α·λ，称为两个序数α，λ的乘积。对于任何序数α、β、γ，它们的加、乘运算满足:①结合律，(α+β)+γ=α+(β+γ)，(α·β)·γ=α·(β·γ);②左分配律，α·(β+γ)=α·β+α·γ。但交换律与右分配律对序数的和、积却并不成立，例如:ω+1>ω=1+ω;ω·2>ω=2·ω；1·ω+1·ω=ω·2>ω=(1+1)ω。由于全体序数构成一个真类（布拉利-福尔蒂定理），因此对于任何极限序数λ，序数列{αξ|ξ<λ}总有上界，且必然存在最小的上界，它就是序数列{αξ|ξ<λ}的上确界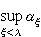
。设α，β为序数，归纳地定义αβ如下：
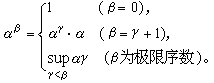对于任何序数α、β、γ，序数的幂满足：①同底幂的积，
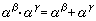；②幂的幂，
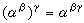。序数的幂运算不满足“积的幂”性质：
。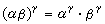