声波(卷名：物理学)
sound wave
媒质中传播的质点位置、压强和密度对相应静止值的扰动。媒质包括气体、液体和固体。过去把固体中这种扰动叫做应力波或弹性波，现在仍有沿用这种叫法的，特别是在力学中。近年来声学逐渐把固体中的应力波列作声波，也从声学角度加以研究，这是因为声波的应用对象，越来越多地包括固体，诸如金属、压电体、铁磁体、半导体、岩体、复合材料、人体。本条将只限于讨论流体（气体或液体）中的声波，关于固体中的声波见固体中的弹性波。
扰动是指声波到达后，有关量的瞬时值对声波未到达前原有值的差异。流体的质点位置、压强和密度都是紧密联系的，其中一个量有扰动，其他量也会相应有扰动。而且还有更多的派生扰动，如质点速度。流体中扰动在传播，但流体本身并不显著流动。扰动起源于流体某处有个振动的物体，物体的振动驱使流体产生和传出扰动。声波扰动是机械的，声波在传播中带有机械能量。
流体中的声波常称为压缩波或压强波，是纵波，严格地讲，在粘滞流体中也产生一种横波，但在一般流体中，则这种横波在空间剧烈衰减，以致很难探测到（见波）。
声波中的扰动，很多时候非常微小，以致在运动方程中，扰动的二次方项或两个相异扰动的乘积，比起扰动的一次项来，可以忽略。这类声波叫做线性声波或小振幅声波；否则就叫非线性声波或有限振幅声波。忽略二次项和更高次项与否，不只是数学处理的简与繁的问题；线性波与非线性波有相当大的性质差异。从发展史看，线性波很早就得到大量的研究，它的重要性在于，人类日常生活中几乎无时或息的声音，几乎都是线性波。人们大声讲话时，空气中质点的位移振幅只有几十纳米的数量级，而压强的微扰对大气压强之比以及密度的微扰对原有空气密度之比只有百万分之一的数量级。
按人耳对频率的感应，声波随频段分为次声波(20Hz以下)， 可听声波(20～20000Hz) 和超声波（20000Hz以上）。超声波有时还再细分。
线性声波 对最基本形式的线性声波，只考虑载波流体的惯性和压缩性。当振动着的声源或毗邻流体质点作用于一个流体的质点时，惯性驱使后者前进，压缩性却提供了恢复力，压使它适时回缩。这类似于一个受弹簧牵制的物体。在数学上采取线性化处理后，流体的质点位移、逾量压或逾量密度都是空间坐标和时间的函数，满足标准的波动方程。逾量压也叫声压，指瞬时压强减去静止或平衡压强。逾量密度指瞬时密度减去静止或平衡密度。
声速 考虑到流体受压缩会局部升温，理想气体中的声速是
式中γ是比热容比，R是摩尔气体常数，T是热力学温度，M是摩尔质量。在1个大气压、20摄氏度时空气中
的计算值是340米每秒，同实测声速值是相符的。这是线性理论有意义的一个重要依据。对理想流体，声速是
，式中p和ρ分别是流体中的瞬时压强和瞬时密度，下标ad表示绝热。声衰减 非平面波的振幅会在传播中衰减，例如球面波的球面随传播而增大，因此声波的能量分散了，声波传得越远会越弱。除了这种几何发散外，实际流体的粘滞性和导热性以及分子内部结构对声波的弛豫等性质，还会导致对声波（包括平面波）的吸收(见声吸收)。因此，声波也在传播中衰减。
弛豫现象不仅引起声吸收，而且会导致声波相速随频率的改变（即频散）。此外，在有限尺寸的（即使是理想的）流体中，声波也可以有频散，称为位形性频散。
声波的能量 包括动能和势能，前者起源于流体的惯性，后者起源于压缩性。能量是扰动的二次方项。在描述声波的线性理论中，曾经忽略运动方程中的微扰二次项，但在考虑声能时，却要保留二次项，而只忽略三次或更高次项。可以证明，在非频散流体中，单位体积的平均声能，或叫声能密度，是
式中μ是质点速度矢量， p和po是压强的瞬时值和平衡值，即p-po是声压，ρo是密度的平衡值，下标av指时间平均。描述声能传输的快慢和方向的量，称为声强，它是个矢量，以I)来表示。声强是单位时间内声波通过同其传播方向相垂直的单位面积平均输运的能量
沿着以单位矢量n 表示的指定方向，单位时间内通过单位横截面的平均输运能量是I)·n。
平面简谐波的时间平均声能密度是
声强是
这里 pm和μm分别是声压和质点速度的幅值。声波的传播 声波在进行中遇到障碍物，会受到干扰。先考虑简单的情况，一个流体中传播的平面声波遇到另一个流体，而两个流体间的界面是和声束相垂直的平面，平面的面积远大于声束的截面。这时声波将部分反射，部分透射。设入射声压是
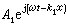，反射声压是
，透射声压是
，其中k1、k2分别是第一流体和第二流体中的圆波数，с1、с2分别是它们中的声速，
。这里采取了通常的做法，用复数函数来代替正弦函数或余弦函数。可以证明：
其中ρ1、ρ2 分别是两个流体的静止密度。如果ρ2с2＝ρ1с1，那么B1=0，A2=A1，声波的前进不受影响。从这些关系可以看出，不同的媒质，表现在它们的ρс这个乘积不一样，不仅在声波的反射问题上，在其他许多声波性质的问题上，也可得出同样的结论。因此ρс是声学中很基本的一个量。实际上，它是沿正x方向传播的平面波在流体中声压p和质点速度μ之比
叫做声阻抗率，也叫特性阻抗。它的单位是帕秒每米。对平面波，p/μ是个实数，即是声阻率。假如平面声波是沿负x方向传播，则
对球面波，p/μ是复数。平面声波在两个流体之间的平面界面上如果是斜入射，也存在反射、折射现象，入射角θi和折射角θt之间满足关系：sinθi/sinθt=с1/с2。
声波在前进中，常会遇到尺寸有限、形状不等、ρс迥异的障碍物。这时不是单纯反射，还出现衍射。总的现象常称为散射。散射是声学中一个很基本的问题，也是声波应用中一个很重要的问题。海洋里声波遇到潜艇，人体中声波遇到肿瘤，将怎样反应，这些都是在不断探索的问题。
声波不仅在遇到障碍物时常有复杂的反应，即使在一个流体，这个流体可能是不均匀的：或者有温度分布，或者有成分变化，或者有一部分在运动等等。对线性声波的传播，还有许多人们没有认识的问题。至于怎样产生和测量人们所需要的声波，待了解的问题也不少。
非线性声波 前面提到，考虑流体中传播着的微小机械扰动，是有积极意义的，因为日常的声音便属于这类声波。但是自然界中也有不少并不那么微小的机械扰动，例如爆炸所发声波。实验室内目前也在有意识地来成功地产生高强声，例如为了试验火箭的发射对多种部件的疲劳作用。这些声波便是有限振幅声波或非线性波。在数学处理上，这时不能只保留扰动的一次项或线性项。或者仍然采用微扰方法，而保留二次或更高次项，或者在极少数可能时不作任何近似，求算波动的精确解。
以一个在起点是平面正弦波的传播作例，来看一看大振幅的后果。仍假定传播媒质是最简单的，是一个无粘滞性、无导热性、均匀的无限大流体。在这简单情况下，线性正弦波会无变动地向前传播，保持正弦形状，以固定的速度运行。非线性正弦波却不这样。100 多年前已得出的精确解表明，波的传播速度不是整体一致的。波轮廓的不同点具有不同的传播速度；稠密部分的声速大于线性波的声速，而稀疏部分的声速要小些。结果是，在传播过程中，正弦波的轮廓不断变化，逐渐陡峭，向锯齿形状转化。从频谱角度来看，实质是，在传播过程中，逐渐产生原来频率的高次谐波，基频能量不断地转给谐频。等到传播足够远时，正弦波完全变成锯齿形。可是这时竖直部分要出现扰动量的不连续，这个结论在物理上看来是不现实的。
实验上却确实观察到高强度正弦声波向锯齿波的转化，所以上述理论结果并不是全无根据的。可能只需要对所取物理模型作些修正。假若考虑更实际些的媒质，首先是像对线性声波的讨论中那样，考虑有粘滞性和导热性的流体，果然发现，扰动的完全不连续性并不出现。这时的二级近似理论表明，波形仍将畸变，正弦波仍将转变到接近锯齿波，但不会形成完全的不连续，而只会形成很薄的过渡层，可能薄到分子自由程的数量级，却仍是有限厚度。波再向前进，粘滞性和导热性的耗散作用更发挥出来，使过渡层变厚，波形逐渐恢复到几乎再成正弦形，振幅当然也减小。
另举一个阐明非线性声波传输特性的例子。前面提到，线性的一个基本特征是，线性波可以叠加。两个线性波相遇，在重叠区只要把各点各自的振幅矢量相加，便可得出总的波。非线性波却不满足叠加原理，这意味着一个有限振幅声波和另一个有限振幅声波要相互作用。假设有圆频率分别为
1和2(≈1)的两个非线性平面波，同时沿同方向前进。在并进的过程中，这两个波会互相干涉，产生频率分别为m1、n2以及m1±n2的许多波，这里 m、n是正整数。这里面圆频率为1-2的差频波，在离开声源一定距离之外，可以强度超过原来的两个平面波。在起始的两个平面波原来就比较强的情况下，这个差频波还可以发展成激波。非线性声波又可以作用于媒质自身，产生一些非波动现象，例如产生媒质中的声流，即媒质的非周期流动。
对非线性声波的研究，虽然19世纪就已开始，但直到近些年才较快发展，这是由于生产上的新需要。目前不少问题有待探讨。
见非线性声学。