复变函数逼近(卷名：数学)
approximation to complex functions
在复平面的某个闭集 F上用较为简单的函数（例如多项式或有理函数）来近似地表示较为复杂的函数（例如ƒ(z∈A(F)，A(F)表示所有在F上连续，在F的内部F0上解析的函数类）。复变函数逼近的历史最早可以追溯到1885年的龙格定理：设 F的余集F0是含有∞的区域且ƒ(z)在F上解析，则有ƒ∈P(F)，P(F)表示所有在F上能被多项式逼近的函数ƒ构成的类，即任给ε>0，存在多项式P， 使
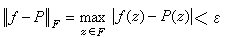。这里要求ƒ在F上解析的条件是很强的，因此以后有不少工作就从事于减弱这个要求。此外还研究用有理函数、亚纯函数、全纯函数的逼近以及研究这些逼近的速度，这就是通常函数逼近论中的各种定性及定量问题，各种空间中的逼近等等。由于复平面上集合F 的复杂性以及函数类的多样性，给研究带来了种种困难。早期J.L.沃尔什、М.Α.拉夫连季耶夫、M.B.克尔德什、M.M.杰尔巴强、A.Л.沙吉尼扬、C.H.梅尔捷良以及近期的A.Γ.维图什金、A.A.贡恰尔、B.K.贾德克及他们的学生们都作出重要的贡献。目前复变函数逼近论已发展成为函数论中的一个重要分支。紧集K上的多项式逼近 最主要的结果是在 1951年由梅尔捷良得到的，从此结束了1885年由龙格开始，经过沃尔什(K是约当曲线或约当弧)，拉夫连季耶夫（K0=空集Ø），克尔德什(K是闭区域)等一段漫长的历史。梅尔捷良的结果如下:要使A(K)=P(K)的充要条件是K0是区域。事实上，梅尔捷良得到更为一般的有理函数逼近的结果，并且还得到了逼近速度的估计式。
紧集K上的有理函数逼近 当紧集K的余集Kc不是区域时，自然会提出有理函数的逼近问题。当Kc是由有限多个连通分支组成时，正如梅尔捷良指出的那样，有理函数逼近总是成立的。但当Kc是由无限多个连通分支组成时，情况就复杂多了。1938年A.罗思指出，存在函数ƒ0∈A(K)，但ƒ0唘R(K)(R(K)表示所有在K上能被有理函数逼近的函数ƒ构成的类，即任给ε>0，存在有理函数R，使
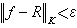)。因此有兴趣的是寻找加在K上的充要条件，使得A(K)=R(K)。1959年维图什金对于无内点的K，彻底解决了这个问题。但是对于一般的K，只是在1967年才给出了完美的解决。为了叙述这个重要的结果，先定义1962年Ε.∏.多尔任科引进解析容量的概念:设E是有界集，C(E，1)是所有在全平面上连续，其模不大于1，在∞处取值为0，且在E的一个紧子集的余集上解析的函数所构成的集合，则定义E的解析容量为 
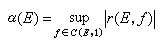，其中r(E，ƒ)为ƒ∈C(E，1)在∞处的留数。维图什金的结果为：A(K)=R(K)的充要条件为下列两者之一：① 对任意有界开集G，有α(G\\Kc)=α(G\\K)；
② 对K的边界дK上任意点z，有
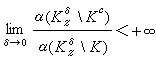，式中K寋是以z为中心半径为δ的圆。此外还研究按K的面积平均逼近，以及区域边界上的积分平均逼近等问题。
闭集F上的亚纯函数逼近 设G是区域，用M (G)记在G内亚纯的函数类。设F嶅G，在F上用M (G)中的函数逼近A(F)中的函数问题比用有理函数进行逼近更为广泛，但又与它密切相关。1976年罗思证明，ƒ∈A(F)在F上能被M (G)中函数逼近的充要条件是对于任何一个紧子集K嶅F，有
(
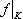为ƒ 在其定义域的子集K上的限制)。由此可以得到很多特殊情况下的结果，例如ƒ在F上全纯（即解析）时，ƒ 就可以在F上被M (G)中函数逼近。闭集F上的全纯函数逼近 设G是区域，用Hol(G)记在G内全纯(解析)的函数类。设F嶅G，用G*记G加一个理想点“∞”以后的单点紧化区域：
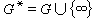。1968年H.Y.阿拉克良得到，ƒ∈A(F)可以通过Hol(G)中函数在F上逼近的充要条件为:①G*\\F是连通集;②G*\\F在∞处局部连通，即对∞的每一个邻域U，存在一个连通集Z嶅U，使得 ∞为Z的内点。这个结果在研究解析函数的边界性质和函数值分布理论中有很重要的作用。相切逼近 粗糙地说，就是可以以任意快的速度实现逼近。设G是区域，闭集F嶅G，ƒ∈A(F)。若对F上任意正连续函数ε(z)，存在g∈Hol(G)，使得|ƒ(z)-g(z)|<ε(z)(z∈F)，则称ƒ在F上有相切逼近，此时称F是G内的卡莱曼集。关于亚纯函数逼近也有类似的定义。最早卡莱曼对G是整个复平面，证得整个实轴是卡莱曼集。后来克尔德什与拉夫连季耶夫对于G是整个复平面，给出了一般的没有内点的闭集F是卡莱曼集的充要条件:存在一个正值函数r(t)↑+∞(t→+∞)，使得对于F的余集Fc上的任何一点ζ，可以用一条位于F∪{｜z-ζ｜<r｜ζ｜}外的曲线将ζ与无穷远点连结起来。Α.Б.涅尔谢相对于一般的G与F给出了F是卡莱曼集充要条件。
非卡拉西奥多里区域G的逼近 若区域G的边界不等于闭区域強的余集強c的边界，则称G为非卡拉西奥多里区域。这类区域最典型的有带有割线的约当区域或等价于相切于一点的两个圆周所围成的“月形区域”。对于这种区域ƒ(強)≠P(強)，因此可以提出加权逼近问题：对ƒ∈A(強)，
是否成立，其中h(z)是定义在強上的某个正函数，称e-h(z)为权函数，而下确界是对于所有多项式取的；或按面积平均逼近的问题：
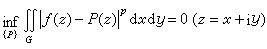是否成立。1939年克尔德什指出，对于強c不连通的G，多项式系按面积平均逼近是否成立的问题不仅依赖于区域G 的拓扑性质，而且在本质上还依赖于区域G的度量性质。例如，对于月形区域，如果在其交点处收缩得很快，则逼近就成立，否则就不成立。沙吉尼扬就给出了逼近成立的必要和充分型的判别法，他的必要性判别法是精确的。后来杰尔巴强给出了精确的充分性判别法。目前还有很多工作研究多项式在无界曲线和无界区域上的逼近问题，更一般地，研究函数系
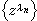的线性组合和其他函数系在无界曲线和无界区域上的逼近问题，其中{λn}可以是复数序列。定性理论 Α.Η.柯尔莫哥洛夫得到了复数域上最佳逼近多项式的特征性质:设φk(z)(k=0，1，2，…，n)，ƒ(z)都是紧集 K上的连续函数，要使
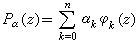是{φk(z)}的线性组合在K上为ƒ 的最佳逼近元的充要条件是对于任何的多项式
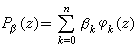，有
，其中最小值是对于使｜ƒ(z)-Pα(z)｜在K上达到最大值的全体点取的。由此可以得到通常函数逼近论中的切比雪夫定理。由于直接应用这个结果来找最佳逼近元不是很方便，因此Ε.Я.列梅兹、Β.К.伊万诺夫等找出了一些比较适合于具体应用的分析方法。定量理论 象通常函数逼近论中一样由正定理和逆定理两部分组成，反映了函数的结构性质与最佳逼近值趋向于零的速度之间的关系。设K是紧集，l=дK是其边界。又设Kc是单连通区域，函数z=ψ(w)将｜w｜>1共形映射到Kc，ψ(∞)=∞，ψ′(∞)>0，而w＝φ(z)是其反函数。设ψ(w)在│w│≥1上连续，在│w│=1上绝对连续，且ГR是在映射z=ψ(w)下│w│=R>1的像，称它为等势线。记
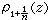是z∈l到
之间的距离。最早，С.Η.伯恩斯坦、W.E.休厄尔在补充假设了ƒ(z)在ГR(R>1)内解析的条件下，得到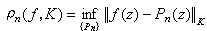
趋向于零的速度至少为1/Rn，其中Pn是n次多项式。后来，梅尔捷良，С.Я.阿尔佩尔在关于边界 l的光滑性作出种种假设下，对ƒ∈A(K) 研究了ρn(ƒ；K)→0的速度。1972年 T.科瓦里对逐段光滑边界研究了 ρn(ƒ；K)。 近年有不少工作研究｜ƒ(z- ρn(z)｜的点态估计，代替了通常函数逼近论中的阶1/n，这里用 
来刻画。贾德克及其学生们在这个方向上得到一系列结果。他们的区域是很广泛的(只要区域K的边界上任意二点之间的弧长与弦长之比有界就行)。这里叙述Β.И.别雷的结果:设l是│w│=1经过q拟共形变换而得到的闭曲线。若ƒ∈A(K)且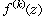
在K上连续，则对任何自然数n≥k，存在n次多项式Pn(z)，使
式中с为常数，w(ƒ，δ)为连续模。关于逆定理，关键是要得到一个伯恩斯坦型的不等式。复变函数插值 这里典型的问题是：给了两个复数序列{zi}，{wi}，其中zi互不相同，研究在什么条件下存在ƒ(z)（有一定的分析性质），使 ƒ(zi)=wi(i=1，2，…)。这里{zi}经常位于复平面上的某个区域G 中（G也可以是全平面）。对于函数ƒ(z)除了解析性以外，还可以要求满足一些其他的条件。例如，设G是|z|<1，|zi|<1，可以要求ƒ(z∈hp，0<p ≤∞(见hp空间)。R.奈望林纳在h∞中考虑这个问题，给出了加在{wi}上的一个充要条件，但是这个条件很不实用。1958年L.卡尔森解决了这个问题，用求极值的方法给出了一个容易判别的充要条件：
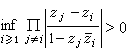。但是他只给出了存在性的证明，且方法也较复杂。1961年M.S.夏皮罗和A.L.希尔兹利用对偶原理对hp(1≤p ≤+∞)空间解决了这个问题，其充要条件仍是上述条件。他的方法比较简单，但是只是对h2才给出结构性的证明。1974年杰尔巴强提出重插值问题，他设{zi}中可以有相同的，且用 sk表示 zk在 {z1， z2，…， zk}中出现的次数，则可以问，要使在hp(0＜p ≤+∞)中存在函数ƒ(z)，满足
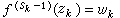的充要条件是什么?杰尔巴强及其阿尔美尼亚的同事们用双正交函数系的方法在假设
的条件下（这也是必要条件）得到的充要条件是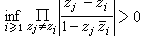
（预先假设sup{sk}<+∞）。他们还在上半平面hp空间研究这一类问题，这与不完备函数系的完备化，不完备函数系闭包中基函数等一系列问题有关。
复变函数插值中另一类问题是:在区域強上给定点列{zi}，设函数ƒ(z)在G内解析，強上连续，n次多项式Pn(z)满足Pn(zi)=ƒ(zi)，1≤i≤n+1，问Pn(z)在強上是否一致收敛到ƒ(z)。一般说来，这是不成立的。对函数ƒ(z)和{zi}进一步加什么条件才可能成立，这方面也有一些研究工作。
此外还可以在全平面上研究这一类问题，且要使函数ƒ(z)为有穷级整函数或其他类型函数。这方面A.Ф.列昂季耶夫做了很多工作，并在研究狄里克雷级数及其他一些问题中有大量应用。
如果将ƒ(zi)看作泛函，则A.O.盖尔丰德研究了一般泛函的存在问题，其中也包括所谓阿贝尔-贡恰洛夫问题，即求函数ƒ(z)，满足
。盖尔丰德还应用牛顿级数解决了希尔伯特一个有关超越数的问题。