复叠空间(卷名：数学)
covering space
代数拓扑中的一个重要概念，又称覆盖空间。设p:塣→X是连续映射，如果在X中，每一点x都有开邻域U，使得p-1(U)是塣中一组互不相交开集｛Uα｝的并集，且p 限制在每个Uα上都是从Uα到U 的同胚，则称p 是复叠映射，塣是X 的一个复叠空间。
例如，由
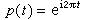规定的直线到圆周的映射 p:E1→s1是复叠映射。设
，取正数
，作z0的开邻域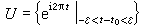
，则p_1(U)是一组不相交开区间｛(n+t0-ε，n+t0+ε)｝的并集，且p:(n+t0-ε，n+t0+ε)→U是同胚。又如，当将n维球面Sn的每对对径点粘合时，商空间是实射影空间Pn，粘合映射p:Sn→Pn也是复叠映射。复叠映射的提升性质 复叠映射是一个纤维映射，即它对任何空间都有同伦提升性质（见同伦论）。此外，它还有更多的提升性质：
映射提升定理 设Y连通、局部道路连通，y0∈Y，又设ƒ:Y→X 是连续映射，x0＝ƒ(y0)，取定慜0∈p_1(x0)，则ƒ 有提升 愝: Y→塣 使 愝(y0)= 慜0 的充分必要条件是ƒ
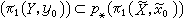。映射提升惟一性定理 设Y连通，ƒ:Y→X是连续映射，ƒ的两个提升愝，愝′:Y→塣如果对某点y∈Y有愝(y)= 愝′(y)，那么愝=愝′。
用这两个定理不难推出，当n>1时，复叠映射 p所诱导的同态p
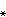:πn(塣)→πn(X)是同构，而p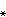:π1(塣)→π1(X)是单同态。泛复叠空间 当P
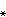(π1(塣))是π1(X)的正规子群时，称塣是X的正则复叠空间；如果塣是单连通的，则称塣是X的泛复叠空间，它是最常用的复叠空间。当一个拓扑空间X连通，局部道路连通与半局部单连通时，它一定存在泛复叠空间。
复叠变换群 是复叠空间塣 的自同胚群的一个子群，它由全体满足p。φ =p的自同胚φ（称为复叠变换）组成。
如果塣是泛复叠空间，并且X道路连通，则塣上的复叠变换群同构于π1(X)，利用这个事实可计算某些空间的基本群。例如E1是S1的泛复叠空间，E1上的复叠变换就是移动距离是整数的平移，从而复叠变换群≌Z，这样就得到
。又如n≥2时，Sn是Pn的泛复叠空间，复叠变换只有两个:恒同映射与对径映射，于是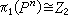
。除了可用来计算基本群外，复叠空间在不动点理论的研究中是一种有效工具，并且在代数拓扑各个领域和几何拓扑中还有广泛的应用。
参考书目
M.A.阿姆斯特朗著，孙以丰译：《基础拓扑学》，北京大学出版社，北京，1983。(M.A.Armstrong，basic TopoЛogy，McGraw-Hill，London，1979.)