复流形(卷名：数学)
complex manifold
具有复结构的微分流形。即它能被一族坐标邻域(见微分流形)所覆盖，其中每个坐标邻域能与n维复空间Cn中的一个开集同胚，从而使坐标区域中的点具有复坐标 (z1，…，zn)，而对两个坐标邻域的重叠部分中的点，其对应的两套复坐标之间的坐标变换是复解析的。称n 为此复流形的复维数。一个n 维复流形也是2n维的(实)微分流形。
作为一维的复流形的黎曼面的研究有着悠久的历史，而一般复流形的研究从20世纪40年代才开始。现在，它已成为近代数学中十分重要的概念和课题。
最简单的复流形是复数平面C及复欧氏空间Cn。
考虑R3中的单位球面。它可以被球面分别去掉北极和南极所得到的两个坐标邻域所覆盖。用关于北极的球极投影得到一个坐标映射，而关于南极的球极投影后再取共轭复数又得到另一个坐标映射。这样，单位球面也构成一维复流形，称为黎曼球面。
对复射影空间CPn描述如下：设Cn
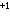是复n+1维的欧氏空间，Cn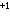\\｛0｝是 Cn+1中非零点全体。对其中两点 
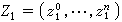和
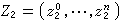，如存在α ∈C 使
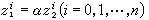，则称 Z1和Z2等价，(z嬼，…，z嬪)称为此等价类的齐次坐标，CPn就是上述这种等价类的全体，它是n维复流形。事实上CP1和黎曼球面是同构的。对CPn中的任一点p，Z=(z0，…，zn)是它的齐次坐标，那么
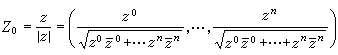是Cn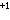
中以原点为球心的单位球面S2n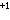中的一点。由p点所确定的S2n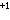上点的全体构成S2n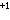中的大圆。因此CPn中的点也可看成S2n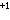中的大圆的全体。如在复流形M 上定义了一个下列复形式
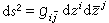的黎曼度量，其中
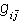是埃尔米特阵，则称此度量为埃尔米特度量，称具有埃尔米特度量的复流形为埃尔米特流形。复流形上总存在埃尔米特度量。在埃尔米特流形中可引进一个二次外微分形式ω，称为凯勒形式，它在复坐标下的局部表达式为
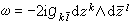。若dω＝0，即ω 是闭形式，称埃尔米特流形为凯勒流形。复欧氏空间Cn关于通常度量
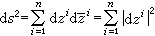是凯勒流形。在复射影空间CPn中有著名的富比尼-施图迪度量，描述如下：设P是CPn中任一点，它确定了S2n
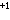中的大圆。CPn在P点的任一切向量X可对应于球面S2n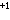中与上述大圆正交的切向量塣，把塣 的长度定义为X的长度。就给出了CPn中的富比尼-施图迪度量;CPn关于这个度量构成凯勒流形。任何黎曼面关于其上任何与复结构相容的黎曼度量也是凯勒流形。如果在复流形M 上有一个黎曼度量，那么由这个度量，对M 上任一点的每个二维平面可定义截面曲率(见黎曼几何学)。如特取某点P处的二维切平面σ为全纯截面，即n维复切空间TpM 的一维复子空间，则相应于σ的截面曲率，称为全纯截面曲率。前面例子中，复欧氏空间关于通常度量的全纯截面曲率为零，复射影空间关于富比尼-施图迪度量的全纯截面曲率为正常数。
参考书目
S.Kobayashi and K.Nomizu，Foundations of Differentia Geometry，Vol.2， John Wiley & Sons， New York，1969.