度量空间(卷名：数学)
metric space
现代数学中一种基本的、重要的、最接近于欧几里得空间的抽象空间。19世纪末叶，德国数学家G.康托尔创立了集合论，为各种抽象空间的建立奠定了基础。20世纪初期，法国数学家M.-R.弗雷歇发现许多分析学的成果从更抽象的观点看来，都涉及函数间的距离关系，从而抽象出度量空间的概念。具体说来，如果X是一集合，d是定义在X×X上的非负实值函数，使得对任何x，y，z∈X有：① d（x，y）=0的充要条件是x=y;② d（x，y）=d(y，x)；③ d(x，z)≤d(x，y)+d(y，z)。这时便称X是一个度量空间，d(x，y)称为x与y之间的距离。
下面是几个度量空间的例子。
欧氏空间Rn 由所有的 n元实数组(x1，x2，…，xn)构成集合Rn，Rn中元素x＝(x1，x2，…，xn)与y＝(y1，y2，…，yn)之间的距离定义为
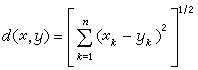。希尔伯特空间H
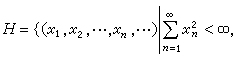
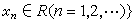其中R表示实数集合。定义元素x=(x1x2，…，xn，…)及y=(y1，y2，…，yn…)之间的距离为
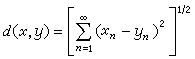。贝尔空间B B={(x1，x2，…，xn，…)│(xn∈R，n=1，2，…)}对于两个不同的元素x=(x1，x2，…，xn，…)及y=(y1，y2，…，yn，…)，用m(x，y)表示满足 xn≠yn的最小标号n，定义x与y之间的距离为
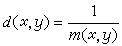；再规定d(x，x)=0（x∈B）。一般假设Ω是任意一个集合，取X={(x1，x2，…xn，…)|xn∈Ω)，可以按同样的方法定义m(x，y)与d(x，y)，得到的度量空间也称作贝尔空间。函数空间 处理分析问题时，根据具体情况需要可以引入种种函数空间。例如，考虑定义于闭区间[0，1]上的一切连续实值函数的集合，就可以定义两个函数ƒ 和g的距离为
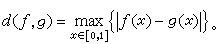
对于度量空间X，可以利用它的度量d 引进一个拓扑结构，其基的元就是所有的开球B(x，r)={y∈x｜d(x，y)<r}。这种拓扑结构称为由度量d 产生；同一集合上，不同的度量可以产生相同的拓扑结构。例如，对于实数集R， d(x，y)=｜x-y｜与
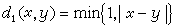就产生同一个拓扑结构。度量不是拓扑概念。完备度量空间 在度量空间中可以用距离定义点列的收敛概念:xn→x0就是指d（xn，x0）。点列{xn}称为柯西点列，是指对任意正实数ε，都存在自然数N，使得m、n≥N时有
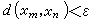。可以证明收敛点列一定是柯西点列，反过来并不成立。每个柯西点列都收敛的度量空间叫做完备度量空间。这类空间有许多好的性质。例如，完备度量空间中压缩映射原理成立。可以用它证明微分方程、积分方程以及无限线性代数方程组的一系列存在惟一性定理。度量空间X的任何子集Y配上原有的距离也成为度量空间，称作X的子空间。如果每个开球{x∈X｜d(x0，x)<r}都含有Y 的点，便说Y是X 的稠密子空间。完备化定理 每一度量空间X 都是另一完备度量空间X
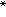的稠密子空间，而且X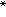由X惟一构造出来。例如，实数直线就是有理数集的完备化，20世纪初建立严密的数学分析理论正是基于这一重要事实。可以证明：在完备度量空间中可数多个稠密开子集的交仍是稠密集。
可度量化拓扑空间 度量空间具有许多良好性质，例如，它满足第一可数公理，它是豪斯多夫空间，正规空间，还是仿紧空间。此外对度量空间而言，紧致性等价于下列三条中的任一条：①任何可数开覆盖都有有限子覆盖;②每一无限子集都在空间中有聚点:③每一点列都有收敛子列。紧度量空间一定满足第二可数公理从而必是可分的。实际上对于度量空间而言，可分性与第二可数公理等价。因此，一个拓扑空间的拓扑结构在什么条件下能作为一个度量空间的拓扑？这是拓扑空间理论的重要问题，称作度量化问题。50年代長田潤一。ю.М.斯米尔诺夫以及R.H.宾得到了可度量化问题的重要结果。例如，拓扑空间可度量化的充要条件是：它是T1正则空间，且具有一个基
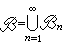，其中每个Bn都是局部有限的开集族。