多值映射(卷名:数学)
multivalued mapping
从集X到集Y的多值映射是一个对应规律F,按照这个规律,对于X的每个元素x,都能相应地得到Y的一个非空子集F(x),称为x对于F的像。对于任何
 嶅X,集
嶅X,集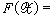
 称为集
称为集 对于F的像;按照F(X)嶅Y或F(X)=Y而说F把X映入或映成Y。特别是,如果每个元素的像集都只含有一个元素,那就是一个单值映射。空间与(单值)映射是拓扑学中两个最原始的基本概念,拓扑学的基本问题──空间的拓扑分类问题,是基于同胚的概念提出来的。而同胚是单值映射,所以单值映射在拓扑学中的地位,显然远比多值映射的地位重要得多。实际上,提出多值映射的概念,出发点不是单纯为了推广,而是着眼于它对其他数学领域的应用。多值映射总是可以化成单值映射来考虑的,即是,如果用2Y表示Y的所有非空子集的集合,那么从X到Y的多值映射F可以视为从X 到2Y的单值映射,记为F :X→2Y。因此,可以像单值映射一样,对于任何
对于F的像;按照F(X)嶅Y或F(X)=Y而说F把X映入或映成Y。特别是,如果每个元素的像集都只含有一个元素,那就是一个单值映射。空间与(单值)映射是拓扑学中两个最原始的基本概念,拓扑学的基本问题──空间的拓扑分类问题,是基于同胚的概念提出来的。而同胚是单值映射,所以单值映射在拓扑学中的地位,显然远比多值映射的地位重要得多。实际上,提出多值映射的概念,出发点不是单纯为了推广,而是着眼于它对其他数学领域的应用。多值映射总是可以化成单值映射来考虑的,即是,如果用2Y表示Y的所有非空子集的集合,那么从X到Y的多值映射F可以视为从X 到2Y的单值映射,记为F :X→2Y。因此,可以像单值映射一样,对于任何 ∈2Y定义它的逆像为
∈2Y定义它的逆像为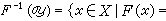
 ,所以对于任何
,所以对于任何 嶅2Y,有
嶅2Y,有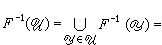
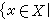
 。设X和Y 都是T1拓扑空间,为了定义F:X→2Y 的连续性,2Y 中的拓扑结构是借助于Y的拓扑结构 τ(Y)给出的,通常有下面三种:对于任何U 嶅Y,定义
。设X和Y 都是T1拓扑空间,为了定义F:X→2Y 的连续性,2Y 中的拓扑结构是借助于Y的拓扑结构 τ(Y)给出的,通常有下面三种:对于任何U 嶅Y,定义 ,
, 于是以
于是以 为子基产生的拓扑结构称为维托利斯拓扑,而以
为子基产生的拓扑结构称为维托利斯拓扑,而以 |
| 或
或 为子基产生的拓扑结构则分别称为上半连续拓扑和下半连续拓扑。在这些拓扑结构下,F:X→2Y(作为单值映射)的连续性分别称为连续、上半连续或下半连续,即是,F:X→2Y称为上半连续的,如果
为子基产生的拓扑结构则分别称为上半连续拓扑和下半连续拓扑。在这些拓扑结构下,F:X→2Y(作为单值映射)的连续性分别称为连续、上半连续或下半连续,即是,F:X→2Y称为上半连续的,如果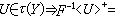
 ;F称为下半连续的,如果
;F称为下半连续的,如果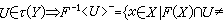
 ;F称为连续的,如果它既是上半连续又是下半连续的;这里F-1<U>+称为集U的上逆像,而F-1<U>-称为集U的下逆像。子集空间2Y的拓扑结构对于由此展开的多值映射理论至关紧要,因此,对于子集空间拓扑结构的研究已经成为点集拓扑学中一个有趣的课题。此外,对于多值映射F:X→2Y还可以提出一个连续选择的问题:在什么条件下存在单值连续映射ƒ:X→Y,使得
;F称为连续的,如果它既是上半连续又是下半连续的;这里F-1<U>+称为集U的上逆像,而F-1<U>-称为集U的下逆像。子集空间2Y的拓扑结构对于由此展开的多值映射理论至关紧要,因此,对于子集空间拓扑结构的研究已经成为点集拓扑学中一个有趣的课题。此外,对于多值映射F:X→2Y还可以提出一个连续选择的问题:在什么条件下存在单值连续映射ƒ:X→Y,使得 ?如果F具有连续选择,那么与F 有关的应用问题几乎都可以归结为单值映射的相应问题。
?如果F具有连续选择,那么与F 有关的应用问题几乎都可以归结为单值映射的相应问题。多值映射的一般理论自然是单值映射相应理论的推广,但前者显然不如后者那么丰富多彩。多值映射理论的重要性在于它对其他数学分支的应用,特别值得一提的,是多值映射的不动点理论对博弈论的完美应用。x∈X称为F:X→2X的不动点,如果x∈F(x)。角谷静夫于1941年首先把关于单值映射的布劳威尔不动点定理推广到多值映射,下面是一个等价形式:
角谷不动点定理 假设K嶅Rn是非空有界闭凸集,F:K→2K是上半连续多值映射,使得对每个p∈K,F(p)都是K的非空闭凸集,于是F有不动点。
命
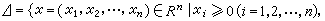
 ,于是K=Δ×Δ嶅R2n是非空有界闭凸集。考虑双线性函数
,于是K=Δ×Δ嶅R2n是非空有界闭凸集。考虑双线性函数 ‖αij‖为实矩阵。对于任何(x,y)∈K,命
‖αij‖为实矩阵。对于任何(x,y)∈K,命 可以证明,F(x,y)嶅K是非空闭凸集,F:K→2K上半连续,所以据角谷定理知,存在(
可以证明,F(x,y)嶅K是非空闭凸集,F:K→2K上半连续,所以据角谷定理知,存在( )∈K,使(
)∈K,使( )∈F(
)∈F( ),即
),即 从而
从而 由于相反的不等式是自然成立的,这就证明了矩阵博弈的基本定理:存在
由于相反的不等式是自然成立的,这就证明了矩阵博弈的基本定理:存在 ∈Δ,使得
∈Δ,使得 现在角谷定理已经得到很大的推广,在博弈论、泛函分析等分支都有广泛而重要的应用。
现在角谷定理已经得到很大的推广,在博弈论、泛函分析等分支都有广泛而重要的应用。参考书目
E.Michael,Topologies on Spaces of Subsets,Tran. Amer.Math. Soc., Vol.71, pp.152~182,1951.
E.Michael, A Survey of Continuous Selections,Lecture Notes in Math.,Vol.171, Springer-Verlag, Berlin, 1970.
C.Berge,Topological Spaces, Oliver and Boyd, Edinbergh and London, 1963.
C. Berge,Théorie Générale des Jeux ╜ n Personnes,Gauthier-Villars, Paris, 1957.