热力学第三定律(卷名：化学)
third law of thermodynamics
表述为在绝对零度时，所有纯物质的完善晶体的熵值为零。1906年德国的物理化学家W.H.能斯脱在实验的基础上提出：当T→0K时，凝聚物系等温过程的熵变ΔS也趋近于0：
这就是能斯脱热定理。它意味着，当温度趋近于绝对零度时，所有凝聚物系的熵值有一个相同的极限值。1912年德国物理学家M.普朗克在能斯脱热定理的基础上，进一步假设当温度趋近于绝对零度时，所有纯液体和纯固体的熵值为零：
然而，后来的实验事实和统计热力学对熵的讨论都表明，有些纯态物质如过冷液体和某些固态化合物在绝对零度时仍有一个正的熵值。为此，美国物理化学家G.N.路易斯和M.兰德尔于1923年在他们合著的《化学物质的热力学和自由能》一书中对普朗克的假设作了修改，指出：在绝对零度时，所有纯物质的完美晶体的熵值为零。这就是现在认为比较严格的热力学第三定律的表述。所谓完美晶体，是表示系统内部已经处于热力学平衡的晶体（即内部完全有序的晶体）。
热力学第三定律和热力学第一定律、热力学第二定律一样，也是人们对某些实验现象加以归纳、总结而提出的一种假设，是无法从理论上加以证明的。
第三定律在热力学中主要用于计算各种指定状态下的熵值。例如，求某气体B在温度为T，压力为p时的摩尔熵值，可设计如下途径：
B(完美晶体，0K)
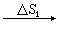B(晶体，Tf)
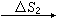B(液体，Tf)
B(液体，Tb)
B(气体，Tb，101.325kPa)
B(气体，T，p)。上述过程中Tf、Tb分别为物质B的正常熔点和正常沸点。熵变ΔS1、ΔS2、…可分别用量热的方法求出(低温下晶体的热容可由德拜公式计算)。将ΔS1、ΔS2、…相加，即为过程B(完美晶体，0K)─→B(气体，T，p)的摩尔熵变ΔSm，根据热力学第三定律，S(完美晶体，0K)＝0，所以上述过程的ΔSm即为物质B在温度为T，压力为p时的摩尔熵值。
由上述方法求出的物质的熵值称为该物质在指定状态下的规定熵或第三定律熵(有些书上称为绝对熵)。若物质处于标准状态，则称该规定熵为标准熵，记作S妔(T)。
1940年英国物理学家R.H.否勒和E.A.古根海姆还提出了热力学第三定律的另一种表述方法：“任何系统都不能通过有限的步骤使自身温度降低到绝对零度。”热力学第三定律的这两种表述方法是互相有联系的，但在化学热力学中第一种说法应用得更广。
参考书目
M.L.McGlashan，Chemical Thermodynamics，Academic Press， London，1979.