涡旋(卷名：物理学)
vortex
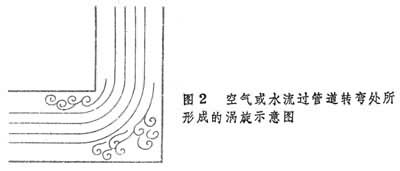
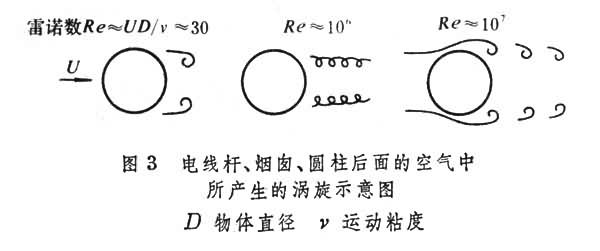
流场中经常见到的不断移动、变形并缓慢向周围流体扩散的有旋度的绳状、环状、椭球形或更复杂得多的运动形状的流体。涡旋的几个图例如图1、图2、图3。涡旋的第一个特点是有旋度
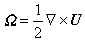，式中U)为流速矢量，Ω也是矢量。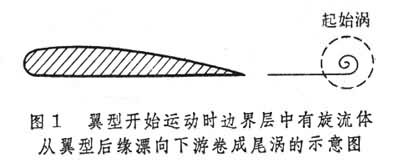
刚体旋转时整个物体的旋度（整体旋转）是同一个量，即刚体旋转时的转速。流体所能承受的切应力比固体的要小的多，因此，在流体质点附近的一个小区域中的流体，会不断变形和旋转（局部的旋转）。除了Ω呏0的位势流和一些特殊例子以外，流场中各点的旋度常常有很大的差别。U)是坐标x、y、z和时间t的函数，U的三个分量为μ、υ、
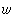。Ω的三个分量为ξ、η、ξ在直角坐标系里也是x、y、z、t的函数，即它们也随位置和时间而变
，
，
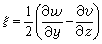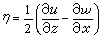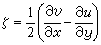。在平面问题中用极坐标r、θ，U的分量为υr、vθ。Ω垂直于平面，它的大小为
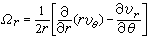。总之，刚体旋转时旋度对整个刚体是同一个量，而流体的流场各点的旋度在空间中一般是不均匀的，且随时间而变。不能把旋度和整个流体的旋转等同起来，例如由μ＝μ(y)、v＝0、
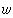＝0所描述的流线都是平行直线的运动；
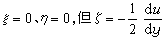这就是有旋运动。也不能把涡旋简单地理解为围绕同一圆心的旋转运动。例如，对r＞0，考虑由
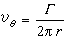（Γ为一常量）、υr＝0所描述的旋转，它是无旋的，即Ω＝0。以图1、图2、图3为例，除了边界层、涡旋以外，流动可以是位势流或称无旋流（Ω呏0，U＝墷嗞，嗞是速度势）。也就是位势流和有旋流各占流场的一部分区域。
粘性的作用使有旋流缓慢地向无旋流区域扩散，同时使有旋区的旋趋于均匀和减弱。如果忽略粘性，也就是忽略缓慢的扩散，那么位势流和有旋流就有明确的界面。这个界面一般说来会移动和变形。有旋区的运动和无旋区的运动会有相互影响。H.von亥姆霍兹在 1858年的论文里和开尔文（即W.汤姆孙）在1869年的论文里都有关于有旋运动的论述。这些著作为20世纪初建立机翼和螺旋桨理论作了极好的理论准备。
流体的涡旋有大有小，有绳状、环状，且在变形过程中会变成外形很不规则的形状。相距不远的若干个涡旋之间还有相互的作用力，并影响各自的运动。除圆柱形涡或椭圆柱形的涡管以外，一般的涡在运动时外边界的形状不断变化，包括分裂。大涡旋会分裂成尺度较小的涡，小的会再分得更小。而很小的涡的动能会由于粘性作用逐渐转变成热能（见流体力学的能量方程）而消失。
湍流（见层流和湍流）是由众多的大小、形状和强度各不相同的涡旋所组成，这是一个尚待深入研究的困难而极为重要的领域。
即使流体涡旋运动很复杂，然而流体力学已阐明了它的若干重要规律，其中之一是下文介绍的环量守恒定理。流体运动过程中由同样的流体质点所组成的线叫流体线。随着流体的流动，流体线的形状和线上各点的欧拉坐标不断随时间变化。环量是在某一时刻，沿流体中任意一条封闭的空间曲线或是沿任意一条封闭的流体线作速度沿此曲线的线积分
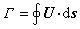，式中Γ就是沿此封闭曲线的环量，U是速度矢量，ds是曲线上的矢元，U·ds是速度矢量在矢元上的投影乘矢元的弧长。斯托克斯定理说明了以封闭曲线为边缘的面上各点旋度的面积分等于沿此封闭曲线的环量。可见，环量可以衡量封闭曲线内全部旋度的总强度。
根据欧拉方程，在1869年发表了重要的环量守恒定理（又称汤姆孙定理或开尔文定理），即在无粘流体的连续流场中，沿任意一条封闭（不和自己相交叉）流体线的环量不随时间改变。这个定理成立的前提是：在连续流场中忽略粘性，作用于流体的体积力有位势（如重力），并且压力p是密度ρ的单值函数p＝p(ρ)，或更简单情况──密度均匀。这个定理有助于判断那一类从静止开始的流动可采用位势流的模型。在流场内任意作一条封闭的流体线，若它是速度均匀的流动，那么沿它的环量是零；又如环量守恒定理的前提都能成立，则这个环量当时间增长时仍保持为零，就是说以后的流动仍是位势流。
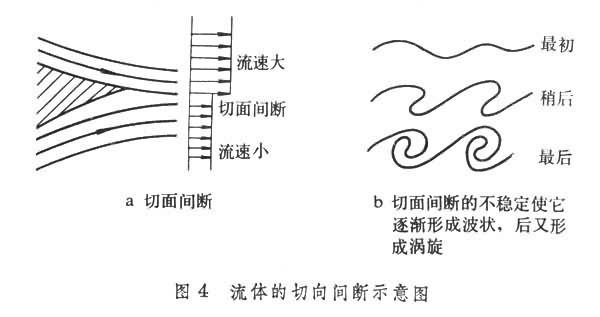
在连续介质力学中，经常把流体质点的速度看作是空间坐标的连续函数。1868年亥姆霍兹曾说明，无粘流体理论中应该允许有一种切向间断面，这个面两侧的流体沿此面某一切线方向的速度可以显著不同。图4a中表示了两股流体的汇合，交界面就是切向间断面。这种间断是不稳定的。在自然界常有偶然的、小的不均匀性，会使切向间断呈现波状曲面。波状弯曲会不断增长，最后变成一个个集中的涡旋，见图4b。这种不稳定性叫亥姆霍兹不稳定性。这是产生涡旋的第一种方式。
产生涡旋的第二种方式是运动流体遇到固体壁或是固体壁在流体中运动，如果流体的大部分相对于固体壁的运动速度足够大时，那么在固体壁附近就会形成很薄的充满旋涡的边界层。边界层中的旋度不是零，也不是位势流。不论边界层中流体从固体壁尽头或是从固体壁某处流动，当它离开固体壁时，都会使有旋度的流体在流场中卷曲成为大大小小的众多涡旋。在前进的车辆、飞行器后面，有风时的建筑物背风面，急流的河床底部和岸边，就是这样造成很多涡旋的。
不同流线上的流体质点通过弓形激波时，在激波的不同部位上熵的增长不同。从欧拉方程可以推论出，如果垂直流线方向的熵有梯度，则旋度同熵的梯度、温度、密度三者的乘积成正比。钝头物体在超声速飞行时，在它前面会产生弓形激波，在弓形激波后边的气流中就会产生涡旋。这是产生涡旋的第三种方式。
涡旋还可因气象条件变化而产生（运动不再是绝热运动，密度有变化），如台风、龙卷风等。