疲劳(卷名：力学)
fatigue
在循环加载下，发生在材料某点处局部的、永久性的损伤递增过程。经足够的应力或应变循环后，损伤累积可使材料产生裂纹 （图1），或使裂纹进一步扩展至完全断裂（图2）。出现可见裂纹或者完全断裂都叫疲劳破坏。法国的 J.-V.彭赛列于1839年首先论述了疲劳问题并提出“疲劳”这一术语。但疲劳研究的奠基人则是德国的A.沃勒。他在19世纪50～60年代首先得到表征疲劳性能的S-N曲线，并提出疲劳极限的概念。疲劳研究虽有百余年历史，文献极多，但理论不够完善。近年来，断裂力学的进展，丰富了传统疲劳理论的内容，促进了疲劳理论的发展。当前的发展趋势是把微观理论和宏观理论结合起来从本质上探究疲劳破坏的机理。
疲劳特征 疲劳破坏是一种损伤积累的过程，因此它的力学特征不同于静力破坏。不同之处主要表现为：①在循环应力远小于静强度极限（见材料的力学性能的情况下破坏就可能发生，但不是立刻发生的，而要经历一段时间，甚至很长的时间；②疲劳破坏前，即使塑性材料（延性材料）有时也没有显著的残余变形。
金属疲劳破坏可分为三个阶段：①微观裂纹扩展阶段。在循环加载下，由于物体内部微观组织结构的不均匀性，某些薄弱部位首先形成微观裂纹，此后，裂纹即沿着与主应力约成45°角的最大剪应力方向扩展。在此阶段，裂纹长度大致在0.05毫米以内。若继续加载，微观裂纹就会发展成为宏观裂纹。②宏观裂纹扩展阶段。裂纹基本上沿着与主应力垂直的方向扩展。借助电子显微镜可在断口表面上观察到此阶段中每一应力循环所遗留的疲劳条带。③瞬时断裂阶段。当裂纹扩大到使物体残存截面不足以抵抗外载荷时，物体就会在某一次加载下突然断裂。
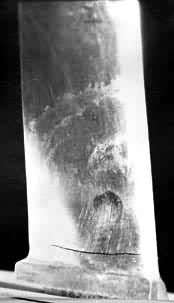
在疲劳宏观断口上往往有两个区域：光滑区域和颗粒状区域。疲劳裂纹的起始点称作疲劳源。实际构件上的疲劳源总是出现在应力集中区，裂纹从疲劳源向四周扩展。由于反复变形，裂纹的两个表面时而分离，时而挤压，这样就形成了光滑区域，即疲劳裂纹第二阶段扩展区域。第三阶段的瞬时断裂区域表面呈现较粗糙的颗粒状。如果循环应力的变化不是稳态的，应力幅不保持恒定，裂纹扩展忽快、忽慢或者停顿，则在光滑区域上用肉眼可看到贝壳状或海滩状纹迹的疲劳弧线 （图3）。
循环应力 疲劳破坏是在循环应力或循环应变作用下发生的。为了便于研究和分析疲劳问题，国际上对循环应力表示法已作出统一规定。循环应力的每一个周期变化称作一个应力循环。图4所示的恒幅循环应力由以下诸分量表示：①最大应力σ
，应力循环中最大代数值的应力，以拉应力为正，压应力为负。②最小应力σ
，应力循环中最小代数值的应力，以拉应力为正，压应力为负。③平均应力σ嚧，最大应力和最小应力的代数平均值，即σ嚧＝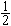
(σ
+σ
)。④应力幅σa，最大应力和最小应力的代数差的一半，即σa=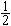
(σ
－σ
)。有些国家的文献将σa称作交变应力，但在中国常用交变应力一词表示循环应力。⑤应力变程σr，又称应力范围，是最大应力与最小应力之差，即应力幅的两倍。⑥应力比R，又称循环特征，是最小应力与最大应力的代数比值，即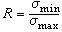
。R =－1的应力循环称为对称循环，其最大应力和最小应力绝对值相等，符号相反，且平均应力为零；R＝0的应力循环称为脉动循环，其最小应力为零；R等于其他值的应力循环称为非对称循环。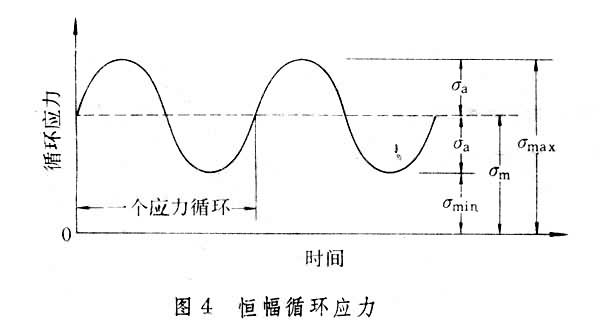
恒幅循环应变的表示法与此类似。
应力循环可以看成两部分应力的组合，一部分是数值等于平均应力σ嚧的静应力，另一部分是在平均应力上变化的动应力。在四个应力分量σ
、σ
、σa、σ嚧中只有两个是独立的。任意给定两个，其余两个就能确定。用来确定应力循环的一对应力分量σ
、σ
或σa、σ嚧称为应力水平。对恒幅循环应力，当给定R或σ嚧时，应力水平可由σ
或σa表示。产生疲劳破坏所需的循环数取决于应力水平的高低，破坏循环数越大，表示施加的应力水平越低。疲劳寿命 在循环加载下，产生疲劳破坏所需的应力或应变循环数称为疲劳寿命。对实际构件，疲劳寿命常以工作小时计。构件在出现工程裂纹以前的疲劳寿命称为裂纹形成寿命或裂纹起始寿命。工程裂纹指宏观可见的或可检的裂纹，其长度无统一规定，一般在0.2～1.0毫米范围内。自工程裂纹扩展至完全断裂的疲劳寿命称为裂纹扩展寿命。总寿命是二者之和。因为工程裂纹长度远大于金属晶粒尺寸，故可将裂纹作为物体边界，并将其周围材料视作均匀的连续介质，应用断裂力学方法研究裂纹扩展规律。
为了便于分析研究，常常按破坏循环次数的高低将疲劳分为两类：①高循环疲劳（高周疲劳）：破坏循环次数高于104～105的疲劳，一般振动元件、传动轴等的疲劳属此类。其特点是：作用于构件上的应力水平较低，应力和应变呈线性关系。②低循环疲劳(低周疲劳)：破坏循环次数低于104～105的疲劳，典型实例有压力容器、燃气轮机构件等的疲劳。其特点是：作用于构件的应力水平较高，材料处于塑性状态。很多实际构件在变幅循环应力作用下的疲劳既不是纯高循环疲劳也不是纯低循环疲劳，而是二者的综合。
相应地，裂纹扩展也分为高循环和低循环两类。高循环疲劳裂纹扩展规律可利用线弹性断裂力学方法研究；低循环疲劳裂纹扩展规律一般应采用弹塑性断裂力学方法研究，不过由于问题十分复杂，尚未很好地解决。
实践表明，疲劳寿命分散性较大，高循环疲劳尤其如此，因此必须进行统计分析，考虑存活（概）率(即可靠度)的问题。具有存活率p(如95％、99％、99.9％)的疲劳寿命Np的含义是：总体（母体）中有p的个体的疲劳寿命大于Np。而破坏（概）率等于(1-p)。 对应于高存活率或低破坏率的疲劳寿命，在设计上称为安全寿命。
疲劳问题范畴极为广泛。按材料性质及其工作环境划分，除一般金属疲劳外，还包括有非金属疲劳、高温疲劳、热疲劳（由循环热应力引起）、腐蚀疲劳、擦伤疲劳、声疲劳（由噪声激励引起）、冲击疲劳、接触疲劳等。金属疲劳寿命预估侧重于力学方面，并且是普遍关注的研究课题。为了进行疲劳寿命的理论估算和试验，首先必须了解材料的疲劳性能，以此作为理论计算的依据。其次，疲劳寿命的长短取决于所承受的循环载荷大小，为此还必须编制出供理论分析和全尺寸疲劳试验用的载荷谱。最后，根据材料的疲劳性能和载荷谱估算出疲劳寿命。以下分别加以介绍：
疲劳性能 材料抵抗疲劳破坏的能力。高循环疲劳的裂纹形成阶段的疲劳性能常以S-N曲线表征，S为应力水平，N为疲劳寿命。S-N曲线需通过试验测定，试验采用小型标准试件或实际构件。若采用小型标准试件，则试件裂纹扩展寿命较短，常以断裂时循环次数作为裂纹形成寿命。试验在给定应力比R或平均应力σ嚧的前提下进行，根据不同应力水平的试验结果，以最大应力σ
或应力幅σa为纵坐标，疲劳寿命N为横坐标绘制S-N曲线(图5)。表示寿命的横坐标采用对数标尺;表示应力的纵坐标采用算术标尺或对数标尺。在S-N 曲线上，对应某一寿命值的最大应力σ或应力幅σa称为疲劳强度。疲劳强度一词也泛指与疲劳有关的强度问题。为了模拟实际构件缺口处的应力集中以及研究材料对应力集中的敏感性，常需测定不同应力集中系数下的S-N曲线。对试验结果进行统计分析后，根据某一存活率p的安全寿命所绘制的应力和安全寿命之间的关系曲线称为p-S-N曲线。 50％存活率的应力和疲劳寿命之间的关系曲线称为中值S-N曲线，也简称S-N曲线。
当循环应力中的最大应力σ
小于某一极限值时，试件可经受无限次应力循环而不产生疲劳裂纹；当σ大于该极限值时，试件经有限次应力循环就会产生疲劳裂纹，该极限应力值就称为疲劳极限，或持久极限。如图5中S-N曲线的水平线段对应的纵坐标就是疲劳极限。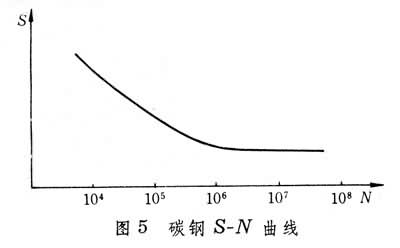
鉴于疲劳极限存在较大的分散性，人们根据现代统计学观点，把疲劳极限定义为：指定循环基数下的中值（50％存活率）疲劳强度。对于 S-N曲线具有水平线段的材料，循环基数取107；对于S-N曲线无水平线段的材料（如铝合金），循环基数取107～108。疲劳极限可作为绘制S-N曲线长寿命区线段的数据点。
根据各种应力比R或平均应力σ嚧的S-N曲线族，以应力幅σa为纵坐标，平均应力σ嚧为横坐标，还可绘出等寿命图（又称古特曼图）。图 6为钢材等寿命图。图中同一曲线上的各点表示具有相同寿命的σa和σ嚧值。各曲线汇交于横坐标轴上一点，该点σa为零；σ嚧等于静强度极限σb。
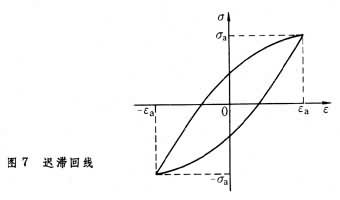
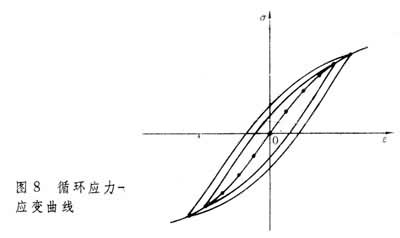
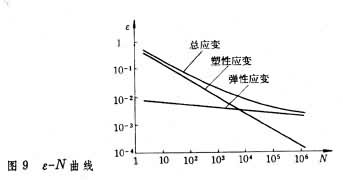
表征低循环疲劳裂纹形成阶段的疲劳性能的有ε-N曲线（即应变-寿命曲线）和循环应力-应变曲线，它们都是通过控制恒定的应变幅的试验测定的，所以低循环疲劳又称应变疲劳。试验采用无缺口光滑小试件。测试时，始终保持拉应变和压应变绝对值相等且为一常量。由于材料处于塑性范围，所以在恒定应变幅εa循环下应力幅σa不断发生变化。对于大多数材料，在达到疲劳寿命的一半之前，σa即趋于稳定，最后可得到一闭合的迟滞回线（图7）。对各个试件用不同的应变幅值进行试验，可得到不同大小的迟滞回线。将各回线上、下端点用曲线连接起来就得到循环应力-应变曲线（图8）。若将各试件一直试验到破坏并记录其疲劳寿命，以应变幅εa为纵坐标，疲劳寿命N为横坐标绘在双对数坐标纸上，则可得到ε-N曲线(图9)。总应变幅εa可分解为弹性应变分量和塑性应变分量，通常弹性应变-寿命关系和塑性应变-寿命关系在双对数坐标系中为两条直线。
对于高循环疲劳裂纹扩展，大量试验结果表明，疲劳裂纹扩展率
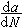(每一应力循环的裂纹扩展量)与应力强 度因子变程ΔK的关系在双对数坐标系中如图10所示。其中a为裂纹长度，ΔK＝K
－K
，K
和K
分别为对应最大应力σ
和最小应力σ
的应力强度因子(见线弹性断裂力学)。由图10可见，裂纹扩展分为三个阶段。对于阶段I，当ΔK降低至某一极限值ΔKth时，裂纹基本不再扩展，该值称为疲劳门槛值。它受平均应力、环境和材料的微观结构等因素影响较大。对于裂纹扩展阶段Ⅱ，美国的P.C.帕里斯于1963年根据试验结果提出一个公式，后称为帕里斯公式：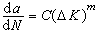 
，式中C和m为材料常数。对于一般常用结构钢铝合金，m＝2～4。帕里斯公式在双对数坐标系中为一直线，与阶段Ⅱ的试验结果基本符合。裂纹扩展的最后阶段Ⅲ的机理比较复杂，在裂纹扩展寿命中所占比例甚小，研究也较少。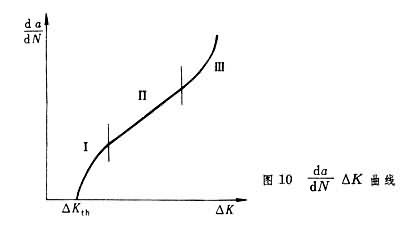
在变幅循环应力作用下，先行的高峰应力循环对后继的低应力循环的裂纹形成和裂纹扩展的影响，称为过载效应。对于带有缺口或含裂纹的构件，在预先施加高峰拉应力后，在缺口处或裂纹尖端形成塑性区，产生有利的残余压应力，故可延长疲劳寿命。
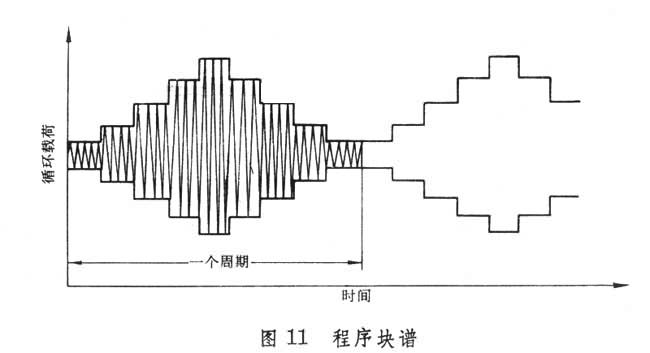
疲劳载荷谱 结构或零件所承受的循环载荷实际上为一连续的随机过程。为了便于进行全尺寸疲劳试验和寿命估算，根据实测载荷数据编制出的模拟实际情况的载荷－时间历程称为载荷谱。产品疲劳寿命理论估算和试验结果的可靠性在很大程度上取决于载荷谱的真实性。载荷数据常常借助应变仪或过载计数仪等来测定。将实测载荷数据简化为一系列全循环或半循环的过程称为计数法。载荷谱的编制与所采用的计数法有关。国际上使用的计数法有十多种，早期使用的有峰值法、穿级法和变程法等。目前一般趋向于使用雨流法或变程对均值法。20世纪60年代以来，大多编制程序块谱（图11）。它的每一周期由若干级不同大小的恒幅载荷循环或恒幅应力循环组成，同一级的载荷循环称为一个程序块。每一周期内的程序块按一定图案排列，图11中程序块属于低-高-低序列。按周期逐次重复地施加载荷即所谓程序加载。为了更好地模拟实际情况，目前正研制一种按任务阶段划分的伪随机谱。在产品的预设计期间，为了预估疲劳寿命，载荷谱可取自有关规范，或者根据使用条件由理论计算导出。
累积损伤理论 累积损伤理论提供了在程序加载或变幅加载下构件寿命估算的方法和依据。累积损伤理论至今虽有数十种，但应用最广的仍属最早提出的线性累积损伤理论，其内容如下：
设一个循环周期内含有k级应力水平σ1，σ2，…，σk，各级应力水平的循环数分别为n1，n2，…，nk。令N1，N2，…，Nk分别表示在各级应力水平单独作用下的疲劳寿命（可由S-N曲线查得）。累积损伤理论认为：疲劳损伤度可用相应的循环比即n1/N1，n2/N2，…，nk/Nk表示。如以T表示周期数，则在整个工作期间各级应力水平对构件所造成的损伤度分别为：
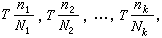当损伤度总和累积至1(100％)，即
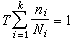时，构件即发生破坏。线性累积损伤理论由J.V.帕姆格伦和M.A.迈因纳分别于1942年和1945年各自独立提出。这一理论未考虑应力水平先后次序的影响，也未计及过载效应、欠应力(低于疲劳极限的应力)等影响，常常与试验结果相差很大，尚待进一步研究。但计算公式简便、直观，故在估算寿命时仍被广泛采用。
对于裂纹形成寿命的估算，一般采用名义应力法和局部应力应变法。名义应力法在应用累积损伤理论时，依据构件的S-N 曲线或与构件应力集中系数相同的材料的S-N 曲线计算损伤度。而局部应力应变法先对缺口根部进行应力应变分析，然后依据无缺口光滑小试件的ε-N 曲线，计算每一循环的损伤并进行累积，进而给出寿命。另外，用于螺栓或铆钉连接件寿命估算的应力严重系数法，也基于具有应力集中的材料的S-N曲线。
估算裂纹扩展寿命，须先求出构件应力强度因子，以得到ΔK。再将帕里斯公式作适当修正后，利用数值积分法，即可求得由初始裂纹扩展至临界裂纹或断裂的寿命。
参考书目
T.V.Duggan and J.Byrne，Fatigue as α DesignCriterion，Macmillan，London，1977.
A Guide for Fatigue Testing and the Statisti-calAnalysis of Fatigue Data，ASTM STP91A， Fatigue Committee of American Society for Testing Mate-rials，1964.
H.O.Fuchs and R.I.Stephens， Metal Fatigue in Engi-neering，John Wiley & Sons，New York，1980.
中村宏、田中真一著：《機械の疲れ寿命算出法》，養賢堂，東京，1976。