松弛法(卷名:数学)
relaxation method
数值计算中解线性代数方程组的一类迭代法。当方程组的未知量个数甚多而又有大量的零系数时,常用这类方法求解。
基本迭代格式 设线性代数方程组为
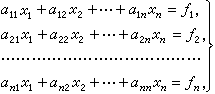 (1)此处x1,x2,…,xn为未知量,αij(i,j=1,2,…,n)和ƒ1,ƒ2,…,ƒn为已知量,又设αii(i=1, 2,…, n)均不为零,则由迭代公式
(1)此处x1,x2,…,xn为未知量,αij(i,j=1,2,…,n)和ƒ1,ƒ2,…,ƒn为已知量,又设αii(i=1, 2,…, n)均不为零,则由迭代公式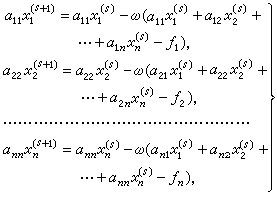 (2)和给定的初值x
(2)和给定的初值x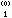 ,x
,x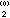 ,…,x
,…,x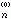 ,就可求出x
,就可求出x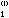 ,x
,x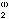 ,…,x
,…,x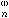 ,由后者又可求出x
,由后者又可求出x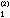 ,x
,x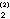 ,…,x
,…,x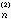 ,如此继续直到满足精度要求为止,例如对所有的i,
,如此继续直到满足精度要求为止,例如对所有的i,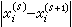 或
或 (若
(若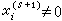 )或剩余
)或剩余 的绝对值|
的绝对值|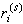 |小于某给定的小数ε时就终止迭代而将
|小于某给定的小数ε时就终止迭代而将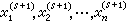 取作方程组(1)的解。迭代格式(2)称为同时超松弛法或JOR法,其中的ω为一实参数,称为松弛因子,当ω=1时就是通常所谓的简单迭代法,或称雅可比法。
取作方程组(1)的解。迭代格式(2)称为同时超松弛法或JOR法,其中的ω为一实参数,称为松弛因子,当ω=1时就是通常所谓的简单迭代法,或称雅可比法。若在迭代格式(2)中,将第i个方程迭代出的
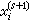 的值代替其后各方程中的
的值代替其后各方程中的 ,就得到迭代格式
,就得到迭代格式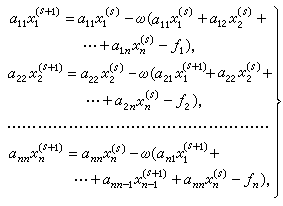 (3)它称为逐次超松弛法,或SOR法,一般所说的超松弛法就是指这种方法,当ω=1时称为高斯-赛德尔法或赛德尔法,有时将ω >1的情形称为超松弛法,而将ω <1的情形称为亚松弛法或低松弛法。迭代格式也可用矩阵形式来写,设
(3)它称为逐次超松弛法,或SOR法,一般所说的超松弛法就是指这种方法,当ω=1时称为高斯-赛德尔法或赛德尔法,有时将ω >1的情形称为超松弛法,而将ω <1的情形称为亚松弛法或低松弛法。迭代格式也可用矩阵形式来写,设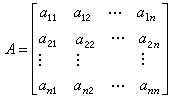 (4)为n阶方阵,
(4)为n阶方阵,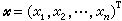 ,
,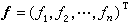 为n维列向量,则(1)可写为
为n维列向量,则(1)可写为 (5)记A的对角线元素所成的对角矩阵为D,又B=D-A,则(2)可写为
(5)记A的对角线元素所成的对角矩阵为D,又B=D-A,则(2)可写为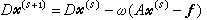 (6)或
(6)或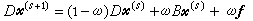 , (7)再设L和U分别为B的下三角形和上三角形矩阵,则A=D-L-U,而(3)可写为
, (7)再设L和U分别为B的下三角形和上三角形矩阵,则A=D-L-U,而(3)可写为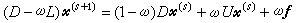 。 (8)
。 (8)收敛性 迭代格式(7)和(8)可统一地写为
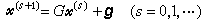 (9)的形式,其中G称为迭代矩阵,对应于(7)和(8)分别有G=D -1[(1-ω)D+ωB]和G=(D-ωL)-1[(1-ω)D+ωU]。 以ρ(M)表示方阵M的谱半径,其定义为M的按模最大特征值的模,则迭代过程(9)收敛的充分必要条件为
(9)的形式,其中G称为迭代矩阵,对应于(7)和(8)分别有G=D -1[(1-ω)D+ωB]和G=(D-ωL)-1[(1-ω)D+ωU]。 以ρ(M)表示方阵M的谱半径,其定义为M的按模最大特征值的模,则迭代过程(9)收敛的充分必要条件为ρ(G)<1。 (10)由此可得收敛的一个充分条件为这里‖G‖是G的任意一
‖G‖<1 , (11)种范数。对上面松弛法的迭代格式可以得出一些有关收敛性的命题如下:
① 若A为严格对角优势矩阵(见对角优势矩阵)或不可约弱对角优势矩阵,|D -1B|为矩阵D -1B的元素取绝对值所成的矩阵,则JOR法和SOR法在
0<ω<2/(1+ρ)|D -1B|范围内收敛,并且在所述条件下,上式右端是一个大于1的数;
② 若A为埃尔米特矩阵,且αii(i=1,2,…,n)均为正,则JOR法收敛的充分必要条件为A和2ω -1D-A正定;
③ SOR法收敛的必要条件为0<ω<2;
④ 若A为埃尔米特矩阵,αii(i=1,2,…,n)均为正,则SOR法收敛的充分必要条件为A正定和0<ω<2。
松弛因子的选取 ω 的值选取得适当可使松弛法有较好的收敛性,然而如何选取最优的ω,还是一个困难的问题。通常用五点差分格式解二维二阶椭圆型方程得到的线性代数方程组的系数矩阵是块三对角矩阵,主对角块是三对角阵,非主对角块为对角阵。对这种方程组若记简单迭代和超松弛迭代的迭代矩阵为J和Lω,则它们的特征值λ(J)和λ(Lω)之间有关系
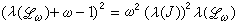 。 (12)由此可以研究ω 的选取问题,例如可以证明:在上述情形下使超松弛迭代收敛最快的松弛因子为
。 (12)由此可以研究ω 的选取问题,例如可以证明:在上述情形下使超松弛迭代收敛最快的松弛因子为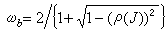 。 (13)此时
。 (13)此时 , (14)这里ρ(J)和ρ(
, (14)这里ρ(J)和ρ(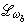 )分别为矩阵J和
)分别为矩阵J和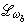 的谱半径。这些结果还可推广到所谓“相容次序”的矩阵。尽管如此,在实际计算中仍难以精确确定ωb的值,而往往是通过一些试算或用其他方法先估计ρ(J),再来估计ωb。也可用若干ω值试迭代,从中选取使敛速较快者。从(12)式还可看出,ωb在1与2之间,且从大于ωb的一侧选取ω,然后逐步减小,较为有利。
的谱半径。这些结果还可推广到所谓“相容次序”的矩阵。尽管如此,在实际计算中仍难以精确确定ωb的值,而往往是通过一些试算或用其他方法先估计ρ(J),再来估计ωb。也可用若干ω值试迭代,从中选取使敛速较快者。从(12)式还可看出,ωb在1与2之间,且从大于ωb的一侧选取ω,然后逐步减小,较为有利。当取ω=1时,由(12)有λ(L1)=(λ(J))2。即对相容次序的矩阵来说,赛德尔迭代比简单迭代敛速快一倍。在很多情况下,赛德尔迭代比简单迭代收敛快。实际上,若A =M-N,且A -1、M -1和N的元素均非负,则迭代过程
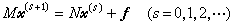 (15)收敛,且N 的元素愈少愈小,收敛愈快。不难看出,前述的迭代格式都是(15)的特殊情形,并且赛德尔迭代较之简单迭代相应的N 的元素要少得多,从而收敛也要快些,当然在不满足这些条件的情况之下,也可能出现相反的情形。
(15)收敛,且N 的元素愈少愈小,收敛愈快。不难看出,前述的迭代格式都是(15)的特殊情形,并且赛德尔迭代较之简单迭代相应的N 的元素要少得多,从而收敛也要快些,当然在不满足这些条件的情况之下,也可能出现相反的情形。此外,若将A分成块来形成分块矩阵,而将(6)(7)(8)中的D、B、L和U分别取为A的主对角块、-A的非主对角块、下三角块和上三角块所形成的矩阵,则迭代(15)的收敛速度可能更快。这样得出的迭代格式称为块松弛迭代,相应地有块简单迭代,块超松弛迭代等。对照之下,前面的迭代就称为点松弛迭代,上面关于最佳松弛因子的讨论对块松弛迭代也是适用的。
上述的一些迭代法有时收敛都很慢,这就需要用一些辅助方法来加速收敛,例如半迭代加速、共轭梯度法加速等。
参考书目
冯康等编:《数值计算方法》,国防工业出版社,北京,1978。
D.M.Young,Iterative Solution of large Linear Systems,Academic Press, New York,1971.
R.S.瓦格著,蒋尔雄、游兆永、张玉德译:《矩阵迭代分析》,上海科学技术出版社,上海,1966。(R.S.Varga,Matrix Iterative Analysis , Prentice - Hall,Englewood Cliffs, New Jersey, 1962.)