样本(卷名：数学)
sample
又称子样。按一定方式从总体中抽取的若干个体，用于提供总体的信息及由此对总体作统计推断。用样本对总体作推断时，常利用样本的某个或某些特定的函数，例如样本均值、样本方差、样本极差等。这种不包含总体分布中任何未知参数的样本函数称为统计量，用样本推断总体，常通过统计量来实现。
若样本由n个个体x1，x2，…，xn所组成，则可把样本记为尣＝(x1，x2，…，xn)或简记为尣 。n称为样本大小或样本容量。样本尣所能取的一切值的集合H称为样本空间。
从总体中抽取样本的过程叫抽样。最常用的抽样方式是简单随机抽样，按这种方式抽样，总体中的每个个体都有同等的机会被抽入样本，且每次抽出的个体，在记下其指标后，还要放回总体中去，以保证在下次抽取时每个个体仍有与第一次抽取时同等的机会被抽入样本，这样得到的样本称简单随机样本，也简称随机样本或简单样本。简单随机抽样的具体结果x1，x2，…，xn是一组确定的值，但它是随每次抽样而改变的，因此每个xj可看作是描述总体的随机变量 x的一次观测值，一个随机样本又可记为X=(x1，x2，…，xn)，式中xj是相互独立且都与总体分布相同的随机变量，故尣是一个n维的随机向量。它的分布称为样本分布。
样本来自总体，包含有总体的信息。但它本身只是一堆数据，只有经过适当的加工整理，才能将所需要的信息提取出来。整理的方法有二：一是将样本数据分组并表示成图表；二是计算有关的统计量。
当样本取离散数值，即只能取有限多个或可数多个数值时，则可按这些数值自然分组。当样本可在某取值范围内连续取值时，则可将其实际取值范围划分成 m个区间，亦即m个组；设第i组的端点为
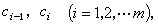可以规定组的划分为(сj-1，сj]或[сj-1，сj)。区间长度hj称为组距，通常取为相等的。分组确定后，即可计算样本数据落入每组的个数（即频数）nj，及它在数据总数n中所占的比（即频率）
。将上述数值列成表格，即得样本的频数（频率）分布表。例如，在机床上加工一零件，随机地抽取100只，测得其某指标值如表1。
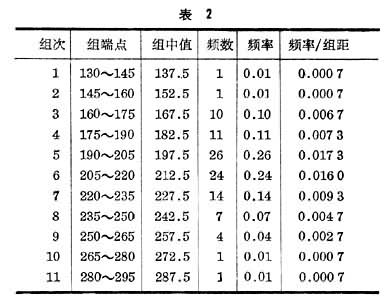
经过整理得频数（频率）分布表如表2。表中的组距h=15。为了醒目，常将上述的频数（频率）分布表用频率直方图的形式形象地表示出来。其作法是：在数轴上标上с0， с1，…， сm，以每组的区间(сj-1，сj)为底，以频率/组距的值为高作矩形，这m个矩形构成的图形称为频率直方图。由表1 作出的频率直方图见下图
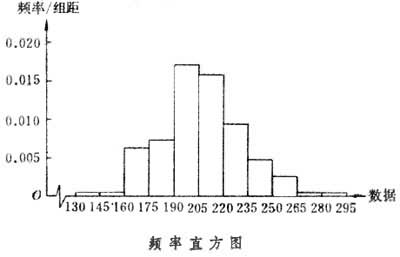，图中每个矩形的面积即是相应组的频率，而m个矩形的面积之和等于 1。频率直方图可用作总体分布密度函数的一种估计。在作频率直方图时，必须适当决定分组数目m、分组区间和第一个组的左端点 с0。一般说来，并无硬性规定。通常只要使得数据分散在组中而不偏向组内一边就行了。组数m，一般以十几个到二十几个为宜，太少会掩盖各组内数据变动情况，太多又体现不出总体分布的规律性。分组法的缺点在于分组区间及分组数目的多少因人而异，而利用经验分布函数就没有这个缺点。经验分布函数Fn(x)定义为x1，x2，…，xn中小于x的个数与n之比，－∞<x<∞，它是一个阶梯函数，且具有通常分布函数的性质。Fn(x)是总体分布函数F(x)的一个比较良好的估计。可以证明，若 x1， x2，…，xn是从总体中抽取的简单随机样本，则当n→∞时，Fn(x)在全直线(-∞，∞)上几乎必然一致收敛于总体分布函数F(x)。