样条函数(卷名：数学)
spline function
一类分段（片）光滑，各段（片）交接处具有一定光滑性的函数，简称样条。样条函数的名称来源于船体放样时用来画光滑曲线的机械样条──弹性的细长条。它产生的背景是离散数据的处理。高次多项式插值过程有数值不稳定的缺点，而利用分段低次多项式，在分段处具有一定光滑性的函数插值过程有较好的稳定性和收敛性，这种插值过程产生的函数就是（多项式）样条函数。20世纪60年代中期，它与计算机辅助几何设计相结合，在外形设计（汽车、飞机等）方面得到了成功的应用。同时，样条理论研究亦逐步深入，后被作为函数逼近的有力工具。其应用亦逐渐扩展到各类数据的插值、拟合与平滑、数值微分与积分、微分方程和积分方程的数值解等方面。从1964年起开始研究非多项式样条，样条的概念有了许多扩展。它同其他数学分支，诸如最优控制、多点变分问题、多点边值问题、广义逆算子、统计计算、计算几何、泛函分析以及多点弹性平衡问题等有密切联系。
下面是几种常用的样条函数。
三次样条 应用很广的一类样条函数。给定区间[α，b]的一个分划
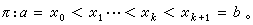若函数S(x)在每一个子区间[xj，xj+1](i＝0，1，…，k)上是三次多项式，在交接点x1，x2，…，xk处有二阶连续导数，便称它是定义在[α，b]上关于分划π的三次(或四阶)样条函数，简称三次样条。x1，x2，…，xk称为样条结点。三次样条函数可表成 
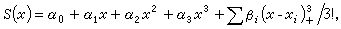式中记号
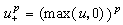。三次样条的力学模型是弹性细梁在结点xj处受强度为 βj的集中力作用而产生的小挠度曲线。三次样条起源于函数插值，是函数逼近的有效工具。 它具有许多最佳性质。 例如， 满足插值条件
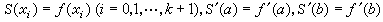，的三次样条S(x)存在、惟一且在一切满足上述插值条件的二次连续可微函数类中使
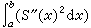取极小。 当ƒ∈C4[α，b]时可得到余项估计
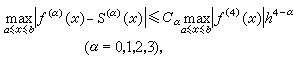式中Cα为与ƒ无关的常数;
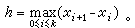又如，三次样条还是下述平滑问题的解；设ρ>0为给定权因子，{yi}为给定数据，求S∈H2[α， b]，且使
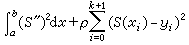取极小的解。它也是凸集逼近问题：求 
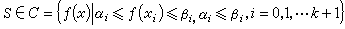使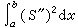
取极小的解。三次样条的上述最佳性质，都可推广到奇次样条。多项式样条 如果函数S(x)在
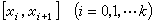上是m-1次多项式，在xj处有直到m-rj-1阶的连续导数，而m-rj阶导数在xj处有跳跃性间断，这里
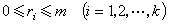便称S(x)为以xj为rj重结点的m-1次(或m 阶)样条。结点xj的重数不超过rj的m-1次样条可表为
…+
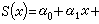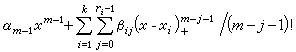。这种样条的集合作成n=m +r1+…+rk维线性向量空间。m为偶数的奇次（偶阶）样条，具有三次样条的许多类似的最佳性质。当m=3，r1=r2=…=rk=1时，便得到二次单结点样条，即抛物样条。它是偶次样条的代表，有许多不同于三次样条的性质。用它作插值时，宜用样条结点的中点
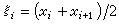作插值结点。多项式样条即分段多项式，能靠增加结点数目或提高结点重数来增加样条空间的维数。它既有低次多项式的简单性，又有相当的光滑性和灵活适应性，还避免了高次多项式插值的不稳定性，是函数逼近的重要工具。
多项式B样条 设
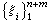为单调不减序列且
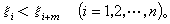将函数
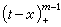关于t以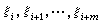
为结点作m阶差商再乘以
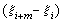，得一函数Bj，m(x)，称为以
…，
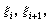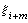为结点的m 阶B 样条。它可以形式地看作对δ 函数δ(t-x)关于t积分m次，再对t作m阶差商并乘以
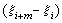的结果。它形如山丘，有许多类似δ函数的性质，如局部非零且非负，即当x∈
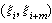时，Bj，m>0;否则，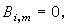
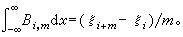若在序列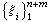
中结点xj出现rj次(j=1，2，…，k)，又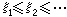
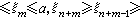
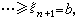则相应B样条系
构成上面定义的[α，b)]上m阶多项式样条空间的基底。它说明了B样条名称的由来。B 样条在样条理论和计算中，特别是在构造平滑公式中起着基本的作用。基样条 以整数
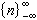或将它们平移1/2的半整数点为样条单结点的m 阶样条，称为m 阶基样条，它对函数插值很有用。基样条可表为 
其中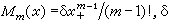
为以1为步长的对称差分算子。基样条插值问题S(n)=yn(n=0，±1，…)，当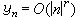
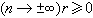为某常数时，其解存在、惟一，且有|S(x)|=O(|x|r)(|x|→∞)。平滑问题
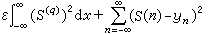取极小，其中ε为正常数，yn为给定值，其解是2q阶样条。在 B样条和基样条的基础上还发展了诸如切比雪夫样条、L样条或微分算子样条、指数样条等样条函数。三次样条是在小挠度的假设下得到的，为了处理大挠度问题，常用参数样条。此外，还建立了种种非线性数学模型，发展了诸如圆弧样条和有理样条等，它们在实际应用上也很重要。