原子轨道(卷名：化学)
atomic orbital
描述原子中单电子处于真实的（如氢原子或类氢离子的单电子体系）或假定的（即有效的，如多电子原子的电子体系）中心势场中束缚态波函数的空间部分，即单电子薛定谔方程
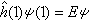（1)的解ψ(1)称原子轨道。式中
，为单电子哈密顿算符；
，为约化质量；
，h是普朗克常数；墷2是拉普拉斯算符；m、Μ分别是电子和原子核的质量。在直角坐标系中，
，V(r1)是单电子真实的或假定的有效势函数，仅仅是电子与核的距离r的函数，与方位(θ，φ)无关。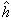
(1)和ψ(1)中的数字1表示单电子空间坐标（以核为参考点）。由于中心场中的单电子哈密顿算符
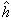(1)、角动量二次方算符
以及角动量算符在z 轴上的投影
，i为
。这三个算符彼此互易，构成力学量的完全集合
，所以 ψ(1)由三个守恒量εnl（能量）、l(l+1)啚2（角动量二次方）和 m啚（角动量的z分量）确定。也就是说，ψ(1)是下述三个方程的共同本征函数：
(1)
(2)
(3)式中n为主量子数，l为角量子数，m为磁量子数。氢原子和类氢离子的原子轨道 氢原子和类氢离子是由一个电子和原子核组成的双粒子体系，原子核带Ze正电荷，Z为原子序数。其库仑相互作用位能只与电子和核的相对位置 |r|＝|re-rN|有关，re为电子位矢，rN为核位矢。引入质心坐标以后，双粒子运动方程可分成两个分别描述质心的自由运动和电子相对于核的相对运动的方程：
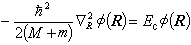(4)
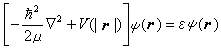(5)式中墷嵔表示相应于质心坐标的拉普拉斯算符；R是质心位矢，Ec是质心运动能量，这是个自由粒子运动方程，与原子内部结构无关。式(5)中r是电子相对于核的位矢;E是电子相对于核运动的能量，即电子的能级。这样，双粒子问题简化为单粒子问题。方程 (2)、(3)、(5)的共同本征函数的数学表示式和本征值为：
(6)式中n＝1，2，3，…；
为氢原子第一玻尔半径。
(7)式中l＝0，1，2，…，n-1；m＝0，±1，±2，…，±l；Rnl(r)是原子轨道的径向部分；Ylm(θ，φ)是球谐函数，即原子轨道的角度部分。 Rnl(r)和Ylm(θ，φ)的物理意义是：规定ωnl(r)dr为电子在r→r+dr球壳内的几率，则：
同样，在方位(θ，φ)附近立体角元dΩ ＝sinθdθdφ内的几率
。图1是径向分布图像(图中的10、20、…为量子数，如10表示n＝1、l＝0)，角分布图象见图2。
多电子原子轨道 由于多电子体系中存在着电子间相互作用，运用了核电分离的近似后，还不能精确求解体系的薛定谔方程。常进一步采用中心势场近似方法，即认为某个电子处于原子核和其他电子产生的平均势场中运动，并在对方位(θ，φ)取平均以后，使该电子的位能函数只依赖于电子对核的距离r，记作V(r)。根据电子受核的静电作用受到其他电子的屏蔽，可假定V(r)能写成：
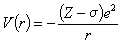(8)式中 σ为其他电子引起的屏蔽常数。这样，多电子原子轨道将具有与类氢离子的轨道相似的形式，仅是用(Z-σ)代替了原来类氢轨道的 Z而已。若中心势场V(r)不具有式(8)所示形式，多电子原子轨道的径向部分Rnl(r)将不同于类氢轨道（但角度部分是完全相同的），且轨道能量εnl 也将与角量子数l有关。n相同时，l越大，轨道能量εnl 越高。实际上，多电子原子轨道常用自洽场方法求解单电子函数满足的哈特里－福克方程(见自洽场分子轨道法)获得。自洽场原子轨道能够给出多电子原子的电子结构方面足够精确的信息，因而至今哈特里－福克自洽场方法仍被广泛采用。