流形上的偏微分算子(卷名：数学)
partial differential operator on manifold
定义在整个微分流形上的偏微分算子。在一个未知函数的情形，m 阶线性的偏微分算子是M上C∞函数的集合C∞(M)到C∞(M)的一个线性映射l，而在每一坐标区域中，l可表示为
这里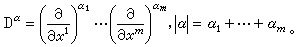
显然，在两个坐标区域的重迭部分，l的两种表示可以通过坐标变换互相转换。例如，黎曼流形上的第二类贝尔特拉米算子，在每一个坐标区域中可表示为
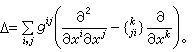这里gij(x)是度量张量的反变分量，
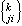是克里斯托费尔符号（见黎曼几何学）。多个未知函数的线性偏微分算子 l可定义如下：设
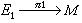是定义在M上的向量丛，Г(E1)为C∞截面的全体，同样Г(E2)表示另一向量丛
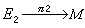的C∞截面的全体，l是Г(E1)到Г(E2)的线性映射，它满足：对每一小的坐标区域U，如果Г(E1)和Г(E2)中的元素在U上的限制可以用m1元和m2元的列向量函数来表示，则l可以写为
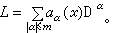这里αα(x)是m2×m1阵，m1和m2分别是E1和E2的纤维的维数。在局部坐标下，微分算子的主符σ(l)(ξ)可表示为
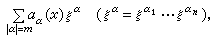偏微分算子的类型可由其主符（和通常偏微分算子一样地）来决定。特别，对任何ξ≠0，若 σ(l)(ξ)恒为非异方阵时，算子l就是椭圆型的，例如，第二类贝尔特拉米算子Δ的主符可表示为
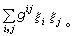由于黎曼度量是正定的，所以Δ是椭圆算子。对算子l而言，可以定义其象
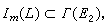其核ker(l)= {u∈Г(E2)，lu=0}，还可以作余核 Coker(l)=Г(E2)/Im(l)，它们都是线性空间。当l是椭圆型偏微分算子时，可以证明Ker(l)和Coker(l)都是有限维的，Ker(l)的维数减去 Coker(l)的维数称为算子l的指标。20世纪60年代，M.F.阿蒂亚和I.M.辛格得到著名的指标定理:椭圆算子l的指标是由向量丛E1、向量丛E2和主符σ(l)所确定的一个拓扑不变量。在微分几何中时常要求解由微分算子所定义出来的偏微分方程，这种方程的解是否存在，有多少，往往不仅依赖于方程本身，而且依赖流形的性质。例如贝尔特拉米-拉普拉斯方程
Δ u＝0在紧致流形上就只有常数解。
在微分流形中也可以定义非线性的偏微分方程，其重要性也与日俱增，极小曲面方程，蒙日-安培方程、杨-米尔斯方程都是非线性的偏微分方程。