电感(卷名：物理学)
inductance
表达时变电流在电路内部或邻近电路中产生感应电动势的基本电路参数。电感与电容、电阻共同决定电路的功率因数、瞬变过程、稳定状态、电振荡性质等等。
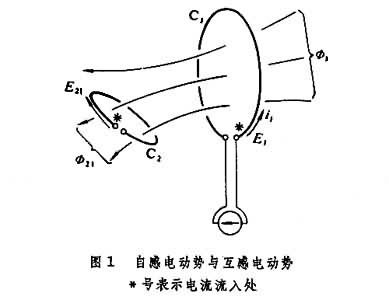
时变电流i1通过C1电路时，产生时变磁通φ1(图1)，其一部分φ21被邻近的C2电路所围，叫做互磁通。根据法拉第电磁感应定律，在两电路中分别产生自感电动势和互感电动势，即
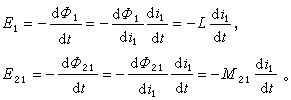比例系数L叫做电路C1的自感;M21叫做电路C2与C1的互感。如果电路的大小、形状、位置都不变，且周围媒质的导磁率μrμo与磁场强度无关，则L及M21都是常数
(1)自感与互感统称电感，式(1)是电感的基本定义式。电感的国际制(SI)单位为亨(H)。图1中，如果导电回路C2为n2匝的集总线圈，每匝所围磁通各等于φ21，则线圈 C2各匝所围磁通的总和为n2φ21＝ψ21，产生n2倍的感应电动势。ψ＝nφ称为磁链，单位为韦匝，简作韦。
多匝线圈的电感定义为
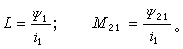(2)如果回路C1及C2分别为n1及n2匝的集总线圈，而其他给定的条件不变，则自感正比于匝数的二次方，互感正比于两线圈匝数之积。计算互感的诺埃曼公式 根据在均匀、线性磁介质中的一对理想细导线回路C1与C2(图2)的几何参数，可用诺埃曼公式计算互感
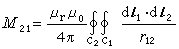。 (3)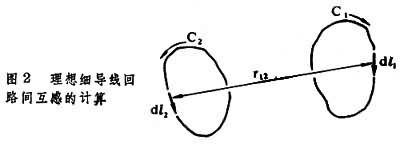
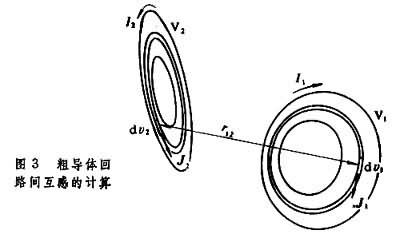
如果C1与C2为粗导体回路，见图3，并且导体的磁导率与其周围空间均匀线性媒质的相等，则诺埃曼公式修改为
， (4)式中J1dv1及J2dv2是两导体V1及V2内部任意微电流管的电流元，I1及I2是各导体传导的总电流。因为两个回路的积分次序可以颠倒而式(3)或式(4)的值不变，故M21＝M12=M，即互感具有倒易性〔当磁介质不均匀时，这种倒易性仍存在，但(3)(4)两式在媒质非均匀时不成立〕。互感的倒易性表明:第1回路传载电流i时，在第2回路产生的互磁链ψ21，等于第2回路传载相同的电流i而在第1回路产生的互磁链ψ12；当两个回路中通过相同的时变电流时，两个互感电动势的数值相等。
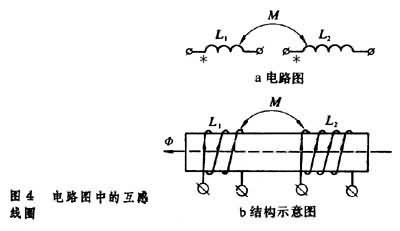
M值的正负取决于式(3)或式(4)在两回路中选择的积分方向（电磁感应定律表明），当两个互感电路的参考方向都与互磁通的参考方向成右手螺旋关系时，M为正值。在电路图中，互感的两线圈的符号旁各有一端标明极性，当电流的参考方向同由标记端进入时，M为正。图4a为互感的电路图例，4b为相应的结构示意图。写互感元件的伏安关系式，或用基尔霍夫电路定律建立电路方程时，都要根据极性标记及参考方向决定互磁通、互感电动势或电压的代数值的正负号。
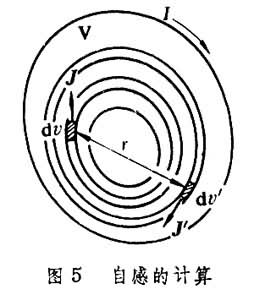
计算自感的诺埃曼公式 若两个粗导体回路完全重合，即V1＝V2＝V 及I1＝I2＝I，如图5所示，并设导体与其周围均匀媒质的磁导率都等于常数μrμo，这时计算自感的诺埃曼公式为：
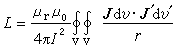(5)式中Jdv及J′dv′为惟一的导体回路 V内部的两个电流元。计算自感时不可忽略导线的截面积，因为理想细导线的自感等于无穷大。但是，如果圆导线截面尺寸远小于回路尺寸，见图6，可以用近似公式计算其自感
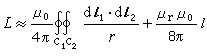， (6)式中C1是细导体的轴线，dl1是轴线的长度元；C2是沿着回路依附于细导体表面上内侧的闭合曲线，dl2为该曲线的长度元。式(6)中的双重线积分项代表导体外部的磁通与整匝导线相链的部分电感，叫做外自感；式中后一项代表圆柱形导体内部的磁通产生的部分电感，叫做内自感。内自感正比于导线的长度 l和导线材料的磁导率μrμo，而与导线的半径无关。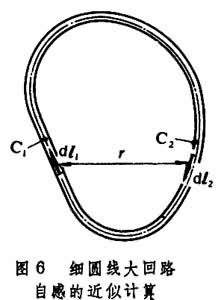
有互感线圈的串联和并联 有互感的一对线圈有两种串联方式，得到的总电感不相等。图7a为顺向串联，电流通过两线圈时产生加强的磁场，总电感为
L＝L1＋L2＋2M。图7b为反向串联，电流通过时产生相消磁场，总电感为
L＝L1＋L2－2M。
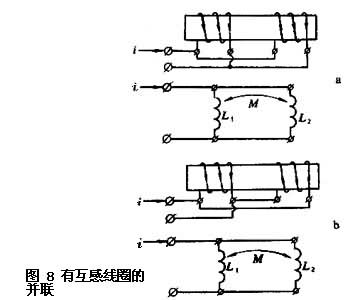
并联也有两种方式，得到不等的总电感，图8a中，两线圈产生加强的磁场，总电感为
L＝(L1＋L2－M2)/(L1＋L2－2M)。图8b中，两线圈产生相消的磁场，总电感为
L＝(L1＋L2－M2)/(L1＋L2＋2M)。
两线圈间磁耦合的紧密程度用耦合系数
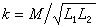表示，式中L1与L2为各线圈的自感，M为它们的互感。
参考书目
冯慈璋主编:《电磁场》，人民教育出版社，北京，1979。
W.R.Smythe，Static and Dynamic Electricity，2nd ed.，McGraw-Hill，New York，1950.